概要

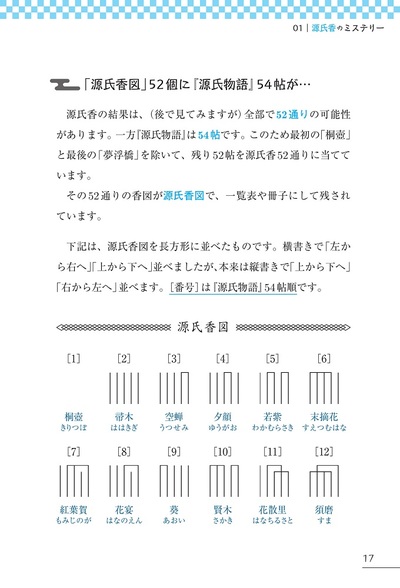
関孝和がベルヌーイ数を発見していたことは特に有名ですが，和算家が大きく貢献した有名な数が他にもあります。関孝和の孫弟子にあたる松永良弼（よしすけ）によるベル数や，坂正永（まさのぶ）によるスターリング数などです。和算家たちはこれらの数を「場合の数」と捉えます。一方，スターリングなど西洋の数学者たちは「代数」と捉えていました。スターリング数は，ベルヌーイ数に関する重要なクラウゼン-フォンシュタウトの定理に欠かせない重要な数でもあります。和算と西洋数学によるそれらの数の捉え方の違いを通して，それらがどのようにしてベルヌーイ数へとつながっていくのか，わかりやすく解説します。題材として「源氏香図」を使います。これは単なるデザインではなく，数学的な意味をもつもので，源氏香52通りはベル数とも呼ばれています。

楽しみながら数学を学ぶことができる1冊です。

こんな方におすすめ

• 和算と西洋数学のつながり，離散数学，組み合わせ数学に興味がある人
• 和算家が関わった有名な数を知りたい人など

サンプル

目次

• はじめに

1章　源氏香のミステリー

• 日本発の研究とは…
• 「源氏香図」52個に『源氏物語』54帖が…
• 「源氏香」から和算家達が発見した式とは…
• 「二項係数」を並べて「パスカルの三角形」を作ろう
• 「源氏香図」52個を描き上げよう
• 源氏香図のミステリー（1）
• コラム①10種香は何通りか（1）

2章　和算家のスターリング数

• 和算家達のさらなる発見とは…
• 漸化式から「第2種スターリング数の三角形」を作ろう
• 「n＝4の香図」を描き上げよう
• 源氏香図のミステリー（2）
• 漸化式から「第1種スターリング数の三角形」を作ろう
• 「置換」を「プレゼント交換」で見てみよう
• 「置換」を「サイクルの個数」で見てみよう
• nを増やして「置換」のサイクルを見ていこう
• コラム②10種香は何通りか（2）

3章　スターリングのスターリング数

• 「二項係数」の関係式を代数の側面から見てみよう
• 二項係数の「一般項」を場合の数から求めよう
• 「べき乗」を「下降階乗」で表そう
• 「べき乗」を「上昇階乗」で表そう
• 第2種スターリング数の三角形で「列」に着目しよう
• 何を展開すると第２種スターリング数が現れるか
• 第2種スターリング数の「一般項」はどうなるか
• 場合の数の「包除原理」から一般項を求めよう
• 「n!」を「二項係数」で表そう
• 第1種スターリング数の三角形で「列」に着目しよう
• 「第1種スターリング数の多項式」を因数分解しよう
• 「上昇階乗」を「べき乗」で表そう
• 「下降階乗」を「べき乗」で表そう
• 「べき乗」→「下降（上昇）階乗」→「べき乗」
• コラム③攪乱順列とモンモール数

4章　ベル数と無限級数

• 無限和を，ベルヌーイ数を用いて表そう
• 無限和を，ベル数を用いて表そう（1）
• ベル数の「母関数」を求めよう
• 無限和を，ベル数を用いて表そう（2）
• e^xから始め，xをかけて微分していくと…
• xをかけ，それを微分した式とたし算すると…
• 無限級数から第2種スターリング数の「一般項」を…
• 第2種スターリング数の「母関数」を求めよう
• 第1種スターリング数の「母関数」を求めよう
• コラム④ベルヌーイ数と「べき乗和の公式」

5章　スターリングにとっては同一種

• 「パスカルの三角形」をさかのぼろう（1）
• 「マイナス行」を「二項係数」で表そう
• 「マイナス行」に現れた「重複組合せ」とは…
• (1＋x)^－nの展開に着目しよう（1）
• 「パスカルの三角形」をさかのぼろう（2）
• (1＋x)^－nの展開に着目しよう（2）
• 「第2種スターリング数の三角形」をさかのぼろう
• 「マイナス行」に現れた「第1種スターリング数」
• 「逆数のべき乗」を表そう（1）
• 「逆数のべき乗」を表そう（2）
• 「第1種スターリング数の三角形」をさかのぼろう
• 「マイナス行」に現れた「第2種スターリング数」
• 「逆数のべき乗」を用いて表そう
• コラム⑤スターリング数の性質

6章　不思議な「クラウゼン−フォンシュタウトの定理」

• 「上昇階乗」を用いる「積和の公式」とは…
• 「べき乗和」を「スターリング数」で表そう
• 「ベルヌーイ数」を「第2種スターリング数」で表そう
• 「クラウゼン−フォンシュタウトの定理」を見ていこう
• 「第2種スターリング数」を素数pで割った「余り」
• 偶数番目のベルヌーイ数B_2nの「分母」を見てみよう
• 「整数－1/素数－1/素数－…－1/素数」の「整数」を求めよう
• 「ベルヌーイ数」と「スターリング数」が絡んだ式

• 索引
• 参考文献
• 著者プロフィール

サポート

現在サポート情報はありません。