機械学習のカリブレーションとビジネスの関係〜ローンのパーソナライゼーション

本稿は「本当は書籍『評価指標入門』に書きたかったんだけど諸般の理由により書ききれなかった内容をgihyo.jpを借りて成仏させていく企画」の第一段「カリブレーション（Calibration、確率較正⁠）⁠」です。特に「機械学習のカリブレーションとビジネスの関係性を検討」してみたいというモチベーションで執筆します。

日本語では“⁠確率較正⁠”とも呼ばれるこの計算ですが、個人的にはカリブレーションという方が好きなので、ここではカリブレーションと統一して書きます。

早速ですが、まずカリブレーションとは「分類問題において、機械学習モデルの出力（[0, 1]の値）をデータのクラス分布に近づける」ことです。例えば、二値分類問題において、モデルがあるデータ点に対して1を予測する確率が0.8である場合、そのデータ点が実際に1である割合も0.8になるように確率の数値を修正してしまう（これが較正）ということです。事象Aが実際に起こる確率P(A)が0.3なのであれば、事象Aに対する機械学習モデルが出す確率Q(A)も0.3になるようにQを較正するということです。小難しく言うと、QをPの推定量だとみなした時に、Qに対して不偏性を要求するって感じですね。

“確率の値を直に扱う”場合にカリブレーションが必要

まず明らかにしなければならないのは「カリブレーションはそもそもどういう状況の場合考慮しなければならないのか？」です。その答えは“⁠確率の値を直に扱う場合に考慮しなければならない⁠”と言えます。逆に言うと“⁠確率を直に扱わない場合⁠”には考慮する必要はありません。

例えば書籍『評価指標入門』で言うと3章で扱っているEmployee Promotion Dataの場合がこれに相当します。これらの例では確率の値そのものではなく“⁠確率間の大小関係⁠”だけが問題になっているためカリブレーションの必要はありません。例えば、事象AとBがあり、カリブレーション前にはP(A) = 10%, P(B) = 20%であった確率が、カリブレーションによりP(A) = 17%, P(B) = 23%と較正されたとしてもP(A) < P(B)という大小関係が変わらないので、結果は変わらないということです。データサイエンスの文脈では、直感的にはROC-AUCなど“⁠確率間の大小関係⁠”のみで評価可能なケースを扱っている場合には不要、ということです。

既に書籍『評価指標入門』を既にご覧いただいた読者の方は「それって付録に載っているSaaSビジネスの例もそうなのではないか？」とお考えになるかもしれませんが、それは誤りです。付録では確率の値そのものと月額プラン料金Uを掛け算し、その値に基づいて離反防止活動の優先順位を決めているため、大小関係ではなく、確率の値自体が必要であり、したがってカリブレーションの必要性があります。

例「ローン金利のパーソナライゼーション」

ここでは“⁠確率を直に扱う⁠”例、つまりカリブレーションが必要な例として、金融業界では信用リスク管理としてもう十分に研究されて尽くされている領域ではありますが、“⁠ローン金利のパーソナライゼーション⁠”を考えましょう。

さて、あるユーザにローンサービスを提供した結果から得られる利益(Profit)は

\begin{matrix} (A) & Profit = (1 + r) A 1_{{τ > T}} - A \end{matrix}

です。ここでAはユーザへの貸出金額、rは貸出金額Aに対する支払い利息の金利、Tは返済時点, τは“⁠債務不履行になる時刻⁠”（確率変数、この実現値がT（実数）より小さければ債務不履行とみなす）です。A円を現時点tで貸付、将来時点Tで利息を上乗せした(1+r)A円の返済を行っていただく、そしてその差分が利益となるのでもし債務不履行とならなければ(1+r)A - A = rA円が利益となる、というビジネスモデルです。

ただしここで、

分割返済を考えたかったが、生存時間解析が必要なことに気が付いたのでやめた
現在価値への“⁠割引（金融で言うディスカウントファクター）⁠”は数式がゴチャゴチャして見づらくなるので一旦無視（恒等的に1と置いたと等価）

としています。

ここで、あるユーザが債務不履行になるかならないかは現時点t (< T)ではわからないので、利益自体も確率変数とみなす必要があります。利益の期待値を計算すると

\begin{matrix} (B) & E [Profit] = (1 + r) A (\Pr (τ > T) - \frac{1}{1 + r}) \end{matrix}

となります。ここで

\begin{matrix} (C) & E [1_{{τ > T}}] = \Pr (τ > T) \end{matrix}

という関係を用いて、“⁠債務不履行を起こさず返済してくれる⁠”確率Pr(τ > T)を用いた表現としています。逆に債務不履行確率はPr(τ < T) = 1-Pr(τ > T)と計算されます。この確率Pr()を個人の属性に応じて推定し、その結果に依存して金利rも個々人で異なるよう決定するため、ここでは“⁠ローン金利のパーソナライゼーション⁠”という表現を使いました。

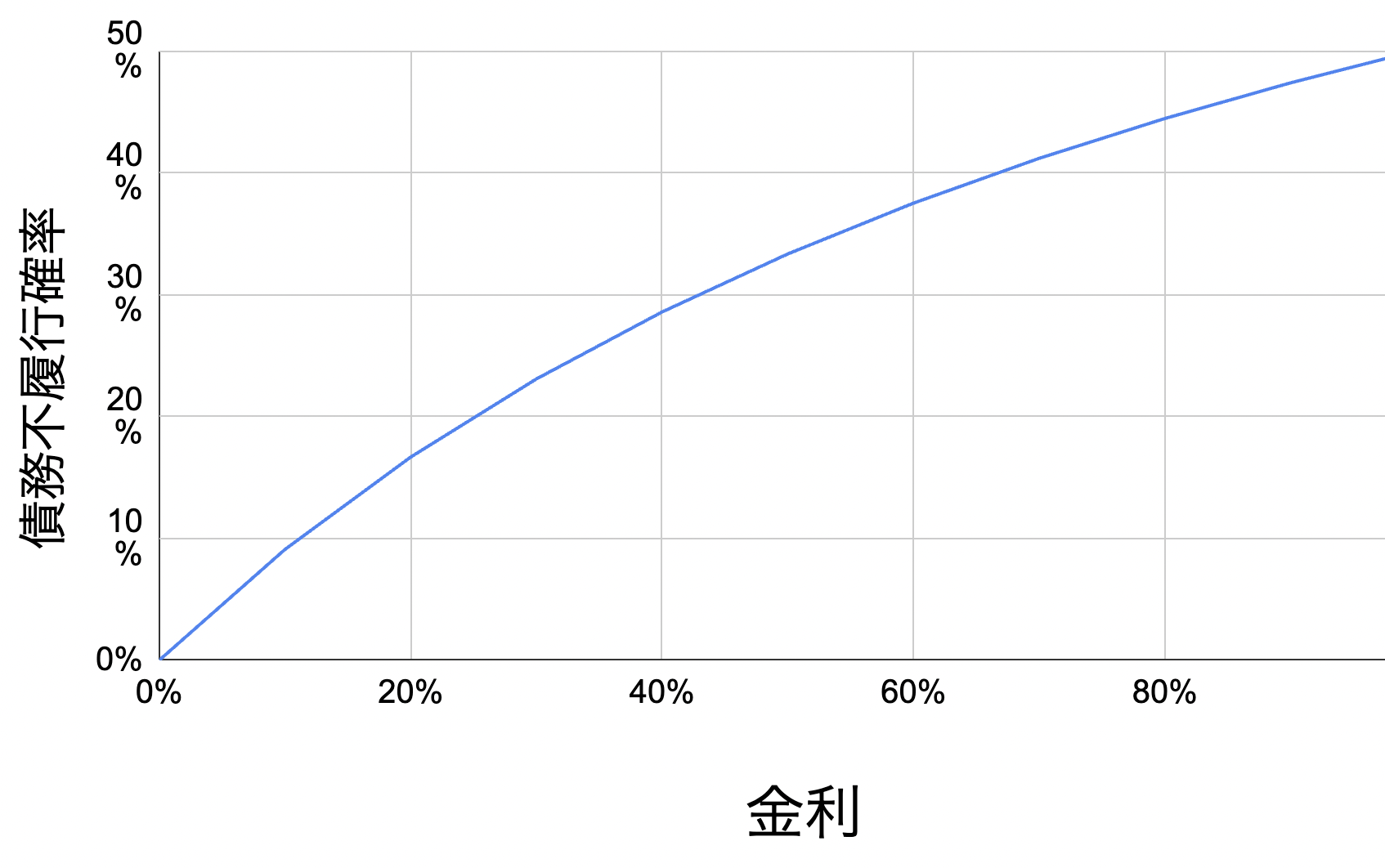
個人的にはこの数式だけでも含蓄が深いもので、一旦ここで可視化をしてみましょう。期待利益が0円になるいわゆる損益分岐点は、数式（B）の括弧の中を0にすることと等価です。このときの金利rと債務不履行確率Pr(τ < T)の関係をグラフにしてみると

となります。日本の法定金利（利息制限法の上限金利）は「年20％」ですので、「⁠金利が20%となる債務不履行確率が17%以上ある場合には貸し付けを見送らざるを得ない」ビジネスということです。実際には、このサービスを提供している会社の資金の調達金利や市場での運用金利、現在価値への割引、などの要因を考慮することになるので多少グラフ形は変わってきますが、ざっくり描くとこんな感じです。

上のグラフを使って、債務不履行確率に応じて金利を決めても良いのですが、それでは期待利益が0円になってしまいこれではビジネスが立ち行きません。なので、ここでは「貸し出し金額Aに対して、債務不履行確率によらず、一定の利益率cを乗せたぶんだけ期待利益として残る」ように金利を設定するとしましょう。利益率cが1%だとすると、100円（A円）貸し出した場合には会社の利益として10円（cA = 1% * 100円）分を利益として上乗せさせていただいた金利で貸し出す、そういうことです。

\begin{matrix} (D) & c A = (1 + r) A \Pr (τ > T) - A \end{matrix}

これを金利rについて解くと

\begin{matrix} (E) & ∴ r = \frac{1 + c}{\Pr (τ > T)} - 1 \end{matrix}

と利益率cを加味した上で金利rを決定することができます。数式のチェックを兼ねて、まず“⁠絶対に債務不履行にならない⁠”⁠、すなわちτをとても大きな数（あるいは∞）としてみましょう。この場合、数式（E）の分母は常に1となるので、結局、

r = c

となります。これは例えば「絶対に債務不履行を起こさないユーザに対して、100円（A）貸した場合、金利（r）を利益率3%（c）に設定して返済していただく状況に対応し「ユーザは103円返済、あなたは3円の利益を得る」といういたってシンプルな状況に対応します。モデルが複雑になればなるほど何を計算しているのか自分でもよくわからなくなるので「ある種の極限（今回の場合は絶対に債務不履行にならない）をとった時に、直感的に自明で常識的な結論に帰着できるか？」を確認することで明らかなミスを犯していないかがわかるためとても重要です。ソフト/ハードウェアエンジニアの方が行うサニティーチェック（sanity check）のようなものと考えると良いでしょう。

以下では「ユーザに対して、特段の区別をしない」とし、利益率cをユーザに依存せず一定の固定値5%だとします。ユーザの債務不履行確率に依存させずに利益率を決めているので、ある意味、平等（equality）であるという状況です。

その他の直感的な考え方として「金利rに一律に下駄（δ）を履かせ、金利をr + δとする」という考え方もありますが、この場合、利益率がユーザに依存し一定とはなりません。興味がある方は数式を変形して本稿の仮定とどういう差が出てくるのかを確認して見ると面白いでしょう（この例をもとに、ワチャワチャ数式をいじっていたときに、著者個人の見解と真逆の結果が出たのが個人的に面白かったポイントです。素人の直感は当てにならないものですね……⁠）⁠。「⁠人間のリスク回避度を加味し、債務不履行確率が高くなるに連れて利益率を高める」というアイディアもあるでしょう。ここはビジネスモデル次第、書籍『評価指標入門』でいうところの「データサイエンスの外側の問題」なので、各社/部署/担当者で決める必要があります。

さて、ここではデータを作るのも面倒なので scikit-learnの make_classification を用いて適当なダミーデータを作ります（設定自体はコードコメントに記載してあります⁠）⁠。

import numpy as np
from collections import defaultdict
import matplotlib.pyplot as plt
from matplotlib.gridspec import GridSpec
import numpy.typing as npt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.calibration import CalibratedClassifierCV, CalibrationDisplay
from sklearn.linear_model import LogisticRegression
from sklearn.naive_bayes import GaussianNB
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import brier_score_loss, log_loss, average_precision_score, roc_auc_score
import pandas as pd

# Train + Testで10万サンプルを生成、標本全体での平均的な債務不履行確率を5%とする
X, y = make_classification(n_samples=100_000, n_features=10, n_informative=7, weights=[0.95, 0.05], random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=43)

#モデルは適当に４つ用意、パラメータは適当
lr = LogisticRegression(C=1.0)
nb = GaussianNB()
rf = RandomForestClassifier(max_depth=3, random_state=71)
nbc = CalibratedClassifierCV(nb, cv=5, method="sigmoid")
clf_list = [(lr, "LR"), (nb, "NB"), (rf, "RF"), (nbc, "NBC")]

作成したデータは1レコードが「ある貸し出しにおいて、債務不履行がある（y=1）かないか（y=0⁠）⁠、残りはyを特徴づける特徴量」という形です。このダミーデータに対して適当な4つのモデル（ロジスティック回帰、ナイーブベイズ、ランダムフォレスト、ナイーブベイズ（カリブレーションあり⁠）⁠）を用意し、債務不履行するかしないかを判定する二値分類問題として解きます。ナイーブベイズにだけカリブレーション（Platt Scaling）を適用していますが他意はなく、ほかのモデルに対して適用してもかまいません。

PythonでのカリブレーションのCodeの書き方や教科書的な評価指標（Brier Score、ECEなど）については

などよく書かれたブログを参考にするのがよく、ここでは説明はしません。

タイトル/冒頭にあるように本稿では「機械学習のカリブレーションとビジネスの関係性」を検討/解説したいのであって「Brier Scoreとは確率の二乗誤差を計算したもので云々」を話したいわけではないからです。

次に「データの示す債務不履行確率と各モデルが予測する債務不履行確率がどの程度一致しているのか？」を示すカリブレーションのプロットを以下のコードで描画します。

fig = plt.figure(figsize=(10, 10))
gs= GridSpec(4, 2)
colors = plt.cm.get_cmap("Dark2")

ax_calibration_curve = fig.add_subplot(gs[:2, :2])
calibration_displays = {}
for i, (clf, name) in enumerate(clf_list):
    clf.fit(X_train, y_train)
    display = CalibrationDisplay.from_estimator(
        clf,
        X_test,
        y_test,
        n_bins=20,
        name=name,
        ax=ax_calibration_curve,
        color=colors(i),
    )
    calibration_displays[name] = display

ax_calibration_curve.set_title("Calibration plots")
plt.show()

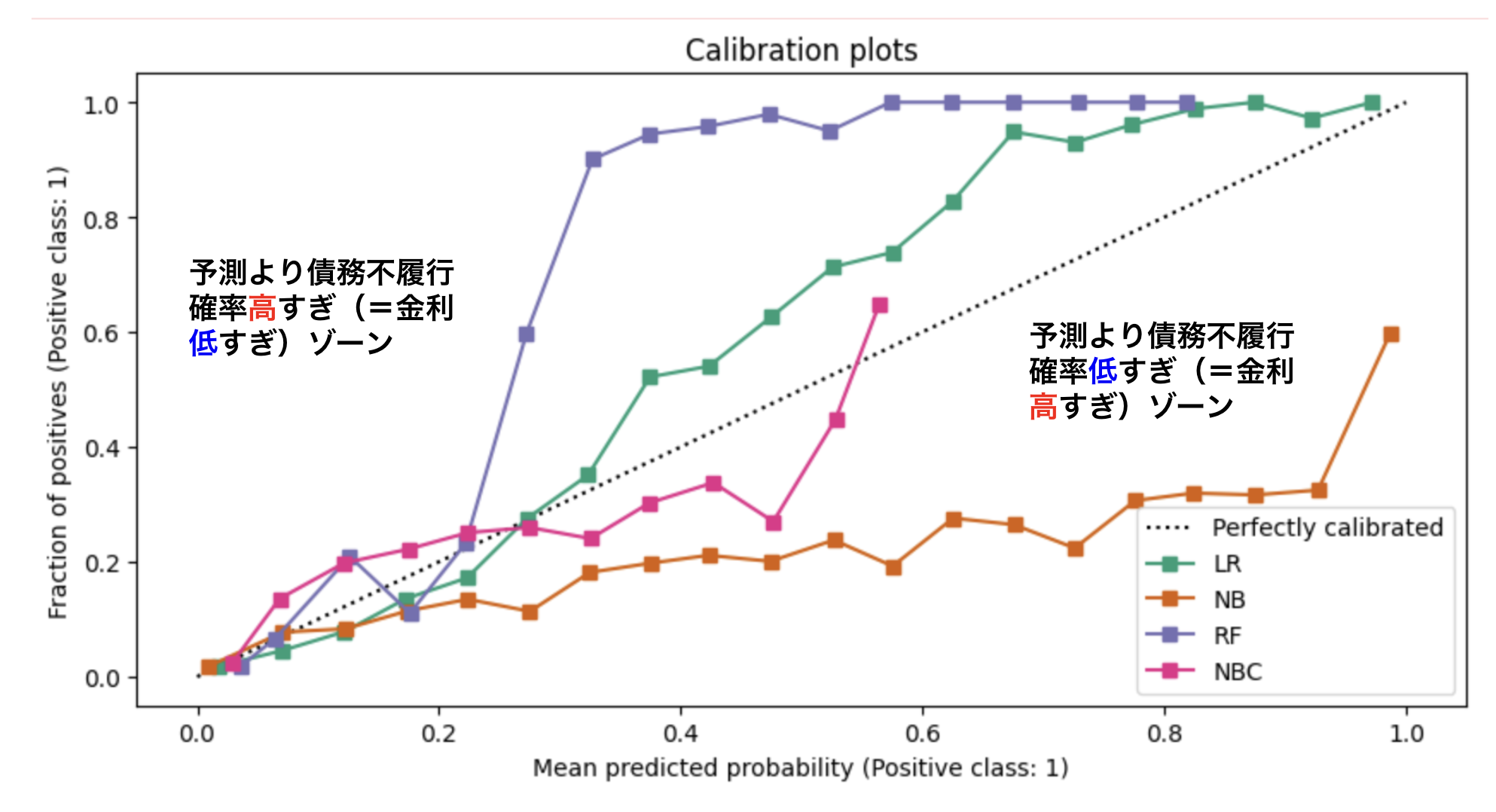
さて、scikit-learnが返してくれるカリブレーション描画結果をビジネス（お金）の視点から解釈していきましょう。図の⁠”Perfectly calibrated⁠”の破線に対して左上の領域は「モデルの予測値より実際の債務不履行確率が高すぎ（＝モデルの出力に応じて設定される金利が低すぎ）て、想定した利益率cを下回り損をしてしまうゾーン（以下、損ゾーン⁠）⁠」に相当します。また、逆に右下の領域は「予測より実際の債務不履行確率が低すぎ（＝モデルの出力に応じて設定される金利が高すぎ）て、儲け過ぎてしまうゾーン（以下、儲ゾーン⁠）⁠」となります。括弧書きした債務不履行確率と確率と金利の関係は数式（E）から読み取れるため、このように解釈することができます。

整理すると

損ゾーンでは債務不履行確率を低めに見積もりすぎるため、利益を圧迫し、場合によっては赤字になってしまう
儲ゾーンでは債務不履行確率を高めに見積もりすぎるため、想定した利益率cよりも多くのユーザから利益を得てしまうことになる

ということになります。それぞれのモデルの線がどちらの領域に入っているのかを見比べることで、債務不履行を過剰／小評価しやすい領域がそれぞれのモデルで異なり特色が出ていると言うこともできます。

例えばナイーブベイズモデル（オレンジ線）だと、機械学習モデルの予測する債務不履行確率が10%を超えたあたりから常に儲ゾーンに入っているので、提示される金利が常に実際にの債務不履行確率に基づいた値よりも割高になっている、ということができます。

なぜカリブレーションが必要なのか？

さて、無事にカリブレーションの計算を終えることができました。次に「そもそもなぜカリブレーションが必要なのか」をこの例においてビジネス（お金）の観点から明らかにしましょう。カリブレーションしなければならない理由はさまざまありますが、以下にその代表例を挙げます。

債務不履行確率を低く見積もってしまう損ゾーンは利益を圧迫する。つまり安売り（低金利貸出）し過ぎているので、ここを減らさないとビジネスとして立ち行かなくなる。ユーザのモラルハザード（自身の債務不履行確率に比べて金利が著しく安い場合、ユーザがお金を借りまくってローンサービスの損失が大きくなる可能性あり）を引き起こす恐れもある
債務不履行確率を高く見積もってしまう儲ゾーンは利益を多くあげることができる。一方、ユーザにとって不利益であり、高すぎる金利の提示はユーザからのサービスへの心象を悪くしLTV（Life Time Value）の低下を招く。また競合他社から見ると、同じ利益率c（5%）を設定しているならば、まだ金利を下げる余地があることを意味し顧客の流出を招き得る
利益率cが指定した値（ここでは5%）になるのは、機械学習モデルの吐き出す債務不履行確率が完全にカリブレーションされている場合である。例えばナイーブベイズモデルの場合、カリブレーションは明らかになされていないのでユーザごとの利益率がバラつく

最初の1と2は簡潔に言うと1：「安売り（金利低）すぎて利益が出ない」2：「高値（高金利）でサービスを売ろうとして、（⁠ユーザが「ここの金利高いな…使わないでおこう」と思うなどし）ユーザ離反を招く、使う人数が減ってしまう」ということです。

3を解釈するにはもう少しビジネス的な視点が必要です。ここではユーザによらず利益率cが一定であると仮定していたのでした。こうすることで得られるメリットは、「⁠貸出金額Ax 利益率c」を計算することで「現状の貸出の返済時点Tにおいてどのくらい利益があがるのか」が大まかに把握できるということです。これは経営上とても強いアドバンテージとなりえます。

例えば

貸出金額と利益率から、現時点での利益の着地点が見えるので、目標との乖離を計算しそこを埋めるための施策を考えることができる
- 例：あえて金利を下げて薄利多売にしてでも貸出額を増やす
- 例：マーケティング施策を行い新規顧客を増やす
各月単位などでの将来時点での利益（手元に入ってくる現金）が見えるので資金繰りの計画が立てやすい

を考えることができるでしょう。書籍『評価指標入門』では「利益を最大化」するケースをいくつか扱っているのですが、今回は上記の理由から、利益の最大化ではなく（これはサービスのアクティブなユーザ数を減らさないよう制約を課しつつ、貸出の金利を最大化する（目標利益率を上げる）ことで達成できます⁠）⁠、「⁠目標としている利益率cに近しい値を達成できるか？」を目標としましょう。つまり「クロスバリデーションした結果、利益率が指定した値c（5%）に最も近かったモデルを良いモデルだとしよう」ということです。

def interest_rate(c: float, prob: npt.ArrayLike) -> npt.ArrayLike:
    """数式にそって金利を計算する関数

    Args:
        c(float): 利益率
        prob(npt.ArrayLike): 債務不履行確率のベクトル

    Returns:
        npt.ArrayLike: 貸出の金利
    """
    # prob == 1 の場合を避けるためのおまじない
    epsilon = 1e-6
    return((1 + c)/(1 - prob + epsilon) - 1)

def profit(A: float, r: npt.ArrayLike, y: npt.ArrayLike):
    """数式にそって利益を計算する関数

    Args:
        A(float): 貸出金額
        r(npt.ArrayLike): 金利のベクトル
        y(npt.ArrayLike): 債務不履行(1) or not(0)のベクトル

    Returns:
        npt.ArrayLike: 利益
    """
    return((1 + r) * A * (1 - y) - A)


# 貸出金額
A = 1
# 利益率
c = 0.05
# 利息制限法の上限金利20％/年
r_upper = 0.2
# A円をlen(y_test)人に利益率cで貸し出した場合の利益（合計）
sum_profit_expected = c * A * len(y_test)

scores = defaultdict(list)
for i, (clf, name) in enumerate(clf_list):
    clf.fit(X_train, y_train)
    y_prob = clf.predict_proba(X_test)
    y_pred = clf.predict(X_test)
    scores["Classifier"].append(name)

    for metric in [brier_score_loss, log_loss]:
        score_name = metric.__name__.replace("_", " ").replace("score", "").capitalize()
        scores[score_name].append(metric(y_test, y_prob[:, 1]))

    for metric in [average_precision_score, roc_auc_score]:
        score_name = metric.__name__.replace("_", " ").replace("score", "").capitalize()
        scores[score_name].append(metric(y_test, y_pred))

    # 金利、利益（ベクトル and 合計）の計算
    r = interest_rate(c, y_prob[:, 1])
    p = profit(A, r, y_test)
    profit_rate = sum(p)/(A*len(y_test))
    # 利息制限法の上限金利20％/年を考慮した版の計算
    profit_rate_limited = sum(p * (r < r_upper))/(A*sum(r < r_upper))
    # スコア化
    scores["Profit Rate"].append(profit_rate)
    scores["Profit Rate (limited)"].append(profit_rate_limited)

    score_df = pd.DataFrame(scores).set_index("Classifier")

pd.options.display.precision = 4
score_df

計算した結果、以下のようになります。

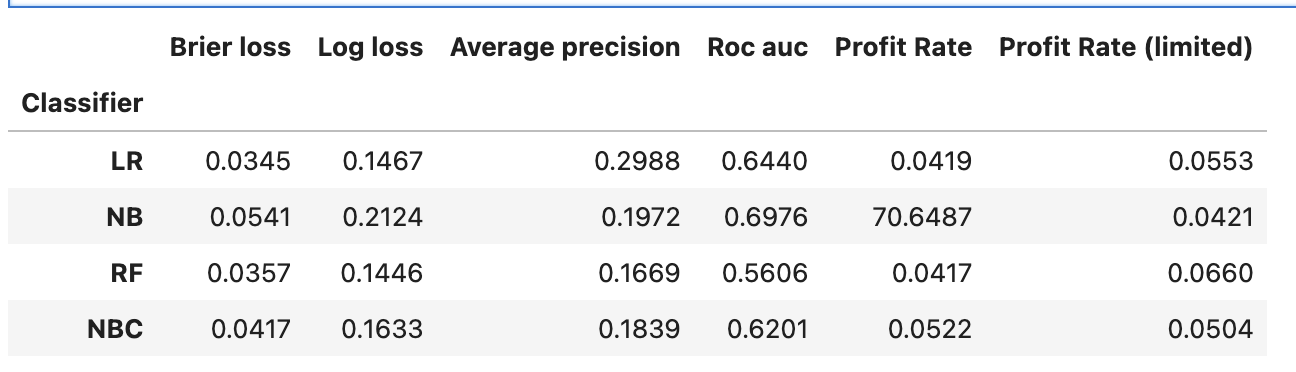
確率を使って評価する評価指標brier lossやlog lossではロジスティック回帰（LR）やランダムフォレスト（RF）が良さそうな一方、AUC（PR、ROC）ではLRやNBも善戦しています。一方、本稿で目標にしようと宣言した利益率（Profit Rate）で見ると、カリブレーションしたナイーブベイズ（NBC）が最も指定した利益率5%に近く、経営の見通しがよくなるという意味で良いモデルである、ということができそうです[1]。

また、日本の法定金利（20%）を考慮した結果をProfit Rate (limited)として記載していますが、こちらでもNBCの調子が一番良さそうです。したがって、この例の場合、AUCや適当なロス関数での評価は「利益率がちゃんと設定した値になっているか？」という意味で適切なものではなかった、ということになります。

このような“⁠評価指標の考え方⁠”について解説した書籍『評価指標入門』を2023年2月に上梓したばかりですので、まだ読んだことがない方はぜひ手に取ってみてください！