1. 時系列分析とは

時系列分析とは時間的に得られる系列的なデータに対する分析のことですが，まずは実際のデータを元にその感触を確かめてみましょう。ここでは，データを二つ取り上げます。

最初に，アフリカ大陸のナイル川における年間流量に関するデータを確認してみます。このデータは1871年から1970年までの年ごとの観測値の系列（単位は[×10⁸m³]）になっています。図1はそのグラフになります。

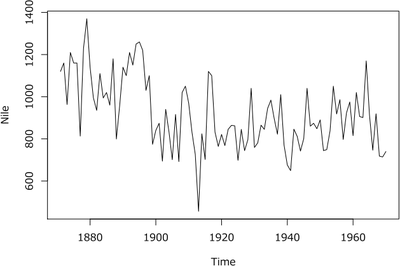
図1を眺めると，その年の気候に左右されるためか不規則な変動が続いており，特別なパタンは見受けられないような印象を受けます。ナイル川の氾濫は流域の安全や農作に大きく影響を及ぼすためエジプト文明の発展とも深い関係があり，近代には氾濫を人工的に制御する目的でアスワンダムが建設されています。ナイル川の流量は毎年変動していますが，過去・現在・未来にわたってどのような値を取り，またどのような傾向があるのかを適切に把握することは，文明の発展に関する考察や安全対策，農作の管理などに有益です。

続いて，大気中の二酸化炭素濃度に関するデータを確認してみましょう。ここでは国内における最新の観測値を取り上げます。具体的には，岩手県大船渡市三陸町綾里崎において1987年1月から観測されている月平均値の系列（単位は[ppm]）を考えます。図2は，このデータの2014年12月までのグラフになります。

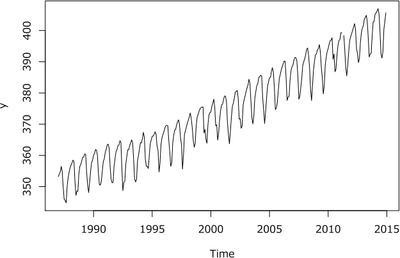
図2をよく見ると，2011年4月に描画が欠けていることがわかります。これは，同時期に発生した東日本大震災の影響で，データが取得できなかった部分です。また図2には，明確な年周期のパタンが見受けられます。これにはさまざまな要因が考えられますが，植物の生態（おおむね冬場より夏場の方が光合成が盛んなど）も影響しています。更に全体的には右肩上がりの傾向があり，このことが地球温暖化の要因の一つとして近年認識されるようになってきました。大気中の二酸化炭素濃度は毎年変動していますが，過去・現在・未来にわたってどのような値を取り，またどのような傾向があるのかを適切に把握することは，植物の生態に関する考察や地球温暖化の対策などに有益な営みとなります。

以上の例を踏まえて時系列分析の一般的な意味合いを改めて考えてみると，基本的には関心のある事象における過去・現在・未来の値を適切に把握し（推定し⁠）⁠，関連してその結果を元に，事象の仕組みや影響に関する知見を得たり対策を考えたりする営みである，といえるでしょう。

時系列分析では，過去と現在，さらに未来それぞれの値を適切に推定することになります。この3種類の推定は図3に示すように，過去の時点に対する推定は平滑化（もしくはスムージング⁠）⁠，現在の時点に対する推定はフィルタリング（もしくは濾波⁠）⁠，未来の時点に対する推定は予測（もしくはプレディクション／フォアキャスト）と呼ばれます。

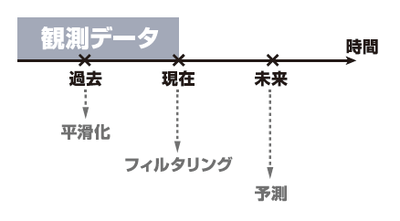
2. 時系列分析のアプローチ

時系列データの分析が素朴な統計分析と最も異なるのは，各時点のデータの間の関連を明確に考慮する点にあります。

一般に時系列データはサイコロの出目などとは異なり，各時点のデータの間で何らかの関係をもっています。

例えば前節でのナイル川における年間流量のデータでいえば，特別なパタンがないということは，不規則なふらつきを除けば毎年おおむね前年と似た値を繰り返しているのではないか，という推察ができます。また，前節での大気中の二酸化炭素濃度データに関しては，年周期のパタンと右肩上がりの傾向があるのではないか，という推察ができます。

このようにデータのもつ時間方向の相関は，推定精度を向上させるために考慮すべき有意義な情報です。本稿ではこのために，柔軟性の高い確率的なモデルの一種である状態空間モデル（State Space Model）に基づく方法を説明します。

3. 状態空間モデルによる推定の例

状態空間モデルでは，直接は観測できない潜在的な「状態」という変数を想定し，得られた観測値を元に，この「状態」が従う確率分布を推定します。状態空間モデルにおける状態の推定にはいろいろな方法がありますが，基本的にはベイズの定理に基づくベイズ更新「事後分布は事前分布×尤度（ゆうど）に比例する」が元になっています（尤度とは，想定した確率分布に観測値がどれくらい当てはまっているのかを示す度合のことです⁠）⁠。ここではそのイメージをつかんでもらうために，簡単なフィルタリングの例を紹介します。

それでは，具体的な説明に移りましょう。人工的な問題ではありますが，図4のように飼いネコの行動を確認するために，首輪にGPS発信器を付けて観測するような状況を考えます。

実際のネコの行動は気まぐれでモデル化は容易ではないと思われますが，ここでは簡単に飼い家から平均速度νで直線的に離れていくような場合を想定します。

そしてこの問題が，次のような線形・ガウス型と呼ばれる状態空間モデルで定義されるとします（$\mathcal{N}(\mu, \sigma^2)$は，平均$\mu$, 分散$\sigma^2$の正規分布を意味しています⁠）⁠。

$$ \begin{align} x_t &= x_{t-1}+\nu+w_t & w_t &\sim \mathcal{N}(0, \sigma^2_w) \tag{1} \\ y_t &= x_t+v_t & v_t &\sim \mathcal{N}(0, \sigma^2) \tag{2} \end{align} $$

ここで観測開始時の$t=1$より前に，事前の知見に基づき$t=1$の位置を推測した値を$m_{0}=\hat{m}_{1}$とし，その確信度合を分散$C_{0}$で表すことにします。(1), (2)式において，$x_{t}$は時点$t$におけるネコの位置，$\nu$は平均速度（定数⁠）⁠，$w_{t}$は移動時の速度の揺らぎ，$y_{t}$は時点tにおける観測値，$\nu_{t}$は観測時の雑音となります。

状態を逐次的に求める過程を確認してみます。それが図5になります。この図では時間の進展が下方向，ネコの移動が右方向で表されています。

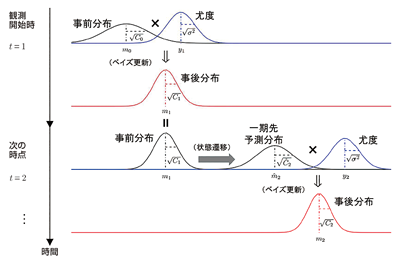
まず観測開始時の$t=1$では，ネコが動き始める時にどの位置にいたかを推定します。最初に事前情報に基づき事前分布が存在していますので，この事前分布に$t=1$で得られた観測値に基づく尤度をかけると，$t=1$における事後分布が得られます（ベイズ更新⁠）⁠。尤度を考慮することで確からしさが増しますので，事後分布の分散は事前分布の分散より小さくなっています。この事後分布が，ネコが観測開始時にどの位置にいたかを推定した結果になります。

続いて時点$t=2$では，ネコが動き始めてから次の時点でどの位置にいたかを推定します。$t=2$における事前分布は$t=1$における事後分布に相当しています。今度はネコが動いている状況ですので，この事前分布に対して平均速度を踏まえた移動が最初に考慮されます（これを状態遷移といいます⁠）⁠。ただし移動速度にも揺らぎ$w_{t}$があるため移動に伴い不確かさが増え，移動後を予測する一期先予測分布では分散が事前分布に比べ増えてしまいますが，これはしかたありません。 この移動後を予測した一期先予測分布に，$t=2$で得られた観測値に基づく尤度をかけると，$t=2$における事後分布が得られます（ベイズ更新⁠）⁠。

尤度を考慮することで確からしさが増しますので，事後分布の分散は移動後を予測した分布より分散が小さくなります。この事後分布が，ネコが次の時点でどの位置にいたかを推定した結果になります。

このようにして，状態遷移とベイズ更新を繰り返すことで推定する分布を更新していきます。具体的な式の変化は割愛しますが，この結果は実はカルマンフィルタと呼ばれる処理の簡単な例になっています。

4. おわりに

本稿では時系列データの分析（時系列分析）とはどのようなものかを紹介し，状態空間モデルに基づく簡単な例を説明しました。時系列分析にはさらに奥深い世界が広がっており，最近では検討をサポートする計算機ソフトウェア環境（R言語など）も拡充されていますので，皆さんもチャレンジしてみてはいかがでしょうか。