前回の第15回
z座標を加えてy軸で回す
前回述べた通り、
{x:x座標値, y:y座標値, z:z座標値}第15回コード3に新たな関数
function createStarPoints(numVertices, longRadius, shortRadius) {
var starPoints = [];
var angle = Math.PI;
var theta = angle / numVertices;
angle /= -2;
for (var i = 0; i < numVertices; i++) {
// starPoints.push(new createjs.Point(longRadius * Math.cos(angle), longRadius * Math.sin(angle)));
starPoints.push(newPoint3D(longRadius * Math.cos(angle), longRadius * Math.sin(angle), 0));
angle += theta;
// starPoints.push(new createjs.Point(shortRadius * Math.cos(angle), shortRadius * Math.sin(angle)));
starPoints.push(newPoint3D(shortRadius * Math.cos(angle), shortRadius * Math.sin(angle), 0));
angle += theta;
}
return starPoints;
}
function newPoint3D(x, y, z) {
var point3D = {x:x, y:y, z:z};
return point3D;
}この書替えをしても、


では、

だったら、
var _point = new createjs.Point();
function rotate(eventObject) {
var count = points.length;
matrix.identity().rotate(angle);
for (var i = 0; i < count; i++) {
var point = points[i];
// matrix.transformPoint(point.x, point.y, point);
matrix.transformPoint(point.x, point.z, _point);
point.x = _point.x;
point.z = _point.y;
}
draw(points);
}これで、


var stage;
var drawGraphics;
var points;
var angle = Math.PI / 36;
var matrix = new createjs.Matrix2D();
var stageCenterX;
var _point = new createjs.Point();
function initialize() {
var canvasElement = document.getElementById("myCanvas");
stage = new createjs.Stage(canvasElement);
stageCenterX = canvasElement.width / 2;
drawGraphics = createGraphics(stageCenterX, canvasElement.height / 2);
points = createStarPoints(5, 65, 25);
draw(points);
createjs.Ticker.addEventListener("tick", rotate);
stage.addEventListener("stagemousemove", setAngle);
}
function setAngle(eventObject) {
var mouseX = eventObject.stageX;
angle = (mouseX - stageCenterX) * 1 / 300;
}
function rotate(eventObject) {
var count = points.length;
matrix.identity().rotate(angle);
for (var i = 0; i < count; i++) {
var point = points[i];
matrix.transformPoint(point.x, point.z, _point);
point.x = _point.x;
point.z = _point.y;
}
draw(points);
}
function createGraphics(x, y) {
var drawShape = new createjs.Shape();
drawShape.x = x;
drawShape.y = y;
stage.addChild(drawShape);
return drawShape.graphics;
}
function draw(points) {
var count = points.length;
var point = points[count - 1];
drawGraphics.clear()
.beginStroke("mediumblue")
.setStrokeStyle(3)
.moveTo(point.x, point.y);
for (var i = 0; i < count; i++) {
point = points[i];
drawGraphics.lineTo(point.x, point.y);
}
stage.update();
}
function createStarPoints(numVertices, longRadius, shortRadius) {
var starPoints = [];
var angle = Math.PI;
var theta = angle / numVertices;
angle /= -2;
for (var i = 0; i < numVertices; i++) {
starPoints.push(newPoint3D(longRadius * Math.cos(angle), longRadius * Math.sin(angle), 0));
angle += theta;
starPoints.push(newPoint3D(shortRadius * Math.cos(angle), shortRadius * Math.sin(angle), 0));
angle += theta;
}
return starPoints;
}
function newPoint3D(x, y, z) {
var point3D = {x:x, y:y, z:z};
return point3D;
}遠近法の投影(透視投影)
コンピュータグラフィックス
遠近法では、
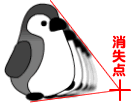
また、
ふたつのものの奥行きの距離は、
焦点距離は、
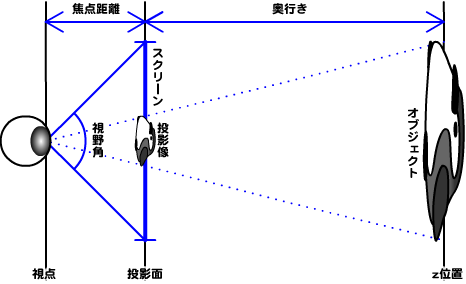
実際のオブジェクトと投影像をそれぞれ底辺とし、
投影像の大きさ/オブジェクトの大きさ = 焦点距離 / (焦点距離 + z位置)
投影像の大きさ = オブジェクトの大きさ×焦点距離 / (焦点距離 + z位置)したがって、
透視投影比率 = 焦点距離 / (焦点距離 + z位置)3次元空間座標を透視投影する
前掲コード1に、
焦点距離は変数
透視投影の関数
var points2D = [];
var focalLength = 300;
function rotate(eventObject) {
var count = points.length;
points2D.length = 0;
matrix.identity().rotate(angle);
for (var i = 0; i < count; i++) {
var point = points[i];
matrix.transformPoint(point.x, point.z, _point);
point.x = _point.x;
point.z = _point.y;
points2D[i] = getProjetedPoint(focalLength, point);
}
// draw(points);
draw(points2D);
}
function getProjetedPoint(focalLength, _point3D) {
var point2D = new createjs.Point();
var w = focalLength / (focalLength + _point3D.z);
point2D.x = _point3D.x * w;
point2D.y = _point3D.y * w;
return point2D;
}なお、
前掲コード1にこれらの遠近法の計算を加えたのが、


var stage;
var drawGraphics;
var points;
var angle = Math.PI / 36;
var matrix = new createjs.Matrix2D();
var stageCenterX;
var _point = new createjs.Point();
var points2D = [];
var focalLength = 300;
function initialize() {
var canvasElement = document.getElementById("myCanvas");
stage = new createjs.Stage(canvasElement);
stageCenterX = canvasElement.width / 2;
drawGraphics = createGraphics(stageCenterX, canvasElement.height / 2);
points = createStarPoints(5, 65, 25);
draw(points);
createjs.Ticker.addEventListener("tick", rotate);
stage.addEventListener("stagemousemove", setAngle);
}
function setAngle(eventObject) {
var mouseX = eventObject.stageX;
angle = (mouseX - stageCenterX) * 1 / 300;
}
function rotate(eventObject) {
var count = points.length;
points2D.length = 0;
matrix.identity().rotate(angle);
for (var i = 0; i < count; i++) {
var point = points[i];
matrix.transformPoint(point.x, point.z, _point);
point.x = _point.x;
point.z = _point.y;
points2D[i] = getProjetedPoint(focalLength, point);
}
draw(points2D);
}
function createGraphics(x, y) {
var drawShape = new createjs.Shape();
drawShape.x = x;
drawShape.y = y;
stage.addChild(drawShape);
return drawShape.graphics;
}
function draw(points) {
var count = points.length;
var point = points[count - 1];
drawGraphics.clear()
.beginStroke("mediumblue")
.setStrokeStyle(3)
.moveTo(point.x, point.y);
for (var i = 0; i < count; i++) {
point = points[i];
drawGraphics.lineTo(point.x, point.y);
}
stage.update();
}
function createStarPoints(numVertices, longRadius, shortRadius) {
var starPoints = [];
var angle = Math.PI;
var theta = angle / numVertices;
angle /= -2;
for (var i = 0; i < numVertices; i++) {
starPoints.push(newPoint3D(longRadius * Math.cos(angle), longRadius * Math.sin(angle), 0));
angle += theta;
starPoints.push(newPoint3D(shortRadius * Math.cos(angle), shortRadius * Math.sin(angle), 0));
angle += theta;
}
return starPoints;
}
function getProjetedPoint(focalLength, _point3D) {
var point2D = new createjs.Point();
var w = focalLength / (focalLength + _point3D.z);
point2D.x = _point3D.x * w;
point2D.y = _point3D.y * w;
return point2D;
}
function newPoint3D(x, y, z) {
var point3D = {x:x, y:y, z:z};
return point3D;
}前掲コード2で焦点距離
コード2の値
今回のお題の表現は、







