今回から取り組むお題は，
楕円軌道を描いて動かす
今回のスクリプトは以下のような組立てにしよう。楕円軌道で動くパーティクルは，
<script src="http://code.createjs.com/easeljs-0.7.1.min.js"></script>
<script>
function Particle(設定の引数) {
// パーティクルの生成
}
Particle.prototype = new createjs.Shape();
</script>
<script>
var stage;
var particle;
function initialize() {
var canvasElement = document.getElementById("myCanvas");
stage = new createjs.Stage(canvasElement);
particle = new Particle(設定の引数);
// 初期化の処理
}
</script>
<body onLoad="initialize()">
<canvas id="myCanvas" width="240" height="180"></canvas>
</body>
さて，
- 水平座標(x) = 水平中心座標 + 半径×cos角度
- 垂直座標(y) = 垂直中心座標 + 半径×sin角度
第11回 図4 原点から距離が1で角度θのxy座標は
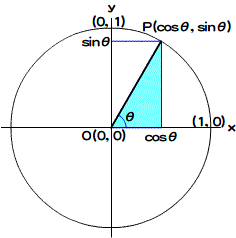
円軌道を楕円にするには，
Particle.prototype.move = function(advance) {
var angle = this.angle + advance;
this.x = this.centerX + this.radius * Math.cos(angle);
this.y = this.centerY + this.radius * 0.8 * Math.sin(angle);
this.angle = angle;
};
パーティクルを定めるクラス
コード1 パーティクルを定めるクラス
function Particle(radius, color) {
this.initialize();
this.graphics.beginFill(color)
.drawCircle(0, 0, radius)
.endFill();
this.compositeOperation = "lighter";
}
Particle.prototype = new createjs.Shape();
Particle.prototype.reset = function(x, y, radius, angle) {
this.centerX = x;
this.centerY = y;
this.radius = radius;
this.angle = angle;
};
Particle.prototype.move = function(advance) {
var angle = this.angle + advance;
this.x = this.centerX + this.radius * Math.cos (angle);
this.y = this.centerY + this.radius * 0.8 * Math.sin (angle);
this.angle = angle;
};
パーティクルのインスタンス
また，
図1 丸いパーティクルが楕円軌道を描いて回る
コード2 クラスでつくったオブジェクトひとつを楕円軌道で回す
var stage;
var center = new createjs.Point();
var particle;
function initialize() {
var canvasElement = document.getElementById("myCanvas");
var stageWidth = canvasElement.width;
var stageHeight = canvasElement.height;
stage = new createjs.Stage(canvasElement);
center.x = stageWidth / 2;
center.y = stageHeight / 2;
particle = new Particle(4, "#0016E9");
resetParticle(particle);
stage.addChild(particle);
createjs.Ticker.timingMode = createjs.Ticker.RAF;
createjs.Ticker.addEventListener("tick", tick);
}
function resetParticle(particle) {
var radius = 40 + Math.random() * 50;
var angle = Math.random() * Math.PI * 2;
particle.reset(center.x, center.y, radius, angle);
}
function tick() {
moveParticle(particle);
stage.update();
}
function moveParticle(particle) {
particle.move(Math.PI / 90);
}
