前回の第31回
点と棒で組上げた三角形を落とす
前回、
function VerletPoint(x, y) {
this.x = this._oldX = x;
this.y = this._oldY = y;
}
VerletPoint.prototype.update = function() {
var tempX = this.x;
var tempY = this.y;
var velocity = this.getVelocity();
this.addCoordinates(velocity.x, velocity.y);
this._oldX = tempX;
this._oldY = tempY;
};
VerletPoint.prototype.constrain = function(rect) {
var left = rect.x;
var right = left + rect.width;
var top = rect.y;
var bottom = top + rect.height;
if (this.x < left) {
this.x = left;
} else if (this.x > right) {
this.x = right;
}
if (this.y < top) {
this.y = top;
} else if (this.y > bottom) {
this.y = bottom;
}
};
VerletPoint.prototype.getVelocity = function() {
var velocity = new createjs.Point(this.x - this._oldX, this.y - this._oldY);
return velocity;
};
VerletPoint.prototype.render = function(graphics) {
graphics.beginFill("black")
.drawCircle(this.x, this.y, 2.5)
.endFill();
};
VerletPoint.prototype.addCoordinates = function(x, y) {
this.x += x;
this.y += y;
};
VerletPoint.prototype.subtract = function(_point) {
var subtractedPoint = new VerletPoint(this.x - _point.x, this.y - _point.y);
return subtractedPoint;
};
VerletPoint.prototype.getLength = function() {
var dx = this.x;
var dy = this.y;
var length = Math.sqrt(dx * dx + dy * dy);
return length;
};
VerletPoint.prototype.getDistance = function(_point) {
var distancePoint = this.subtract(_point);
return distancePoint.getLength();
};function VerletStick(point0, point1, length, elasticity) {
if (!elasticity || elasticity > 0.5 || 0 > elasticity) {
this.elasticity = 0.2;
} else {
this.elasticity = elasticity;
}
this._point0 = point0;
this._point1 = point1;
if (!length || length < 0) {
this._length = point0.getDistance(point1);
} else {
this._length = length;
}
}
VerletStick.prototype.update = function() {
var delta = this._point1.subtract(this._point0);
var distance = delta.getLength();
var difference = this._length - distance;
var offsetX = (difference * delta.x / distance) * this.elasticity;
var offsetY = (difference * delta.y / distance) * this.elasticity;
this._point0.addCoordinates(-offsetX, -offsetY);
this._point1.addCoordinates(offsetX, offsetY);
};
VerletStick.prototype.render = function(graphics) {
graphics.beginStroke("black")
.setStrokeStyle(0.5)
.moveTo(this._point0.x, this._point0.y)
.lineTo(this._point1.x, this._point1.y);
};そして、
そして、
makePoints(中心x座標, 中心y座標, 半径, 頂点数)多角形の頂点をつくるこの関数は、
// var _stick;
var _sticks = [];
var _radius = 50;
function initialize() {
// _points.push(new VerletPoint(70, 100));
// _points.push(new VerletPoint(50, 25));
makePoints(100, 70, 50, 3);
// _stick = new VerletStick(_points[0], _points[1]);
makeSticks();
}
function makePoints(centerX, centerY, radius, vertices) {
var angle = -Math.PI / 2;
var theta = 2 * Math.PI / vertices;
for (var i = 0; i < vertices; i++) {
var x = centerX + radius * Math.cos(angle);
var y = centerY + radius * Math.sin(angle);
_points.push(new VerletPoint(x, y));
angle += theta;
}
}
function makeSticks() {
var count = _points.length;
for (var i = 0; i < count - 1; i++) {
_sticks.push(new VerletStick(_points[i], _points[i + 1]));
}
_sticks.push(new VerletStick(_points[i], _points[0]));
}Ticker.
function draw(eventObject) {
// _stick.update();
updateSticks();
// _stick.render(drawingGraphics);
renderSticks();
}
function updateSticks() {
var count = _sticks.length;
for (var i = 0; i < count; i++) {
var stick = _sticks[i];
stick.update();
}
}
function renderSticks() {
var count = _sticks.length;
for (var i = 0; i < count; i++) {
var stick = _sticks[i];
stick.render(drawingGraphics);
}
}これらの書き替えを終えたJavaScriptが以下のコード1だ。3つの点と棒で三角形をつくって、
var stage;
var drawingGraphics;
var _points = [];
var _sticks = [];
var _stageRect;
var velocityX = 5;
var velocityY = 0.25;
var _radius = 50;
function initialize() {
var canvasElement = document.getElementById("myCanvas");
var shape = new createjs.Shape();
stage = new createjs.Stage(canvasElement);
stage.addChild(shape);
drawingGraphics = shape.graphics;
_stageRect = new createjs.Rectangle(
_radius / 8,
_radius / 8,
canvasElement.width - _radius / 4,
canvasElement.height - _radius / 4
);
makePoints(100, 70, 50, 3);
makeSticks();
_points[0].x += velocityX;
createjs.Ticker.timingMode = createjs.Ticker.RAF;
createjs.Ticker.addEventListener("tick", draw);
}
function draw(eventObject) {
updatePoints();
updateSticks();
drawingGraphics.clear();
renderPoints();
renderSticks();
stage.update();
}
function makePoints(centerX, centerY, radius, vertices) {
var angle = -Math.PI / 2;
var theta = 2 * Math.PI / vertices;
for (var i = 0; i < vertices; i++) {
var x = centerX + radius * Math.cos(angle);
var y = centerY + radius * Math.sin(angle);
_points.push(new VerletPoint(x, y));
angle += theta;
}
}
function makeSticks() {
var count = _points.length;
for (var i = 0; i < count - 1; i++) {
_sticks.push(new VerletStick(_points[i], _points[i + 1]));
}
_sticks.push(new VerletStick(_points[i], _points[0]));
}
function updatePoints() {
var count = _points.length;
for (var i = 0; i < count; i++) {
var point = _points[i];
point.y += velocityY;
point.update();
point.constrain(_stageRect);
}
}
function updateSticks() {
var count = _sticks.length;
for (var i = 0; i < count; i++) {
var stick = _sticks[i];
stick.update();
}
}
function renderPoints() {
var count = _points.length;
for (var i = 0; i < count; i++) {
var point = _points[i];
point.render(drawingGraphics);
}
}
function renderSticks() {
var count = _sticks.length;
for (var i = 0; i < count; i++) {
var stick = _sticks[i];
stick.render(drawingGraphics);
}
}4つの点から四角形をつくって落とす
三角形ができたら、
function initialize() {
makePoints(100, 70, 50, 4); // 3);
}
問題は、
function makeSticks() {
var count = _points.length;
for (var i = 0; i < count - 1; i++) {
_sticks.push(new VerletStick(_points[i], _points[i + 1]));
}
_sticks.push(new VerletStick(_points[i], _points[0]));
_sticks.push(new VerletStick(_points[0], _points[2])); // 追加
}しかし、
function makeSticks() {
var count = _points.length;
for (var i = 0; i < count - 1; i++) {
// _sticks.push(new VerletStick(_points[i], _points[i + 1]));
for (var j = i + 1; j < count; j++) {
_sticks.push(new VerletStick(_points[i], _points[j], null, 0.1));
}
}
// _sticks.push(new VerletStick(_points[i], _points[0]));
}この修正を前掲コード1に加えたのが、
var stage;
var drawingGraphics;
var _points = [];
var _sticks = [];
var _stageRect;
var velocityX = 5;
var velocityY = 0.25;
var _radius = 50;
function initialize() {
var canvasElement = document.getElementById("myCanvas");
var shape = new createjs.Shape();
stage = new createjs.Stage(canvasElement);
stage.addChild(shape);
drawingGraphics = shape.graphics;
_stageRect = new createjs.Rectangle(
_radius / 8,
_radius / 8,
canvasElement.width - _radius / 4,
canvasElement.height - _radius / 4
);
makePoints(100, 70, 50, 4);
makeSticks();
_points[0].x += velocityX;
createjs.Ticker.timingMode = createjs.Ticker.RAF;
createjs.Ticker.addEventListener("tick", draw);
}
function draw(eventObject) {
updatePoints();
updateSticks();
drawingGraphics.clear();
renderPoints();
renderSticks();
stage.update();
}
function makePoints(centerX, centerY, radius, vertices) {
var angle = -Math.PI / 2;
var theta = 2 * Math.PI / vertices;
for (var i = 0; i < vertices; i++) {
var x = centerX + radius * Math.cos(angle);
var y = centerY + radius * Math.sin(angle);
_points.push(new VerletPoint(x, y));
angle += theta;
}
}
function makeSticks() {
var count = _points.length;
for (var i = 0; i < count - 1; i++) {
for (var j = i + 1; j < count; j++) {
_sticks.push(new VerletStick(_points[i], _points[j]));
}
}
}
function updatePoints() {
var count = _points.length;
for (var i = 0; i < count; i++) {
var point = _points[i];
point.y += velocityY;
point.update();
point.constrain(_stageRect);
}
}
function updateSticks() {
var count = _sticks.length;
for (var i = 0; i < count; i++) {
var stick = _sticks[i];
stick.update();
}
}
function renderPoints() {
var count = _points.length;
for (var i = 0; i < count; i++) {
var point = _points[i];
point.render(drawingGraphics);
}
}
function renderSticks() {
var count = _sticks.length;
for (var i = 0; i < count; i++) {
var stick = _sticks[i];
stick.render(drawingGraphics);
}
}パラメータを変えて試してみよう
コードの解説は今回はここまでとする。後は、
makePoints(中心x座標, 中心y座標, 半径, 頂点数)
VerletStick(始点, 終点, 長さ, 固さ)function initialize() {
makePoints(100, 70, 50, 6); // 4);
}
function makeSticks() {
_sticks.push(new VerletStick(_points[i], _points[j], null, 0.5));
}前回の
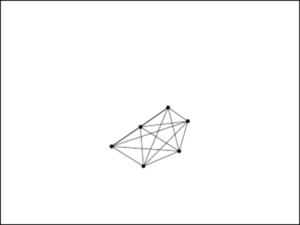
そのため、
たとえば、
var velocityY = 0.05; // 0.25;
function initialize() {
makePoints(100, 70, 50, 8);
}
function makeSticks() {
_sticks.push(new VerletStick(_points[i], _points[j], null, 0.05));
}jsdo.
![図4 jsdo.itの[Fork]と[View Diff]ボタン 図4 jsdo.itの[Fork]と[View Diff]ボタン](/assets/images/design/serial/01/createjs/0032/004.png)



