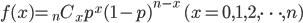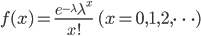今回は、前回 導入したNumpy、そしてグラフを描画するmatplotlibを使って、いくつかの代表的な分布を紹介していきます。
第5回「「よく使う分布」はどうしてよく使う? の項でも代表的な分布が紹介されていました。そこでは、“ この状況(モデル)では、この分布を使う” というパターンを想定する、それが“ よく使う分布” がいくつも存在する理由と言及されていましたが、どのような状況でどのような分布を使えばいいのでしょうか?
実際、どのような状況のときに、どのような分布を使うと説明しやすいかを考えながら、みていきましょう。
matplotlibのインストール
matplotlib はpythonとNumpyのための高機能なグラフ描画ライブラリです。今後もグラフを描画することがあるかと思いますので、ここでインストールしておきましょう。
公式サイト のダウンロードから各OS向けのパッケージを入手してインストールしてください。ソースコードからインストールする場合は、以下の手順でインストールすることができます。
svn co https://matplotlib.svn.sourceforge.net/svnroot/matplotlib/trunk/matplotlib
cd matplotlib
python setup.py build
python setup.py install
確率分布とは
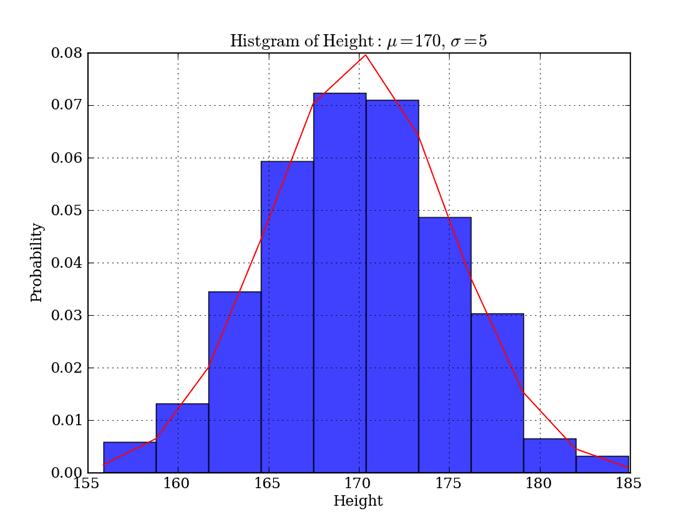
「成人男性の身長は正規分布に従う」や「空いている高速道路の料金所を1分間に通過する自動車の台数はポワソン分布に従う」などの表現を統計の本などで見たことのある人もいるでしょう。そもそも、ここで利用している分布とはどういったものでしょうか。例として成人男性の身長について考えてみましょう。健康診断などで計った身長のデータを集めて、以下のようなグラフにしてみます。
図1 身長のヒストグラムこのような表を度数分布表(ヒストグラム)といいます。このヒストグラムの形に合わせて曲線をひいていくと、山のような形になりますね。分布とはこのような曲線の形状を関数で表現し、数学的に利用するための道具になります。この“ 曲線の形状” を正規化したものが、第4回 で紹介されている確率密度関数になります。
ここで例として使った「成人男性の身長」の分布ですが非常に多くの人数の身長を測定すると、理論編で説明のあった“ 正規分布” になるといわれています。これは裏を返せば、その平均と標準偏差を持つ正規分布に従うデータを用意することができるなら、身長の疑似データが作れるということですね。そこで今回は、Numpyのrandom.normal()関数を利用して乱数を生成し、身長の疑似データとしてヒストグラムを生成してみました。この関数は第一引数に平均を、第二引数に標準偏差を与えることで、それにしたがった乱数を生成することができます。生成した乱数を利用してヒストグラムを描画するコードは次のようになります。
リスト1 ヒストグラムを描画する(histgram.py) # -*- coding:utf-8 -*-
import matplotlib.mlab as mlab
import matplotlib.pyplot as plt
import numpy as np
sample = 1000
mu, sigma = 170, 5
data = np.random.normal(mu, sigma, sample)
n, bins, patches = plt.hist(data, normed=1, alpha=0.75, align='mid')
y = mlab.normpdf(bins, mu, sigma)
l = plt.plot(bins, y, 'r-', linewidth=1)
plt.title(r'$\mathrm{Histgram\ of\ Height:}\ \mu=%d,\ \sigma=%d$' % (mu, sigma))
plt.xlabel('Height')
plt.ylabel('Probability')
plt.grid(True)
plt.show()様々な分布
冒頭でも紹介しましたが、分布にはたくさんの種類があります。分布の種類は大きく分けると、「 離散型確率分布」と「連続型確率分布」の2種類に分類することができます。さらに、離散型確率分布には二項分布、ポアソン分布、ベルヌーイ分布、多項分布などが、連続型確率分布にはガンマ分布、ベータ分布、t分布、F分布、ディリクレ分布などが含まれています。
離散型確率分布と連続型確率分布の違いについては既に説明しているので詳細な説明は省略しますが、分布の説明をするためにもここで簡単に復習しましょう。
離散した数値から成るデータでは、それぞれの数値についての確率を計算することができます。例えば、サイコロで6の目の出る回数や、ある特定の期間に機械が故障する回数、車の台数などですね。このようにデータが離散しているときには、データは特定の値しか取ることはありません。確率変数が離散値になるような分布を「離散型確率分布」といいます。
しかし、身長や時間などのいくらでも細かく測れるようなデータは特定の値を取ることは実際には0に近いですよね。このような確率変数が連続量となるような確率分布を「連続型確率分布」といいます。
離散型確率分布 連続型確率分布
二項分布、
ガンマ分布、
ここで列挙したものは代表的な分布で、実際にはここでは紹介しきれないくらいに様々な分布があります。それぞれの分布について説明すると、それだけで本が1冊書けるくらいの分量になってしまいます。そこで今回は、離散型確率分布の中から3つの分布を紹介します。
ベルヌーイ分布(Bernoulli Distribution)
正規分布を聞いたことがある人でも、ベルヌーイ分布を知っている人は少ないかもしれません。ゲームでの先攻・後攻を決めるためのコイントスや、薬が効くか効かないか、はたまた株価が上がるか下がるか…。このような1回の試行結果が「裏・表」「 効く・効かない」「 上がる・下がる」のような2つの状態しか現れない確率実験を「ベルヌーイ試行」と呼びます。そして、ベルヌーイ試行によって得られる分布を「ベルヌーイ分布」と呼びます。
試行の結果、2つの状態しか現れないということは、2つの確率 p, q からなる事象ということもできますね。確率の値は0以上1以下、すべての確率の取る値を合計すると1になるため、成功する確率を p とした時、当然失敗する確率は (1 - p) となります。これを確率質量関数で表すと次のようになります。
例として、ある病気に対する薬の効果について考えてみましょう。薬に効果のあった(成功した)場合を X=1、効果のなかった(失敗した)場合を X=0 とします。薬の効く確率を0.724とすると、P(X=1) = 0.724、P(X=0) = 1 - 0.724 となります。グラフに描画すると以下の図のようになります。
図2 ベルヌーイ分布このベルヌーイ分布は、それ単体で利用されることは少なく、ベルヌーイ分布に従う乱数生成を繰り返した時に、その乱数の性質について調べる時などに用いられます。
二項分布 (Binomial Distribution)
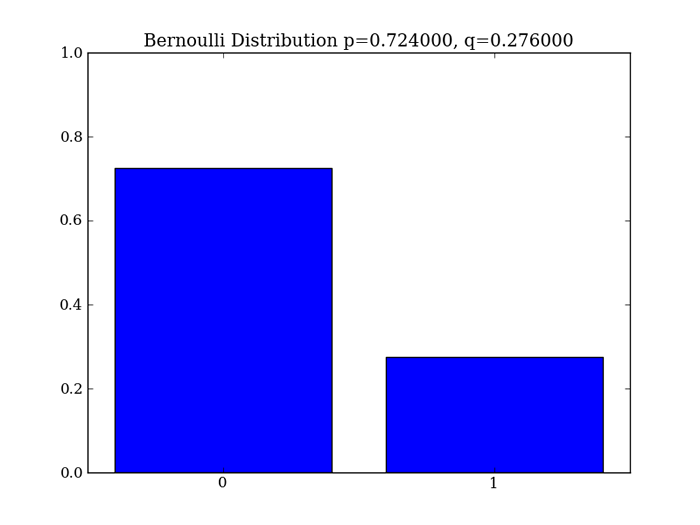
ベルヌーイ分布は1回の試行結果でした。それでは、同じように成功する確率pのベルヌーイ試行をn回繰り返したらどうなるでしょうか。このような同じ事柄を繰り返したとき、ある事柄が何回起こるかの確率分布が二項分布になります。二項分布は以下のような分布で示されます。
図3 二項分布例えば、表の出る確率をpとしたとき、n回コインを投げて最初のx回に続けて表が出て、残り (n-x) 回に裏の出る確率は
最初のx回だけではなくn回中にx回表が出るような場合はどうなるでしょう。それぞれ確率質量関数は次のように記述することができます。
試行回数を10ずつ増やしながら、コインの表面の出る確率を求めるコードは以下のようになります。binomial関数の中に先程の確率質量関数がそのまま記述されているのがわかりますね。
リスト2 二項分布のグラフを描画する(binomial_distribution.py) # -*- coding:utf-8 -*-
import matplotlib.pyplot as plt
import numpy as np
import math
def comb(n, r):
return math.factorial(n) / (math.factorial(n - r) * math.factorial(r))
def binomial(p):
def f(n, x):
prob = comb(n, x) * p ** x * (1 - p) ** (n - x)
return prob
return f
p = 0.5
L = []
trial_count = (10, 20, 30, 40, 50)
colors = ["r", "g", "b", "c", "y"]
f = binomial(p)
for n in trial_count :
L.append([f(n, x) for x in range(n)])
for prob, color in zip(L, colors) :
plt.plot(prob, color)
ax = plt.axes()
ax.set_xlim(0, 50)
ax.set_ylim(-0.05, 0.3)
plt.title(r'$\mathrm{Binomial Distribution}\ P=%f$' % (p))
plt.xlabel('Trial')
plt.ylabel('Probability')
plt.legend([str(n) for n in trial_count])
plt.show()ポアソン分布(Poisson Distribution)
1時間あたりの交通事故が発生する確率や、1ページの文章を書いたときに綴りを間違える確率のような、稀に起こる事象の分布が「ポアソン分布」です。滅多に起こることのない事象の確率分布であることから、別名「少数の法則」とも呼ばれています。歴史的に有名なポアソン分布が利用された事例としては、戦争で馬に蹴られて死んでしまう兵士の発生件数の調査があります。馬に蹴られて死んでしまうなんて滅多に起こらないですよね。ポアソン分布を確率質量関数で表すと次のような式になります。
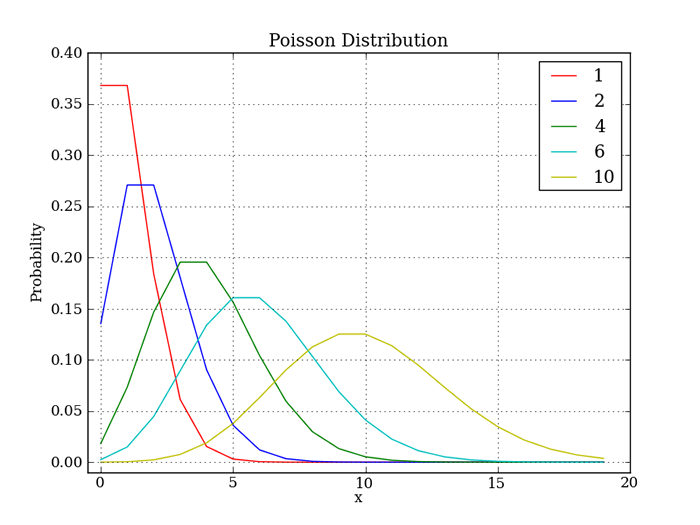
この分布は平均(λ)の値だけで決まり、グラフは次のような形になります。凡例にある数字が入力された平均値です。
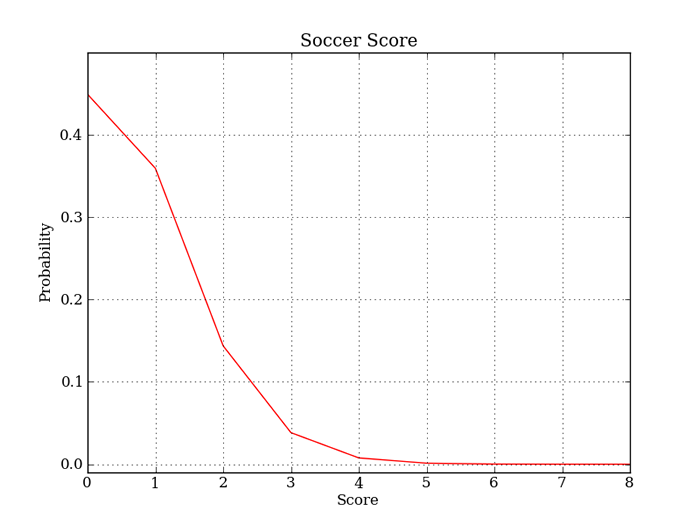
図4 ポアソン分布例として、1試合に平均得点が0.8点のサッカーチームがあったとします。そのチームの1試合の得点の確率分布をみてみましょう。グラフに現わすと次のような形になります。1試合の中では0点で終わる確率がもっとも高く、2点目を獲得するあたりから極端に確率が低くなっているのがわかりますね。4点目になるとほぼ0に近い確率になってしまいます。
図5 サッカーの1試合における得点の確率分布このグラフを描画しているコードでも、先程紹介した確率質量関数を実直に実装しています。
リスト3 サッカーの1試合における得点の確率分布を描画する(soccer_score.py) # -*- coding:utf-8 -*_
import matplotlib.pyplot as plt
import numpy as np
import math
def poisson(lambd):
def f(x):
return float(lambd ** x) * np.exp(-lambd) / math.factorial(x)
return f
N = 8
L = []
score_mean = 0.8
f = poisson(score_mean)
L.append([f(k) for k in range(N + 1)])
for prob in L:
plt.plot(range(N + 1), prob, 'r')
ax = plt.axes()
ax.set_xlim(0, N)
ax.set_ylim(-0.01, 0.5)
plt.title('Soccer Score')
plt.xlabel('Score')
plt.ylabel('Probability')
plt.grid(True)
plt.show()まとめ
今回は離散型確率分布の中から3つの分布を紹介しました。連続型確率分布でも標本が小さい時に有効なt分布や、PERT(Program Evaluation and Review Technique)という工程計画で用いられるベータ分布などがあります。今回紹介できなかった分布も今後の連載の中で紹介する機会があると思うので楽しみにしていてください。
次回の理論編は、線形回帰と正則化項の説明になります。やや難しい内容になるかもしれませんが、重要な内容ですので頑張りましょう。
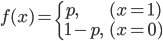
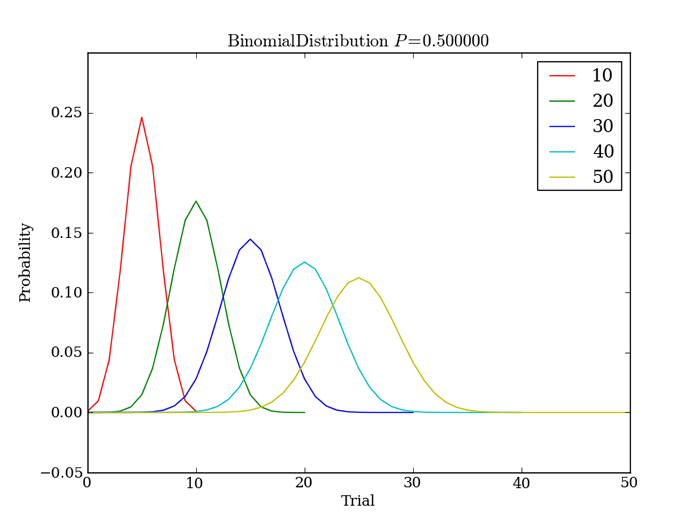
![]() になりますね。これが、
になりますね。これが、![]() 通りの中で、
通りの中で、![]() の確率で起こるため、
の確率で起こるため、