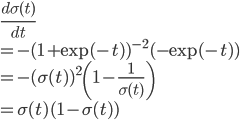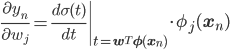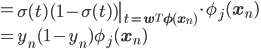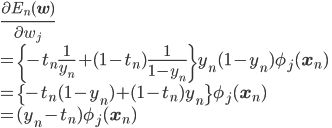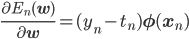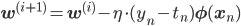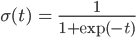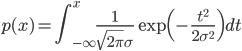次の式でパラメータを更新していきます。
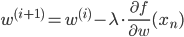
w(i)はi回目の更新をしたパラメータ、λは適当な正の値で、iが増えるにつれて小さくしていきます。
確率的勾配降下法は、勾配さえ得られればとても簡単に実装ができ、高速に解を求められるという特徴があります。しかも大規模データに対して適用しやすいため、特に最近は好んで利用される傾向にあります。また、局所解に捕まりにくいというメリットもなかなか見逃せません。
あれあれ、なにやらいいことずくめのような書き方になってしまいましたね。
念のため注意しておくと、どのような問題に対しても高速で局所解に捕まりにくい、というわけでは決してありません。問題によっては確率的勾配降下法より良い最適化手法があるでしょう。解きたい問題や求めたい解にあわせて手法を選ぶ必要があるという点は忘れずにいたいですね。
ロジスティック回帰の学習
では、確率的勾配降下法を使ってロジスティック回帰の学習手順を導きましょう。
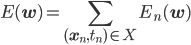
ただし、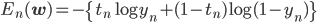 、
、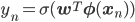
確率的勾配降下法で負の対数尤度関数E(w)を最適化するには、訓練データの各点に対応するEn(w)の勾配が必要です。
勾配は各成分方向での偏微分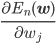 を並べたベクトルですから、この偏微分を計算しましょう。
を並べたベクトルですから、この偏微分を計算しましょう。
この連載では基本的に途中の計算過程を省いていましたが、実はロジスティック回帰は勾配が簡単に書けることが最大のポイントであるため、今回は少し丁寧に式展開します。
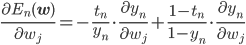
ここで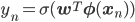 の微分をきれいに片づけるために、ちょっとしたテクニックを使います。
の微分をきれいに片づけるために、ちょっとしたテクニックを使います。
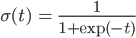
より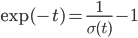 ですから、
ですから、
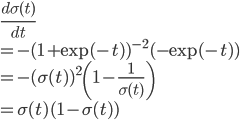
と、σ(t)の微分をあえてσ(t)を使って表します。
すると、
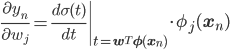
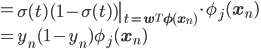
ynの微分をシンプルな形に書き下すことができました。
これを元の式に代入すると、
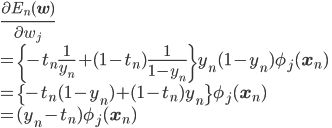
うまく行き過ぎ、と言いたくなるくらい簡単になりましたね。
勾配は各wjごとの偏微分を束ねたベクトルであることを思い出すと、最終的にEn(w)の勾配は次のようになります。
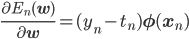
よって学習率をηとすると、確率的勾配降下法によるパラメータの更新式は次のように書けます。
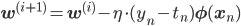
確率に変換する関数
ロジスティック回帰のパラメータの更新式が導出されましたので、その学習の実装ができるようになりました。
その実装は実践編に譲り、ここでは初心にかえって、ロジスティック回帰は「シグモイド関数の出力を確率と見なす」という仮定から出発したことを改めて思い起こしてみましょう。
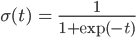
この肝心の式がどうも確率っぽくないんだよなあ、というのが最初からの疑問としてありましたね。
そういえば名前の「ロジスティック」も「兵站」などという意味、つまり軍隊のような大勢の人間が関わる計画のために必要なことを指す言葉であり、やはり確率っぽくありません。
この疑問に目をつぶって学習手順を導出してきましたが、気持ちよく実装するためにも、いよいよこの疑問に正面から立ち向かってみることにしましょう。
そもそも、シグモイド関数のようによくわからない関数ではなく、ちゃんと確率っぽい「0から1までの確率に変換する関数」ってないのでしょうか? そういう関数があるなら、それを使えばいいですよね。
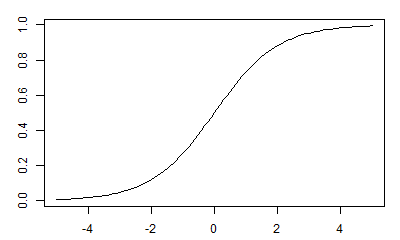
実際、そういう関数はきちんとあります。中でも有名なものは正規分布の「累積密度関数」です。
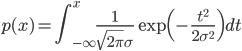
「累積密度関数」とは確率密度関数を-∞からxまで累積、つまり積分したもので、要は「x以下の値をとる確率」の関数です。
連載第4回で話したように、確率密度関数の値は確率ではなく、その値が1より大きくなることもあるのでした。
一方の「累積密度関数」は確率密度関数を積分したものですから、その値は確率です。したがって0から1の間に必ず入り、単調増加で(累積ですからね!)、xが小さくなれば値は0に近づき、大きくなれば1に近づくという、いろいろな性質があらかじめわかっている関数なのです。
しかも確率密度関数がほしくなったら累積密度関数を微分すればよく、また区間 [a, b] に入る確率を求めたければ p(b)-p(a) を計算すればよい、など細々と役に立ちます。
そして、もっとも代表的な分布といえる正規分布なら由緒正しさは折り紙付きですから、その累積密度関数を「確率に変換する関数」として使えば、その確率らしさに疑問の生じる余地などありませんね。
これで新しくすばらしいモデルができそう……と、ぬか喜びしたところ申し訳ないですが、そういうモデルはすでにあり、「プロビット回帰」という名前もついてます。「プロビット」は"probability unit"を短縮したものなので、名前からして確率していますね。
ではなぜ清く正しい「プロビット回帰」を勉強しないのでしょう。
先ほどの正規分布の累積密度関数p(x)の式を見てください。シグモイド関数の代わりにするということは、この計算できない積分の入った式を対数尤度に代入して、その勾配を求めるということです。想像しただけでうんざりします。
これを解くには面倒な計算といくつもの工夫を重ねて、ようやく近似解を求めるという流れになります。機械学習は「計算できることが正義」なので、どれほど由緒正しく優れたモデルであったとしても、計算が大変では嬉しくないです。
さてはて、どうしたものでしょうか。
後から解くときに近似をするくらいなら、確率に変換する関数として「正規分布の累積密度関数に十分よく似た、その後の計算が楽な関数」を使ってしまうという手はどうでしょう。
そういえば、グラフを見せるのをうっかり忘れてましたね。次の図の青い線が正規分布の累積密度関数です。
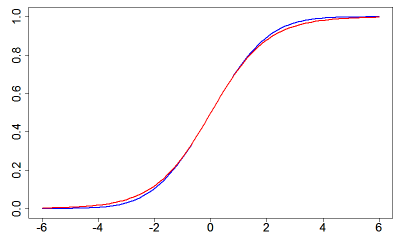
正規分布の累積密度関数と見るからにとてもよく似た赤い線は、人口増加を記述するモデルのために作られた関数で、最初は指数的に増加していき、あるところから増加率が減少、最終的にはある値で頭打ちになるという振る舞いをするものです。
この関数はとてもシンプルな式で書け、しかも勾配の計算もおそろしく簡単という特徴も持っていたことから、先ほど考えていた「正規分布の累積密度関数によく似た、その後の計算が簡単な関数」として、これ以上ないくらいぴったり適任です。
ちなみにこの関数は人口を表現する目的から「ロジスティック関数」と呼ばれていたため、これを使って構成された「プロビット回帰の簡単計算版モデル」は「ロジスティック回帰」と名付けられました。難点があるとすれば、もともと確率と関係ない関数だったこと……。
この「ロジスティック関数」は、この連載で「シグモイド関数」と呼んでいた関数に他なりません。
もともと「シグモイド」とはS字のカーブのことで、本来「シグモイド関数」とはグラフがそのような形の関数の総称です。例えば正規分布の累積密度関数もシグモイドですし、他にはarctan(tanの逆関数)なども当てはまります。
しかし多くの文脈、特にロジスティック回帰の場合は、ロジスティック関数 σ(t)=1/(1+exp(-t)) を単に「シグモイド関数」と呼んでいます。
まとめると、ロジスティック回帰は元祖であるプロビット回帰を計算しやすいように崩したものなので、確率的な根拠が薄く感じるのは由来からして当然だったのです。
その点について、ロジスティック回帰が提案された当時は今よりずっと強く批判されていたようですが、現在は対数線形モデルとの関連などの理屈付けもさることながら、なによりその有用性によって認められています。
次回は実践編として、ロジスティック回帰を確率的勾配降下法で解くのを実装してみましょう。お楽しみに。
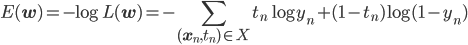
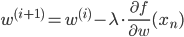
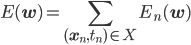
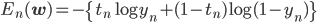 、
、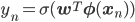
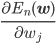 を並べたベクトルですから、
を並べたベクトルですから、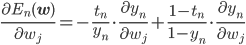
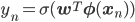 の微分をきれいに片づけるために、
の微分をきれいに片づけるために、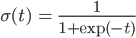
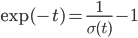 ですから、
ですから、