連載第1回が掲載された2010年の6月から，休み休みながらも足かけ3年続いてきたこの『機械学習 はじめよう』も今回が最終回です。

21回にわたる連載の最後を飾る今回は，ここまでの流れの中では触れられなかった「機械学習で実用的なアプリケーションを作るときに気をつけたいこと」を中心にいくつかまとめます。

未知のデータへの対応能力

第9回で「過学習」について少し紹介しました。簡単に復習すると，「⁠過学習」とはモデルが「訓練データさえ正解になればいい」と状態になってしまうことで，未知のデータ（訓練データに含まれない，モデルが知らないデータ）に対する結果がデタラメになりがちという困った特徴があります。

しかも都合の悪いことに，モデルの表現力が高い（パラメータが多く，色々な分布を表すことができる）ほど過学習になりやすいことがわかっています。

そんな困った過学習を防ぐ方法の1つは，期待した答えのみが得られるモデルを使うというものです。例えば，欲しい答えが3次多項式とわかっていれば，モデルを最初からその範囲に限定しておくという実に直接的なアプローチです。

解く前から答えに見当がついている場合には最も確実で効果も高いのですが，汎用的な方法とは言い切れません。

もう少し汎用的な手法として，第9回や第13回でも紹介した「正則化」があります。

過学習が起きているときには，パラメータが3桁や4桁もあるような極端な値になってしまっていることが多いです。モデルのパラメータに極端に大きい値があると，入力データが少し変わっただけで得られる結果がガラリと変わってしまいますから，「⁠似ているデータからは似ている結果が出る」という直感にも反します。

そこで，「⁠パラメータが0から離れるほどペナルティを与える，つまりパラメータが極端な値になりにくくする」ことで過学習を抑制するのが正則化でした。

復習はこれくらいにしておいて，ここでは今あるモデルが過学習を起こしているか（起こす可能性があるか）を知る方法について少し考えてみましょう。そもそも過学習を起こしていなければ対策の必要がなくて助かりますからね。

過学習とは未知のデータに対する予測を間違うことですから，訓練データに含まれない「テストデータ」を十分用意して，その予測の正解率を見るのが過学習を判定する王道でしょう。

しかしがんばってテストデータを用意しても，「⁠その訓練データとテストデータの組で過学習的現象が起きるか」はわかりますが，他の組み合わせでも大丈夫かまではわかりません。

テストデータを増やせば増やすほどその心配を減らすことができますが，そのためのデータを用意する作業は非常に高コストです。手前味噌で恐縮ですが，言語判定器を作るためにテキスト（Twitterのツイート）に「どの言語で書かれたものか」というラベルをつける作業を行いましたが，それには何ヶ月もかかっています。しかもこれは，正解付け（アノテーション）の中では最もやさしい部類なのです。ここでは詳細は省きますが，性能向上のためのパラメータチューニングに使う「開発データ」を別に用意するとなるとさらにデータが必要になったりします。

いやいや，そんな湯水のように正解つきデータが出てくるなら，むしろ全部訓練データに回したいところです。過学習とは訓練データだけが正解になる困った現象ですが，その訓練データがありとあらゆるデータを含んでくれていれば，「⁠訓練データだけが正解」でも十分ですよね。現実にはそこまで単純な問題ではないのですが，巷で噂のビッグデータが嬉しいのはこういったことも本質的に関係しています。

しかし残念ながらそんな嬉しいことは起きるわけがないので，貴重で高価な正解つきデータはもう少し節約しながら，モデルが過学習を起こしそうかどうかについて知る方法はないでしょうか。

そのための方法の一つが「交差検定」です。「⁠検定」という名前がついていますが，統計にあるカイ二乗検定などとは全く違うものです。「⁠交差検証」とも呼ばれます。

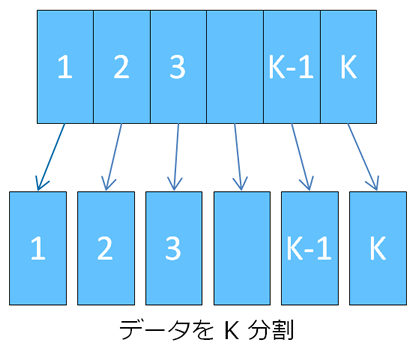
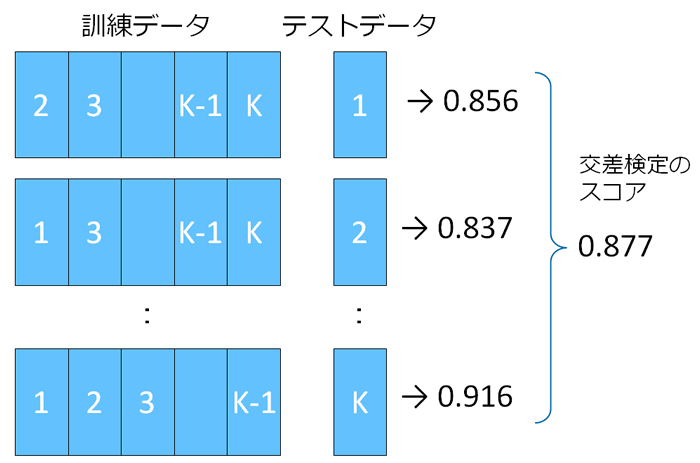
交差検定のやり方はいくつかありますが，最もポピュラーな「K-分割交差検定」を紹介しましょう。これは，正解付きのデータをK分割して，そのうち1つをテストデータに，残りのK-1個を訓練データとして学習と精度の評価を行います。これをK個のデータのかたまりに渡って順に，つまり学習と評価をK回行って，その結果を平均したものを「未知のデータへの対応能力」とする方法です。

こうした「未知のデータへの対応能力」はそのモデルの性能と考えられ，特に「汎化性能」とも呼ばれます。複数のモデル候補の中から最も性能の高いモデルを選ぶ事を「モデル選択」と言います。

ここでは詳しく述べませんが，モデル選択には他にも各種情報量基準などを使う方法もあります。その中での交差検定の強みは，手持ちのデータを最大限まで活かした性能測定ができることですが，モデルの学習をK回行うという仕組みからも明らかに，計算時間がかかってしまうという難点もあります。Kを増やすほど信頼度も上がるのでますます悩ましいです。

どんなモデルを使用するかは完全に人の手にゆだねられており，アプリケーションの出来不出来はそれ次第でかなり決まってしまいます。良い機械学習アプリケーションを作るためには，より適切なモデルを選択することが大切です。

きれいなモデルと汚いデータ

機械学習の確率モデルのほとんどは，データが「独立同分布」（⁠independent and identically distributedの頭文字を取り，i.i.d.とも表されます）に従うことを仮定しています。これは「同じ分布から独立に⁠」⁠，つまりある不変な真のデータ分布があって，観測されるデータはそこから独立に（並ぶデータと関連なく）得られるという意味です。

尤度が確率の掛け算で表せるのは，まさに独立同分布のおかげです。逆に，独立同分布がないと尤度をそんなに簡単には書き下せないわけで，問題を解くのが非常に難しくなるでしょう。

しかし現実のデータは，独立同分布に従うそんなきれいなデータなのでしょうか。

まず，単純な入力ミスや，センサーの測定限界などのために一部の項目の値がないデータ（欠損値）や他に類似した値のないデータ（外れ値）が含まれているということは十分考えられます。これらは分布に従わないノイズデータであるため，「⁠同分布」の仮定から外れています。

実用的な機械学習アプリケーションでは，そうしたノイズへの対策のためにデータクリーニングや正規化といった前処理が大変重要な役割を果たします。しかし，その具体的な処理の内容はアプリやデータによって全く異なるため，機械学習一般を扱うこの連載では泣く泣く省略します……。

一方，「⁠独立」の仮定はどうでしょう。よく例題などでも使われる身長のデータは，同じ人種・血縁や同じ地域の人間の間で相関が出るでしょうし，試験の点数などのデータも一緒に勉強した友達同士は無関係な学生より相関が高そうです（山が当たったりした場合は特に顕著に表れそうですよね⁠）⁠。

データが本来持っているこういった偏りを計算のために無視することは，ある種の理想化したきれいなモデルを，現実のデータに当てはめるものです。ただ計算のためだけにモデルを勝手に理想化してもいいのだろうか，というのは当然の疑問でしょう。

しかし，現実により近いモデルを使ったら計算できなくなった，なんてことになったらまさに本末転倒です。この連載で何度か言及しているように「機械学習は計算できることが正義」なのです。

そして，理想化されたシンプルなモデルを使うのは，計算量以外にももう一つ大きな理由があります。

現実のデータを使って機械学習アプリケーションを作ろうとすると，モデルを一回学習したら文句のつけようのない結果が得られて終わり，なんてことはまずありません。望む結果が得られるまでパラメータや入力データを調整しながら何度も繰り返すことになります。そのとき，こういうデータを入れたらこういう結果になるだろう，このデータを追加したらこれくらい精度が良くなるだろうというように，制御しやすいモデルが大変使い勝手の良いモデルだということは想像しやすいでしょう。

モデルが複雑になればなるほど，そういった制御は当然難しくなっていきます。シンプルできれいなモデルはこのような面でもメリットが大きいのです。

また，なんらかの機械学習のモデルを使って得られた結果に対して，なぜこうなったのか説明がほしいと言われることもあります。機械学習でブラックボックスだからわかりませんというわけにもいきません。

そういうとき，実はモデルによってそういう「説明がしやすいもの」と「しにくいもの」とがあります。ここでも詳細は省きますが，もうこの後の展開は予想できるでしょう。ここでもやはりシンプルなモデルほどそういった説明をしやすい傾向にあるわけです。

と，ここまできれいなモデルを正当化する話ばかりしてきましたが，最終的にはコストパフォーマンスの問題に落ち着きます。つまり，現実のデータに寄りそった計算が大変なモデルでも，人間の目から見ても明らかに良い成果が出ることがわかれば使われるようになるでしょう。

機械学習を使う立場の人間としては，このモデルは使える使えないという思い込みに縛られずに，幅広いモデルの中から目的に適したものをバランスよく選ぶことを心がけたいものですね。