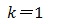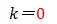お詫びと訂正（正誤表）

本書の以下の部分に誤りがありました。ここに訂正するとともに，ご迷惑をおかけしたことを深くお詫び申し上げます。

P.24，P.100　例題10-1　の問題文2行目

誤	Φ（6）＝1
正	Φ（6）＝2

別冊
P.32 　発展演習2 解答　下から2行目

誤
正

（以下，2016年12月12日更新）

本冊
P.44　解答　Ⅰ（１）（ii）の3行目～4行目

誤	(y,z)＝(1,5), (2,3) (3,1)　（i）(ii)から（x,y,z）は6組
正	(y,z)＝(1,5)　 （i）(ii)から（x,y,z）は4組

P.57　演習4-3　問題文中

誤	2n+1
正	2n+1

P.86　解答1 下から3行目～2行目

誤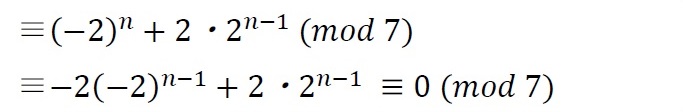
正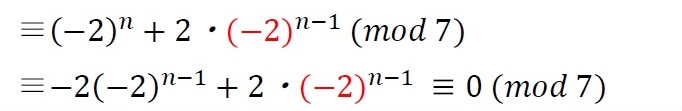

別冊
P.2　解答　Ⅳ　下から2行目

誤	(a,b)=(1,2)
正	(a,b)= (2,1)

P.6　解答　Ⅱ　上から5行目

誤	p<q
正	p≦q

P.12　演習4-3　問題文中

誤	2n+1
正	2n+1

P.17ページ　演習6-2　Ⅱ　解答

下記のように，差し替えます

正	q＝2のとき、それぞれ2、5、７、11、17となり題意を満たす。　…① (i) q≡0(mod 5)のとき、5数のうちq≡0(mod 5） (ii) q≡1(mod 5)のとき、5数のうち6q－1≡0(mod 5） (iii) q≡2(mod 5)のとき、5数のうち2q＋1≡0(mod 5） (iv) q≡－2 (mod 5)のとき、5数のうち8q＋1≡0(mod 5） (v) q≡－1(mod 5)のとき、5数のうち4q－1≡0(mod 5） (i)～（v）より、すべての自然数qで、q、2q＋1、4ｑ－1、6q－1、8q＋1のいずれかが5の倍数となる。…② ①、②より、題意を満たすqは2と5である。