サポートページ
ダウンロード
(2022年5月10日更新)
「実力アップ模試」の解答・解説
巻末の別冊付録「実力アップ模試」の解答・解説をこちらからダウンロードできます(PDFファイル)。
なお、内容に一部修正が入りましたので、更新しました。2022年5月10日以前にダウンロードされた方は、お手数ですが再度ダウンロードしてください。
「試験によく出る用語マスター」をお使いいただくために
本書をお買い上げいただいた読者様には、試験によく出題される重要用語をマスターするための付録「試験によく出る用語マスター」をこちらからダウンロードできます。
「試験によく出る用語マスター」はPDF形式のファイルとなっています。ご利用の際は「Adobe Acrobat Reader」アプリが必要です。下記のリンクから、Apple Store(iPhone/iPad)/Playストア(Android)/ダウンロードサイト(パソコン)が開くので、各自でインストールしてください(インストール済みの方は次に進んでください)。
Adobe Acrobat Readerを入手する
https://
「試験によく出る用語マスター」のダウンロード
「試験によく出る用語マスター」をダウンロードするには、本書の表2(表紙の裏)に掲載されているIDとパスワードを入力して、ダウンロードボタンを押してください。
Adobe Acrobat Readerで表示する方法
ファイルダウンロード後に、Adobe Acrobat Readerで「試験によく出る用語マスター」を表示する方法を案内します。また、便利にお使いいただくために、「単一ページ」表示をお薦めしております。その切り替え操作も紹介します。
※以下のリンク先 では「IT パスポート・試験によく出る用語マスター」の画面を例に解説 していますが、「基本情報技術者・試験によく出る用語マスター」でも操作方法は同様です。
- iPhone/iPadの場合
- Androidの場合
- パソコンの場合
ダウンロードしたPDFファイルをダブルクリックすれば開くことができます。
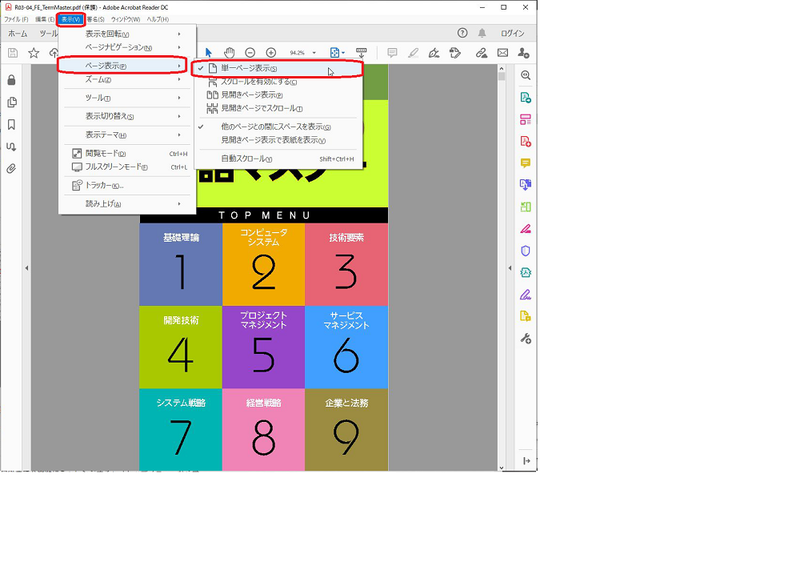
パソコンでも「単一ページ」表示でご利用いただくのがお薦めです。メニューから[表示]-[ページ表示]-[単一ページ表示]を選択することで切り替わります。
図 単一ページ表示への切り替え(パソコン版)
全用語を順番に学習したい方へ
「試験によく出る用語マスター」はPDF形式のファイルですので、ページをめくる操作(左右にスワイプ、マウスでのスクロール操作など)でも「質問」→「答え」の順に次々と学習を進めることができます。
「最初から最後まで全問題にチャレンジする」「トップメニューから学習したい章に飛んで、その章の全問題にチャレンジする」など、網羅的に学習を進めたい方におすすめです。
お詫びと訂正(正誤表)
本書の以下の部分に誤りがありました。ここに訂正するとともに、ご迷惑をおかけしたことを深くお詫び申し上げます。
(2021年4月23日最終更新)
第2訂正情報
P.45 表中の「Zigbee」の解説
| 誤 | 十数m程度を想定した短距離赤外線通信規格。 |
|---|---|
| 正 | 十数m程度を想定した短距離無線通信規格。 |
第1刷訂正情報(第2刷では修正済み)
P.008 冒頭のイラスト「②工夫すれば単純な計算になる」2行目
| 誤 | 256=2の7乗だから…… |
|---|---|
| 正 | 256=2の8乗だから…… |
P.010 「掛け算は左シフト、割り算は右シフトで行える」の囲み部分
| 誤 | 左にnビットシフト →元の数値の2n倍になる …nが2なら、2×2 |
|---|---|
| 正 | 左にnビットシフト →元の値の2n倍になる …nが2なら、22=4倍(4を掛けた値) |
| 誤 | 右にnビットシフト →元の数値の2-n倍になる …nが2なら、2÷2 |
|---|---|
| 正 | 右にnビットシフト →元の値の2-n倍になる …nが2なら、2-2=1/22=1/4倍(4で割った値) |
P.011 「無限小数の判定問題」の一番下の行
| 誤 | 《無限小数の例》10進数0.2は、2進数0.0011001100… と同じ値が繰り返される。 |
|---|---|
| 正 | 《無限小数の例》10進数0.2は、2進数0.001100110011… と同じ値が繰り返される。 |
P.012 「2のべき乗の組み合わせを見つけ出そう」の解説「解答のワザ」2~3行目
| 誤 | 次の方法は、基数が2なら小数に2を掛け、整数部を並べていきます。 |
|---|---|
| 正 | 下記は10進小数を2進小数に変換する方法で、基数の2を掛けていき、整数部を順に並べます。 |
P.012 「○負数は2の補数で表現する」の解説の1行目
| 誤 | まず、符号ビットを含めたすべてのビットを反転します |
|---|---|
| 正 | 負の数は2の補数を使って表現します。求め方は、まず符号ビットを含めたすべてのビットを反転します |
P.013 浮動小数点形式の図を変更
| 誤 | 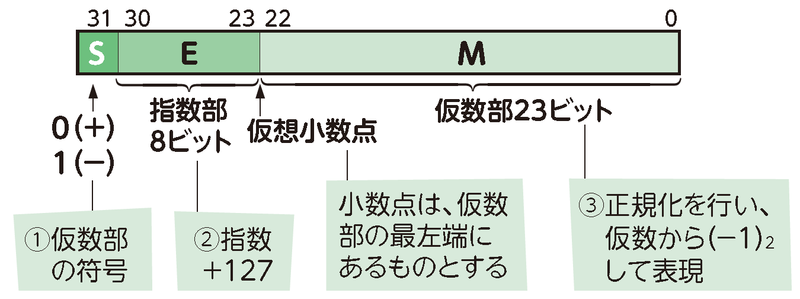 |
|---|---|
| 正 | 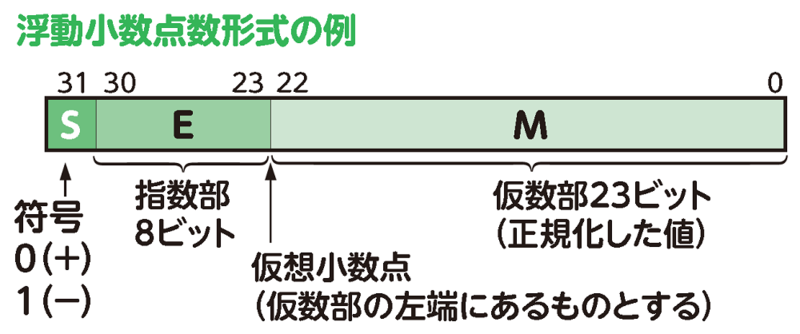 |
P.013 「正規化」の解説
| 誤 | 実数を表現する際、例えば0.123×101でも、0.0123×102でも値は同じです。ただし後者の表現では、前者よりも仮数部の桁数は多く必要になります。精度が求められる計算では桁数が重要になるため、桁数をできるだけ稼ぐため仮数部の最上位桁を0以外になるように調整します。これを正規化といいます。 |
|---|---|
| 正 | 実数を表現する場合に、例えば、0.0123×102でも、0.123×101でも値は同じです。ただし前者の表現は、後者よりも仮数部の桁数が多く必要になります。精度が求められる計算では桁数が重要になることから、桁数をできるだけ稼ぐために仮数部の最上位桁が0以外になるよう小数点位置を調整します。これを正規化といいます。 |
P.013 試験問題の例「2の補数表現による表現範囲を思いだそう」の解説を差し替え
| 誤 | →前ページの表からもわかるように、符号付きの固定小数点方式では-128が最大の絶対値。16進数は2進数を4桁ずつ区切った形なので、先頭の1ビットのみ“1”で後は“0”となっている8000が正解。 |
|---|---|
| 正 | →前ページの図からもわかるように、負数を2の補数で表す方式では、先頭の1ビットのみが“1”で、後は“0”となっているビット列が絶対値の最大。16進数は2進数を4桁ずつ区切った形なので、8000が正解。 |
P.013 表組み中の用語「桁落ち」の解説を差し替え
| 誤 |
絶対値のほぼ等しい2つの数値を減算したときに、有効桁数が急激に減少し、それによって発生する誤差。左の方法のように、計算過程の工夫で軽減できる。 例)18.6645-18.6641 =0.0004では、有効桁数6桁が1桁になっている |
|---|---|
| 正 |
絶対値のほぼ等しい2つの数値を減算したときに、有効桁数が急激に減少することで発生する誤差。 例)18.6645-18.6641=0.0004では、有効桁数6桁が1桁になっている。 |
「左の方法のように、計算過程の工夫で軽減できる。」を削除
P.013 表組み中の用語「情報落ち」の解説を差し替え
| 誤 | 絶対値の差が非常に大きい2つの数値の加減算を行ったとき、絶対値の小さいほうの値が有効桁数内に収まらず、演算結果に反映されないため発生する誤差。 |
|---|---|
| 正 | 絶対値の差が非常に大きい2つの数値の加減算を行ったとき、絶対値の小さいほうの値が有効桁数内に収まらず、演算結果に反映されないため発生する誤差。計算過程の工夫で軽減できる(左欄外の「情報落ちを防ぐ方法」を参照)。 |
P.013 側注「情報落ちを防ぐ方法」の解説を差し替え
| 誤 | 情報落ちは、絶対値の差が要因なので、まず絶対値の小さい順に数値を並べ替えて絶対値の差のない数値どうしの演算を先に行い、ある程度の大きさになってから絶対値の大きな値を加減すると誤差を減らせる。 |
|---|---|
| 正 | 情報落ちは、絶対値の差が要因。そこで、まず絶対値の小さい順に数値を並べ替えて絶対値の差が小さい数値どうしの演算を行う。ある程度の大きさになってから絶対値の大きな値を加減算すると誤差を減らせる。 |
P.014 「基本演算」の「②AND(論理積)」
| 誤 | 両方が1(真)のとき、1(真)になります。 |
|---|---|
| 正 | 両方が1(真)のときのみ、1(真)になります。 |
P.015 「論理式の法則に慣れよう」の「基本則」の右端の色文字部分
| 誤 | →基本則においては、Aは、0または1をとると考えよう |
|---|---|
| 正 | →Aに、0または1を入れて、前ページの真理値表で確かめよう |
P.015 試験問題の例「共通項に目を付けて、分配法則を適用していこう」の解説の1行目と3行目
| 誤 | ……目をつけて分配法則を適用すると、 |
|---|---|
| 正 | ……目をつけて分配則を適用すると、 |
P.015 試験問題の例「共通項に目を付けて、分配法則を適用していこう」の解説の4行目
| 誤 | ここで論理和の法則から、B+B=1なので、C・(A+A)=C が解答 |
|---|---|
| 正 | ここで、基本則からB+B=1なので、C・(A+A)=C・1=C |
P.016 試験問題の例「桁をずらしながら、4ビットずつ取り出していけばよい」の解説の(2)(3)
| 誤 |
(2)次の桁(4ビット)を取り出すため、nを右に4ビット論理シフトする。 (3)(1)で得られたxをスタックにプッシュ(格納)する。という手順を4回繰り返す。正解はイ。 |
|---|---|
| 正 |
(2)(1)で得られたxをスタックにプッシュ(格納)する。 (3)次の桁(4ビット)を取り出すため、nを右に4ビット論理シフトする。 という手順を4回繰り返す。正解はイ。 |
※(2)と(3)の順番が逆でした。
P.223 「実力アップ模試 解答」
| 誤 | 問2 エ |
|---|---|
| 正 | 問2 イ |
(以下2021年3月5日更新)
P.009 「図解で攻略! 小数点以下の「桁の重み」は分数にする」の図中 右上
| 誤 | 2進数 0.111 |
|---|---|
| 正 | 2進数 0.1111 |
P.096 下から2-3行目
| 誤 | …57は、2進数“00011101”であり、……、“00011111”=59です |
|---|---|
| 正 | …57は、2進数“00111001”であり、……、“00111011”=59です |