前回の第20回
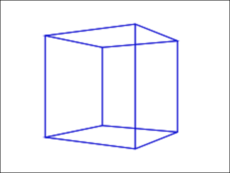 →
→

面の塗り順をどう扱うか
3次元空間でオブジェクトを描く順序については、
実は、
- 閉じた凸の多面体
- 面の裏は決して見えない
- 表向きの面は重ならない
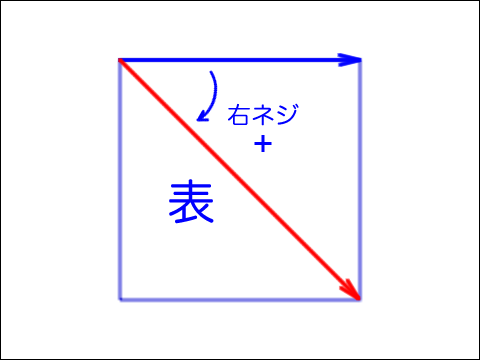
2次元ベクトルの外積で面の裏表を調べる
そこで、
ベクトルは大きさと向きをもつ。けれど、
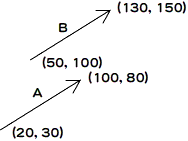
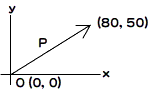
2次元平面の位置ベクトルA(ax, ay)とB(bx, by)の外積はA×Bで表し
- 2次元ベクトルA(ax, ay)とB(bx, by)の外積
- A×B =axby - aybx
ここで覚えていただきたいのは、
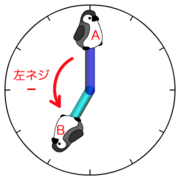
では、
実はこのために、
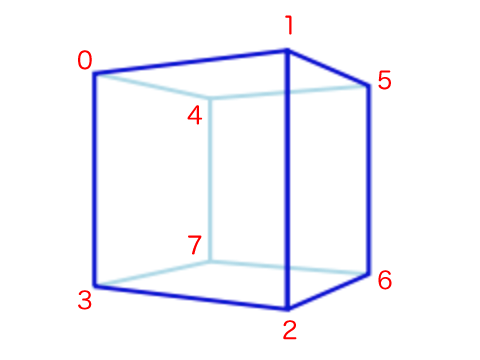
function getFacesVertices() {
var vertices = [
new Face(0, 1, 2, 3),
new Face(1, 5, 6, 2),
new Face(4, 0, 3, 7),
new Face(5, 4, 7, 6)
];
return vertices;
}
表向きの面のふたつのベクトルの位置関係を右ネジに定めれば、
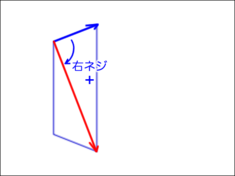
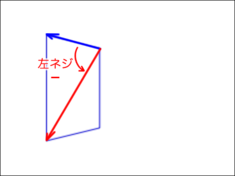
立方体の表向きの面のみを塗る
まずは、
// Face
// function Face(pos0, pos1, pos2, pos3) {
function Face(pos0, pos1, pos2, pos3, color) {
this.length = 4;
this.color = color;
this[0] = pos0;
this[1] = pos1;
this[2] = pos2;
this[3] = pos3;
}
// MathUtils
var MathUtils = {};
MathUtils.getRandomInt = function(min, max) {
if (min > max) {
var temp = min;
min = max;
max = temp;
}
var randomNumber = Math.random() * (max - min) + min;
return Math.floor(randomNumber);
};面のクラス
function getFacesVertices() {
var vertices = [
/*
new Face(0, 1, 2, 3),
new Face(1, 5, 6, 2),
new Face(4, 0, 3, 7),
new Face(5, 4, 7, 6)
*/
new Face(0, 1, 2, 3, getRandomColor()),
new Face(1, 5, 6, 2, getRandomColor()),
new Face(4, 0, 3, 7, getRandomColor()),
new Face(5, 4, 7, 6, getRandomColor())
];
return vertices;
}
function getRandomColor() {
return createjs.Graphics.getRGB(Math.floor(MathUtils.getRandomInt(0, 0xFFFFFF)));
}そして、
function drawFaces(points, faces) {
var facePoints = face.getFacePoints(points);
// draw(facePoints);
draw(facePoints, face.color);
}
// function draw(points) {
function draw(points, color) {
drawGraphics
// .beginStroke("mediumblue")
// .setStrokeStyle(1)
.beginFill(color)
.moveTo(point.x, point.y);
}これで、
外積を計算するには、
MathUtils.subtractVectors = function(vector0, vector1) {
var vectorX = vector1.x - vector0.x;
var vectorY = vector1.y - vector0.y;
return new createjs.Point(vectorX, vectorY);
};
MathUtils.crossProduct2D = function(vector0, vector1) {
return vector0.x * vector1.y - vector0.y * vector1.x;
}立方体を描く関数
function drawFaces(points, faces) {
if (isFront(facePoints)) {
draw(facePoints, face.color);
}
}
function isFront(facePoints) {
var origin = facePoints[0];
var vector0 = MathUtils.subtractVectors(origin, facePoints[1]);
var vector1 = MathUtils.subtractVectors(origin, facePoints[2]);
return (0 これで、


書上げたJavaScriptコードを以下にまとめよう。まずは、
// Point3D
function Point3D(x, y, z) {
this.x = x;
this.y = y;
this.z = z;
}
Point3D.prototype.getProjetedPoint = function(focalLength) {
var point2D = new createjs.Point();
var w = focalLength / (focalLength + this.z);
point2D.x = this.x * w;
point2D.y = this.y * w;
return point2D;
};
// Face
function Face(pos0, pos1, pos2, pos3, color) {
this.length = 4;
this.color = color;
this[0] = pos0;
this[1] = pos1;
this[2] = pos2;
this[3] = pos3;
}
Face.prototype.getFacePoints = function (points) {
var faces = this.length;
var facePoints = [];
for (var i = 0; i < faces; i++) {
facePoints[i] = points[this[i]];
}
return facePoints;
};
// MathUtils
var MathUtils = {};
MathUtils.getRandomInt = function(min, max) {
if (min > max) {
var temp = min;
min = max;
max = temp;
}
var randomNumber = Math.random() * (max - min) + min;
return Math.floor(randomNumber);
};
MathUtils.subtractVectors = function(vector0, vector1) {
var vectorX = vector1.x - vector0.x;
var vectorY = vector1.y - vector0.y;
return new createjs.Point(vectorX, vectorY);
};
MathUtils.crossProduct2D = function(vector0, vector1) {
return vector0.x * vector1.y - vector0.y * vector1.x;
}回転する立方体を描くつぎのコード2は、
var stage;
var drawGraphics;
var points;
var angle = 0;
var matrix = new createjs.Matrix2D();
var stageCenterX;
var _point = new createjs.Point();
var points2D = [];
var facesVertices;
var focalLength = 300;
function initialize() {
var canvasElement = document.getElementById("myCanvas");
stage = new createjs.Stage(canvasElement);
stageCenterX = canvasElement.width / 2;
drawGraphics = createGraphics(stageCenterX, canvasElement.height / 2);
points = createCubePoints(50);
facesVertices = getFacesVertices();
drawFaces(points, facesVertices);
createjs.Ticker.addEventListener("tick", rotate);
stage.addEventListener("stagemousemove", setAngle);
}
function setAngle(eventObject) {
var mouseX = eventObject.stageX;
angle = (mouseX - stageCenterX) * 1 / 300;
}
function rotate(eventObject) {
var count = points.length;
points2D.length = 0;
matrix.identity().rotate(angle);
for (var i = 0; i < count; i++) {
var point = points[i];
matrix.transformPoint(point.x, point.z, _point);
point.x = _point.x;
point.z = _point.y;
points2D[i] = point.getProjetedPoint(focalLength);
}
drawFaces(points2D, facesVertices);
}
function drawFaces(points, faces) {
var numFaces = faces.length;
drawGraphics.clear();
for (var i = 0; i < numFaces; i++) {
var face = faces[i];
var facePoints = face.getFacePoints(points);
if (isFront(facePoints)) {
draw(facePoints, face.color);
}
}
stage.update();
}
function isFront(facePoints) {
var origin = facePoints[0];
var point0 = MathUtils.subtractVectors(origin, facePoints[1]);
var point1 = MathUtils.subtractVectors(origin, facePoints[2]);
return (0 <= MathUtils.crossProduct2D(point0, point1));
}
function draw(points, color) {
var count = points.length;
var point = points[count - 1];
drawGraphics
.beginFill(color)
.moveTo(point.x, point.y);
for (var i = 0; i < count; i++) {
point = points[i];
drawGraphics.lineTo(point.x, point.y);
}
}
function createGraphics(x, y) {
var drawShape = new createjs.Shape();
drawShape.x = x;
drawShape.y = y;
stage.addChild(drawShape);
return drawShape.graphics;
}
function createCubePoints(halfEdge) {
var cubePoints = [
new Point3D(-halfEdge, -halfEdge, -halfEdge),
new Point3D(halfEdge, -halfEdge, -halfEdge),
new Point3D(halfEdge, halfEdge, -halfEdge),
new Point3D(-halfEdge, halfEdge, -halfEdge),
new Point3D(-halfEdge, -halfEdge, halfEdge),
new Point3D(halfEdge, -halfEdge, halfEdge),
new Point3D(halfEdge, halfEdge, halfEdge),
new Point3D(-halfEdge, halfEdge, halfEdge)
];
return cubePoints;
}
function getFacesVertices() {
var vertices = [
new Face(0, 1, 2, 3, getRandomColor()),
new Face(1, 5, 6, 2, getRandomColor()),
new Face(4, 0, 3, 7, getRandomColor()),
new Face(5, 4, 7, 6, getRandomColor())
];
return vertices;
}
function getRandomColor() {
return createjs.Graphics.getRGB(Math.floor(MathUtils.getRandomInt(0, 0xFFFFFF)));
}サンプルのコードをjsdo.
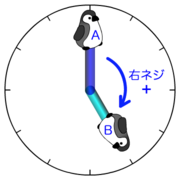
ベクトルの外積とは
ベクトルの外積についてもう少し知りたい読者のために、
| 外積の要素 | 外積のベクトルとふたつのベクトルの関係 |
|---|---|
| 角度 | ふたつのベクトルAとBを含む平面に垂直 |
| 方向 | ベクトルAからBに向かう回転を考えたとき、 |
| 大きさ | ベクトルAとBを隣り合う2辺とした平行四辺形の面積 |
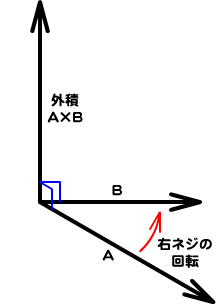
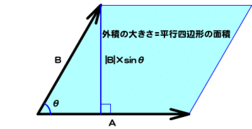
3次元空間のベクトルAとBの位置座標を、
A×B = (aybz - azby, azbx - axbz, axby - aybx)2次元平面で考えると、
A×B =axby - aybx2次元ベクトルの外積は、



