今回から3回ほどにわたって、
Box2dWebを使う
「Box2D」
まずは、
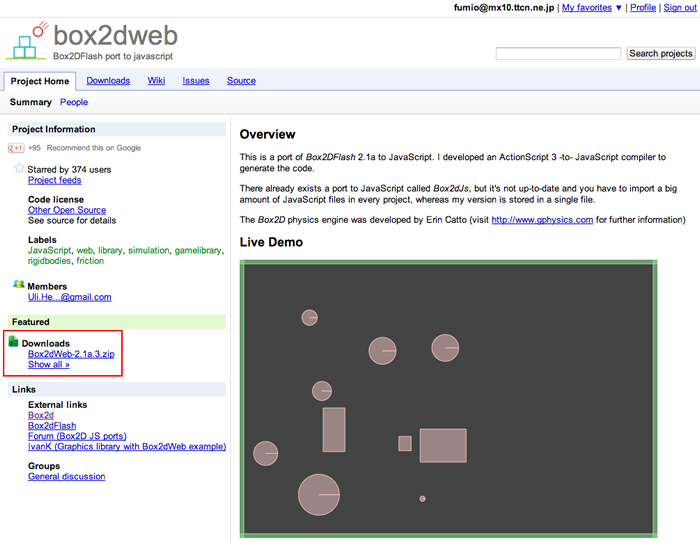
ダウンロードしたZip圧縮ファイル
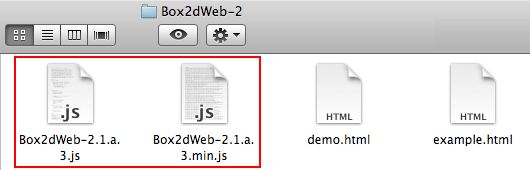
そして、
<script src="http://code.createjs.com/easeljs-0.7.1.min.js"></script>
<script src="http://code.createjs.com/preloadjs-0.4.1.min.js"></script>
<script src="lib/Box2dWeb-2.1.a.3.min.js"></script>また、
<body onLoad="initialize()">
<canvas id="myCanvas" width="400" height="300"></canvas>
</body>ボールの画像をBitmapオブジェクトに読み込む
物理演算エンジンを初めて使うとき、
先に、

Box2Dでボールをひとつ落とすスクリプトは、
画像ファイルのURLを引数に受取った関数
画像のオブジェクトをステージに置く関数
処理の行数はさほどないのに関数が多いのは、

var stage;
var ballImage;
var imageRadius;
function initialize() {
var canvasElement = document.getElementById("myCanvas");
stage = new createjs.Stage(canvasElement);
createjs.Ticker.timingMode = createjs.Ticker.RAF;
preloadImage("images/Pen.png");
}
function tick(eventObject) {
stage.update();
}
function addBall() {
var ball = createVisualBall(imageRadius);
stage.addChild(ball);
}
function createVisualBall(radius) {
var ball = new createjs.Bitmap(ballImage);
ball.regX = ballImage.width / 2;
ball.regY = ballImage.height / 2;
ball.scaleX = ball.scaleY = radius / imageRadius;
return ball;
}
function preloadImage(file) {
var loader = new createjs.LoadQueue(false);
loader.addEventListener("fileload", loadFinished);
loader.loadFile(file);
}
function loadFinished(eventObject) {
ballImage = eventObject.result;
imageRadius = ballImage.width / 2;
createjs.Ticker.addEventListener("tick", tick);
addBall();
}物理空間と剛体を定める
ここから、
- 【物理演算シミュレーションの準備】
- 物理空間をつくる
- 剛体を定義する
- 剛体定義に表示オブジェクトを関連づける
第1の物理空間は、
var world = new Box2D.Dynamics.b2World(重力, スリープ);Box2dWebには、
物理空間をつくる関数
var world;
var gravityVertical = 15;
function initialize() {
var gravity = new Box2D.Common.Math.b2Vec2(0, gravityVertical);
initializeBox2D(gravity);
}
function initializeBox2D(gravity) {
world = new Box2D.Dynamics.b2World(gravity, true);
}第2に、
| b2Body定数 | 剛体の種類 | 値 |
|---|---|---|
| b2_ | 動的 | 2 |
| b2_ | キネマティック | 1 |
| b2_ | 静的 | 0 |
剛体定義の関数
なお、
var SCALE = 1 / 30;
function addBall() {
// var ball = createVisualBall(imageRadius);
var ball = createDynamicBall(stageWidth / 2, -imageRadius, imageRadius);
}
function createDynamicBall(nX, nY, radius) {
var dynamicBody = Box2D.Dynamics.b2Body.b2_dynamicBody;
var bodyDef = defineBody(nX, nY, dynamicBody);
var ball = createVisualBall(radius, bodyDef);
return ball;
}
function defineBody(nX , nY, bodyType) {
var bodyDef = new Box2D.Dynamics.b2BodyDef();
bodyDef.position.Set(nX * SCALE, nY * SCALE);
bodyDef.type = bodyType;
return bodyDef;
}第3は、
// function createVisualBall(radius) {
function createVisualBall(radius, bodyDef) {
var ball = new createjs.Bitmap(ballImage);
bodyDef.userData = ball;
return ball;
}剛体をつくって落とす ー 物理演算シミュレーションの実行
ようやく、
- 【物理演算シミュレーションの準備】
- 剛体の定義から剛体をつくる
- 時間を進めてシミュレーションする
第4の仕事となる剛体づくりは、
b2Worldオブジェクト.CreateBody(b2BodyDefオブジェクト)b2World.
function createDynamicBall(nX, nY, radius) {
createBody(world, bodyDef);
}
function createBody(world, bodyDef) {
var body = world.CreateBody(bodyDef);
}いよいよ、
b2Worldオブジェクト.Step(経過秒数, 速度再計算, 位置再計算)人形であるボールのBitmapオブジェクトは、
物理演算の時間を進めたら、
そして、
var velocityIterations = 8;
var positionIterations = 3;
function tick(eventObject) {
var delta = eventObject.delta;
update(delta);
}
function update(delta) {
world.Step(delta / 1000, velocityIterations, positionIterations);
var body = world.GetBodyList();
var myObject = body.GetUserData();
if (myObject) {
var position = body.GetPosition();
myObject.x = position.x / SCALE;
myObject.y = position.y / SCALE;
myObject.rotation = body.GetAngle() / createjs.Matrix2D.DEG_TO_RAD;
}
}以上の5つの手順がBox2Dを使う最小限の仕込みだ。これで、

var SCALE = 1 / 30;
var stage;
var world;
var gravityVertical = 15;
var velocityIterations = 8;
var positionIterations = 3;
var stageWidth;
var stageHeight;
var ballImage;
var imageRadius;
function initialize() {
var canvasElement = document.getElementById("myCanvas");
var gravity = new Box2D.Common.Math.b2Vec2(0, gravityVertical);
stage = new createjs.Stage(canvasElement);
stageWidth = canvasElement.width;
stageHeight = canvasElement.height;
initializeBox2D(gravity);
createjs.Ticker.timingMode = createjs.Ticker.RAF;
preloadImage("images/Pen.png");
}
function initializeBox2D(gravity) {
world = new Box2D.Dynamics.b2World(gravity, true);
}
function tick(eventObject) {
var delta = eventObject.delta;
update(delta);
stage.update();
}
function addBall() {
var ball = createDynamicBall(stageWidth / 2, -imageRadius, imageRadius);
stage.addChild(ball);
}
function createDynamicBall(nX, nY, radius) {
var dynamicBody = Box2D.Dynamics.b2Body.b2_dynamicBody;
var bodyDef = defineBody(nX, nY, dynamicBody);
var ball = createVisualBall(radius, bodyDef);
createBody(world, bodyDef);
return ball;
}
function defineBody(nX , nY, bodyType) {
var bodyDef = new Box2D.Dynamics.b2BodyDef();
bodyDef.position.Set(nX * SCALE, nY * SCALE);
bodyDef.type = bodyType;
return bodyDef;
}
function createBody(world, bodyDef) {
var body = world.CreateBody(bodyDef);
}
function update(delta) {
world.Step(delta / 1000, velocityIterations, positionIterations);
var body = world.GetBodyList();
var myObject = body.GetUserData();
if (myObject) {
var position = body.GetPosition();
myObject.x = position.x / SCALE;
myObject.y = position.y / SCALE;
myObject.rotation = body.GetAngle() / createjs.Matrix2D.DEG_TO_RAD;
}
}
function createVisualBall(radius, bodyDef) {
var ball = new createjs.Bitmap(ballImage);
ball.regX = ballImage.width / 2;
ball.regY = ballImage.height / 2;
ball.scaleX = ball.scaleY = radius / imageRadius;
bodyDef.userData = ball;
return ball;
}
function preloadImage(file) {
var loader = new createjs.LoadQueue(false);
loader.addEventListener("fileload", loadFinished);
loader.loadFile(file);
}
function loadFinished(eventObject) {
ballImage = eventObject.result;
imageRadius = ballImage.width / 2;
createjs.Ticker.addEventListener("tick", tick);
addBall();
}結果がつまらないのは、



