あけましておめでとうございます。田部井と申します。技術評論社様から「機械学習最前線」というテーマで執筆依頼をいただき、初めて記事を寄稿させていただきます。

昨年, 私はNIPSという機械学習分野の最難関の国際会議に参加したのですが,そこでの発表を中心にまとめさせていただければと思います。ただし, 機械学習分野は多岐にわたりとても一人の知識でカバーできるものではありません。そこで本稿では, 近年, 注目を集めてきた離散最適化, 特に劣モジュラー関数最適化の機械学習への応用に関する発表を紹介させていただきます。

NIPSとは

NIPS（Neural Information Processing Systems）とは, 毎年カナダのバンクーバーとウィスラーで開催される機械学習分野最難関の国際会議です。例年の採択率は30％台で, 基本全員がポスター発表としてアクセプトされ、特に得点の高い論文には, 20分の口頭発表の機会があるオーラル, 4分のポスターの概要説明の機会があるスポットライトの特典が付きます。しかし, 今年の採択率は30％を下回り24％（293/1219）で, その内オーラルは6％（18/293）, スポットライトは18％（54/293）でした。参加者も1,350人と大盛況で, 休憩時間にコーヒーを取りに行くのも一苦労するぐらいでした。

昨年のNIPSでは, 劣モジュラー最適化に関する論文が目立ちました。全部で4件^[4][5][6]の発表がありましたが, その内1件が口頭発表^［4］, 2件がスポットライト発表^[5][6]でした。

劣モジュラー関数について

劣モジュラー関数とは、集合上の収穫逓減をもつ関数（小さい集合に要素を加えるほうが, 大きい集合に加えるよりも効用が大きい性質を持つ関数、図1）のことで、連続関数上の凸性と関係しています。近年, 機械学習に現れるいろいろな関数（エントロピー, 情報利得関数など）が劣モジュラー性をもつことが示され、注目を集めています。

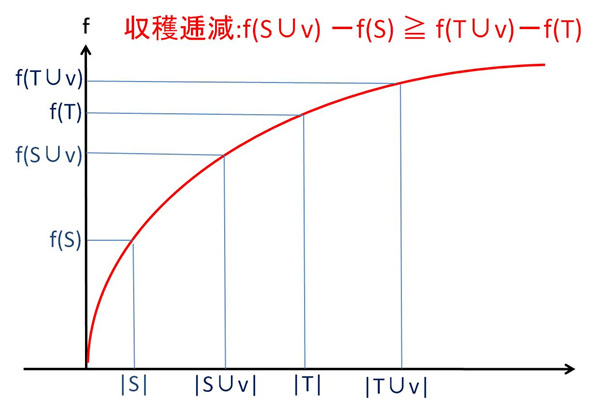
劣モジュラー関数最小化は多項式時間アルゴリズム^［1］が知られていますが, 最大化はNP困難であり近似アルゴリズムや実用的なアルゴリズム^［2］が提案されています。

また、劣モジュラー関数最適化において, 連続関数上の凸最適化との関係を示す上で重要なロヴァース拡張があります。これは劣モジュラー関数を連続関数に対応させる方法です（表1-(1)⁠）⁠。さらに, ロヴァース拡張において重要な定理は, ある集合関数が劣モジュラー関数ならばその時に限りロヴァース拡張により得られた連続関数は凸関数であることです（表1-(2)⁠）⁠。

なお、劣モジュラー性についてさらに知りたい方は、チュートリアル^［3］が参考になります。

昨年のNIPSでの動向

それでは、昨年のNIPSでの動向を見てみましょう。

Bach^［4］は、L∞ノルムが劣モジュラー関数のロヴァース拡張から導出できることを示すことにより, 劣モジュラー性とスパース性との関係を示しました。さらに, この洞察から教師あり学習で用いることができる新しい3つのノルムを提案しました。また、勾配法や近接法が劣モジュラー関数最適化に使えることを示し, 実験によりL1,とL2ノルムを用いるより精度が良いことを示しました。

Stobbe and Krause^［5］は、劣モジュラー関数を凹関数の和として分解できる新しいクラス（decomposable submodular function）を定義し, カット問題, マルコフ確率場の最適化, 集合被覆問題などがその新しいクラスの最小化問題として定式化できることを示しました。さらに, その最小化問題を勾配法にて効率的に解くアルゴリズム（Smoothed Lovasz Gradient）を提案しました。実験により, 大規模なマルコフ確率場の最適化に適応できることも示しています。

Naganoら^［6］は, Narashimhanら^［7］により定式化されたクラスタリングとクラスター数を同時に求める問題（NP-困難）を, 平均費用最小化として定式化し, 多項式時間アルゴリズムを提案しました。

その他、離散最適化に関するワークショップでもいろいろな議論がされていたようです。その離散最適化に関する発表では, Leung^［9］は大規模なパラメトリック最大流問題に対して, 実用に耐えうるオンラインアルゴリズムを提案しました。さらに, 実世界でのポートフォリオ最適化, 在庫管理, コンピュータービジョン, 物流管理などの問題がパラメトリック最大流問題に属していることを示しました。大規模な実問題を解いているという点で興味深いと思われます。

終わりに

本稿では、NIPSでの離散最適化, 特に劣モジュラー最適化に関する発表を中心に簡単にまとめました。今年開催されるICMLやNIPSなどの機械学習の国際会議では, 離散最適化に関する論文数はさらに増えると予想されます。

特に、今年流行りそうな分野は、昨年のNIPSワークショップで議論されている場合が多いです。昨年のNIPSワークショップの内容はNIPSのサイトで見ることができます。

NIPSは10年続いたカナダでの開催も昨年で終わり、今年は場所をスペインのグラナダに移し開催されるそうです。機械学習分野はどのように変化していくのか、今年1年、この分野の動向に目を離せそうもありません。

参考文献

［1］M.Queryranne: A combinatorial algorithm for minimizing symmetric submodular functions, Proceedings of the sixth annual ACM-SIAM symposium on Discrete algorithms （⁠SODA'95）.

［2］Y.Kawahara, K.Nagano, K.Tsuda, J.Bilmes: Submodularity Cuts and Applications, Proccedings of the 23rd Annual Conference on Neural Information Processings Systems （⁠NIPS'09）.

［3］F.Bach: Convex analysis and optimization with submodular functions: a tutorial. Technical report 00527714, HAL, 2010.

［4］F.Bach:Structured Sparsity-Inducing Norms Through Submodular Functions.

［5］P.Stobbe, A.Krause: Efficient Minimization of Decomposable Submodular Functions.

［6］K.Nagano, Y.Kawahara and S.Iwata: Minimum Average Cost Clustering.

［7］M.Narasimhan, N.Jojic, J.Bilmes: Q-Clustering, （⁠Proceedings of Neural Information Processing Systems）, 2005.

［8］V.Kolmogorov: Generalized roof duality and bisubmodular functions.

［9］G.Leung, N.Quadrianto, A.Smola, K.Tsioutsiouliklis: Optimal Web-Scale Tiering as a Flow Problem.