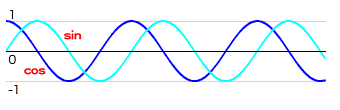
三角関数のcosとsin関数は、
バネのように振動するアニメーション - cosとsin関数
楕円軌道の前に、
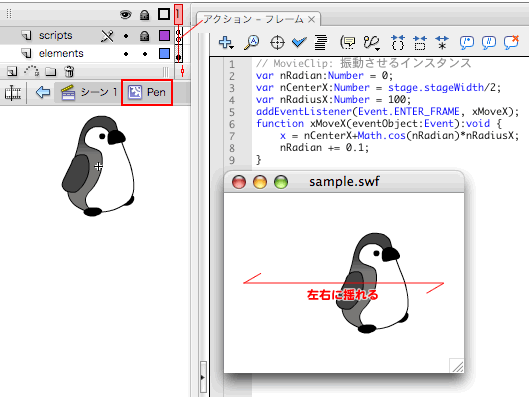
まずは、Math.で、
- 振動する水平座標=中心座標+cosθ×振幅
アニメーションさせるには、DisplayObject.イベントEvent.)
// MovieClip: 振動させるインスタンス
var nRadian:Number = 0;
var nCenterX:Number = stage.stageWidth/2;
var nRadiusX:Number = 100;
addEventListener(Event.ENTER_FRAME, xMoveX);
function xMoveX(eventObject:Event):void {
x = nCenterX+Math.cos(nRadian)*nRadiusX;
nRadian += 0.1;
}[ムービープレビュー]で確かめると、
つぎに、Math.で、
- 振動する垂直座標=中心座標+sinθ×振幅
インスタンスに記述するフレームアクションは、Math.に変えたほか、
// MovieClip: 振動させるインスタンス
var nRadian:Number = 0;
var nCenterY:Number = stage.stageHeight/2;
var nRadiusY:Number = 100;
addEventListener(Event.ENTER_FRAME, xMoveY);
function xMoveY(eventObject:Event):void {
y = nCenterY+Math.sin(nRadian)*nRadiusY;
nRadian += 0.1;
}円や楕円軌道のアニメーション
前掲スクリプト1と2を合わせて、
// MovieClip: 振動させるインスタンス
var nRadian:Number = 0;
var nCenterX:Number = stage.stageWidth/2;
var nCenterY:Number = stage.stageHeight/2;
var nRadiusX:Number = 100;
var nRadiusY:Number = 100;
addEventListener(Event.ENTER_FRAME, xMoveX);
addEventListener(Event.ENTER_FRAME, xMoveY);
addEventListener(Event.ENTER_FRAME, xUpdate);
function xMoveX(eventObject:Event):void {
x = nCenterX+Math.cos(nRadian)*nRadiusX;
}
function xMoveY(eventObject:Event):void {
y = nCenterY+Math.sin(nRadian)*nRadiusY;
}
function xUpdate(eventObject:Event):void {
nRadian += 0.1;
}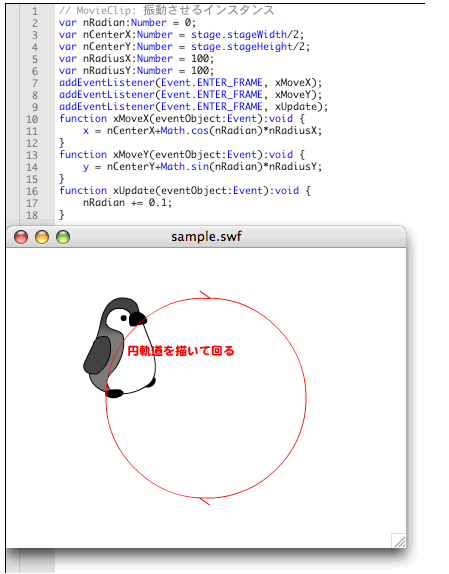
[ムービープレビュー]を見ると、
- 円軌道の水平座標=水平中心座標+cosθ×半径
- 円軌道の垂直座標=垂直中心座標+sinθ×半径
ところで、Math.やMath.メソッドに引数として渡す角度は度数ではない。変数名
- 度数=ラジアン×
(180/π) - ラジアン=度数×
(π/180)
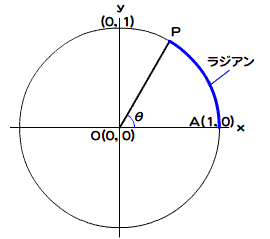
角度の変数
以下のフレームアクション
// MovieClip: 振動させるインスタンス
var nDegree:Number = 0;
var nRadian:Number = 0;
var nSpeed:Number = 5;
var nDegreeToRadian:Number = Math.PI/180;
var nCenterX:Number = stage.stageWidth/2;
var nCenterY:Number = stage.stageHeight/2;
var nRadiusX:Number = 100;
var nRadiusY:Number = 50;
var nCos:Number = Math.cos(nRadian);
var nSin:Number = Math.sin(nRadian);
addEventListener(Event.ENTER_FRAME, xMoveX);
addEventListener(Event.ENTER_FRAME, xMoveY);
addEventListener(Event.ENTER_FRAME, xUpdate);
function xMoveX(eventObject:Event):void {
x = nCenterX+nCos*nRadiusX;
}
function xMoveY(eventObject:Event):void {
y = nCenterY+nSin*nRadiusY;
}
function xUpdate(eventObject:Event):void {
nDegree += nSpeed;
nDegree = (nDegree%360+360)%360;
trace(nDegree); // 確認用
nRadian = nDegree*nDegreeToRadian;
nCos = Math.cos(nRadian);
nSin = Math.sin(nRadian);
}上記スクリプト4で説明が必要なのは、
- nDegree=(nDegree%360+360)
%360
ActionScriptのNumber型変数で扱える数値には、
%は剰余、
- nDegree=nDegree%360
しかし、
[ムービープレビュー]を確かめると、
- 楕円軌道の水平座標=水平中心座標+cosθ×水平方向の半径
- 楕円軌道の垂直座標=垂直中心座標+sinθ×垂直方向の半径
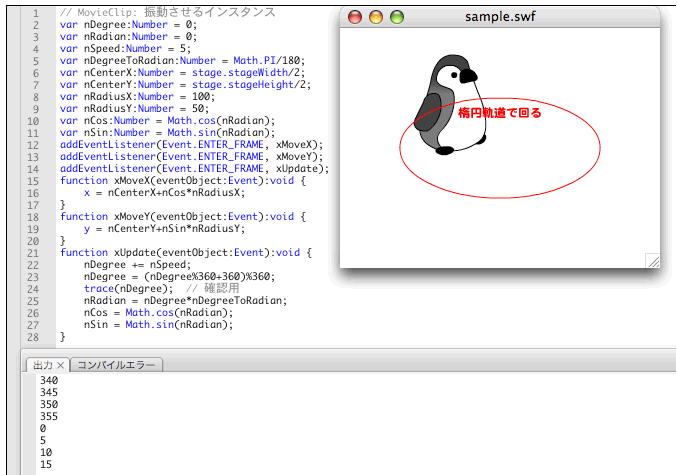
前掲スクリプト4には、
次回は、
今回解説した次のサンプルファイルがダウンロードできます。



