プログラミング言語では、論理を表現するために制御構文か論理式を使います。ところで、その制御構文や論理式は正しいのでしょうか。どうやって正しいことを確かめればよいのでしょうか。
今回は論理式の作り方と、その確認方法のひとつ、「真理値表から論理式をつくる」を紹介します。真理値表をつくることで、もれなくだぶりなく場合を尽くして状態を記述しますから、正しく論理を表現できているかどうかの確認になります。正しさを確認した表から式を立てるわけですから、少々不格好ですが、論理式の正しさ・確実さを保証することが出来ます。
たとえていえば、真理値表による論理式の作成は、マニュアルに従って作るプレハブ住宅です。決まった方法で、決まった道具を使って組み立てれば、だれでも一応住むことが出来る住宅を作れます。形は不格好でも、目的を果たすものを作ることが出来る、ということが大切です。
それでは学習を始めましょう。
図17.1 先ずは必要な要件を満たせば良し

真理値表から論理式をつくる
ある命題をプログラムに書き表したいが、その命題がいくつもの条件の絡み合ったもので、困っているとしましょう。もし、その命題を「こういうときは真、こういうときは偽」と表現できるならば真理値表を作ることができます。真理値表を作ることができれば、次に学ぶ方法で論理式をたてることができます。論理式がたてば、正しく動作するプログラムを作ることが出来ます。これは極めて機械的な作業で、小難しい理屈や計算はありません。誰にでもマスターできるシンプルな方法です。
もし、命題が十分にシンプルならば、いきなり論理式を立てることができます。例えば、「条件Aと条件Bがどちらも成り立つとき、論理値Zの値を真にする。」という命題を論理式の形にしたいとします。これは大変シンプルですから、すぐさま次の式をたてることができます。
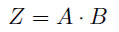
しかし、例えば「条件A、B、Cの三つのうち少なくともひとつが真の時に論理値Zを真とする。」といった場合はどうでしょう。いきなり式を立てることもできますが、その式が正しいかどうか確認する術がありません。
そんなときは、条件の取り得る状態を全て列挙し、真理値表をつくり、その真理値表を元に論理式をたてるのです。たてた式と真理値表の対応を確認することで、式の正しさを確かめることができます。
それでは具体的に手順を示します。次の命題の表す論理式を、真理値表を用いてたてましょう。
命題:「条件A、B、Cのうち、一つでも真なら論理値Zは真である。」
先ず、考えられる全ての場合を表の形にしましょう。
表17.1 全ての場合を列挙する
| A | B | C | Z |
|---|
| 0 | 0 | 0 | |
| 0 | 0 | 1 | |
| 0 | 1 | 0 | |
| 0 | 1 | 1 | |
| 1 | 0 | 0 | |
| 1 | 0 | 1 | |
| 1 | 1 | 0 | |
| 1 | 1 | 1 | |
これでA、B、Cの取り得る全ての場合を列挙しました。3桁の2進数を0から7までカウントアップしていると見なせば、もれ・ダブりのないことが確認できます。次にそれぞれの行(横の並び)のA、B、Cについて、一つでも真(1)があれば、その行のZの値に1を書き入れましょう。すると、次のようになります。
表17.2 ひとつでも真ならZ は真
| A | B | C | Z |
|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
こうして真理値表が出来上がりました。出来上がった真理値表のうち、Zが真になる場合の論理和をとります。それが求める論理式です。1行目は全て偽(0)なので除外して、その他全てが当てはまる場合です。
2行目を例にとると、Aが偽、Bも偽、Cのみが真です。このような場合を
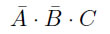
と書きます。真の場合は論理記号をそのまま書き、偽の場合は否定の記号( ̄)を付けるのです。
3行目はAが偽、Bが真、Cが偽です。この場合は
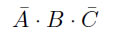
となります。以下同様に、Zが真の場合について全て書き表していき、最後に全ての場合の論理和をとります。すると次の式が出来上がります。
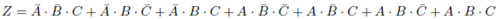
ずいぶん長い式になりましたが(※)、確かにこれが求める式です。頭の中でだけ考えていると、なかなかこの式にたどり着くことはないでしょう。
ところで、ひらめきの良い人は、条件文が次の式を表していることに気がつくかもしれません。
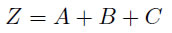
そうです。これこそ最もシンプルでエレガントな形の式です。先ほど真理値表から作った式と全く同じ意味の式なのです。びっくりするほど違いますね。命題の意味をよく考えれば、いきなりこの式をつくることもできます。ひらめきは大切ですし、すばらしいものです。しかし、だれもがいつもひらめきに満ち、経験豊かであるとは限りません。それならば、仮に出来上がった式が不格好であったり、無駄があったとしても、確実に目的通りの式が出来るのならば良いではないですか。
二つの式のうち、どちらが好ましいかと言えば、後者が圧倒的です。コンピュータに処理させるならばステップ数が劇的に違います。数多く繰り返して計算させることを考えるならば、相当速度に違いが出ます。実際に、論理を取り扱う場合には、どのエンジニアも先ず真理値表を作り、この連載でやがて学ぶ論理代数の公式や図式解法を用いてエレガントな論理式を導きます。ここで学んでいるのはその手順のスタート地点、前半戦だと言えます。
真理値表を作ってプログラムを組み立てることで、いつ、どんな場合に、どのようにプログラムを実行するのか、間違いなく書き表すことが出来ます。また、これまで、何気なく組んでいたプログラムが、たくさんのif文でこんがらがっているとしましょう。そんなとき、いったん真理値表を使って論理式をたてたうえで、if文の少ないプログラムに整理できれば、ここで学んだ甲斐があるというものです。
今回はここまで
真理値表から論理式を作る方法を紹介しました。この方法を知っていれば、少々式の形が長くなったりしますが、確実に目的通りの論理式を立てることができます。次回の演習でしっかりその練習をしてください。

![]()
![]()
![]()
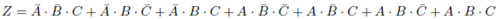
![]()
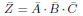 という式をたてることができます。この式を、
という式をたてることができます。この式を、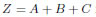 が導かれます。
が導かれます。


