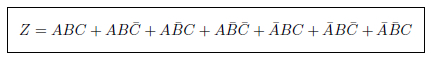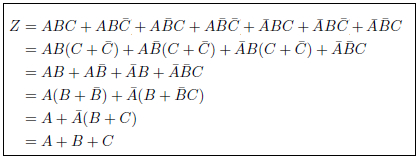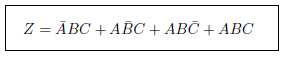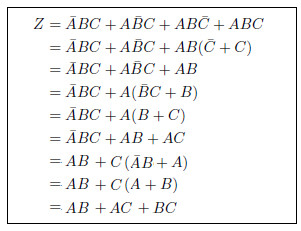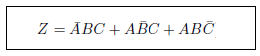前回は一通り論理代数の公式を学習し終わりました。今回はちょっと具体的に、文章の形の命題から論理式を作る練習をしましょう。今回の問題をしっかりこなした後は、皆さんが作成されたプログラムに目を移してみてください。複雑に絡み合ったif文やcase文は論理代数をつかって整理できないでしょうか。今回の学習でそういった視点を持てるだけでも意味があるというものです。
問題:命題を論理式で表現し、論理代数の公式を用いて簡略化しましょう。
(1)命題「条件A、B、Cのうち、一つでも真なら論理値Zは真である。」
これは連載第17回「真理値表から論理式をつくる 前編」の問題で紹介した命題です。真理値表から次の式を導きましたね。式の簡略化のために、積を表す”・”は省略しています。これを論理代数の公式を適用して簡略化してください。
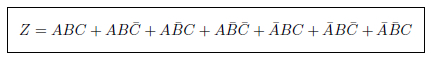
(2)命題「条件A、B、Cのうち、2つ以上真なら論理値Zは真である。」
多数決の論理式です。真理値表を作り、論理式を書き起こし、式を整理してください。
(3)命題「条件A、B、Cのうち、2つだけが真なら論理値Zは真である。」
解説
(1)命題「条件A、B、Cのうち、一つでも真なら論理値Zは真である。」
問題の式は以下のように整理できます。
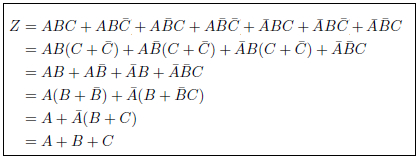
(2)命題「条件A、B、Cのうち、2つ以上真なら論理値Zは真である。」
先ずは真理値表を作ります。
表21.1 問題(2)の真理値表
| A | B | C | Z |
|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
表21.1に示す真理値表から次の式が導かれました。
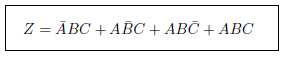
さあ、整理してみましょう。
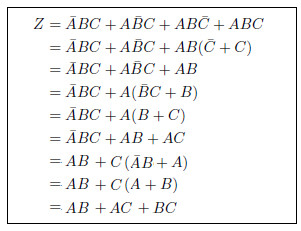
(3)命題「条件A、B、Cのうち、2つだけが真なら論理値Zは真である。」
先ずは真理値表を作ります。
表21.2 問題(3)の真理値表
| A | B | C | Z |
|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
表21.2に示す真理値表から次の式が導かれました。さあ、整理してみましょう!と意気込むのですが・・・。
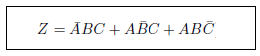
残念ですが、これはこれ以上変形できません。
お疲れ様でした
いかがですか?問題の(1)や(2)では長かった式が魔法のように短くなりましたね。シンプルな式はエレガントささえ感じさせます。カンに頼ったわけではなく、紹介した公式のみを利用してできるのです。このスキルはきっとあなたのこれからのプログラミングに役立つことでしょう。論理代数は論理回路設計では回路の単純化、消費電力低減、故障率改善のために必須の技術です。プログラミングでも同様の効果を発揮する優れた技術なのですが、意外と活用されていないし、学ばれてもいないように感じます。論理代数は、プログラミング言語がどんなに代わっても変わることのない技術です。この機会にしっかりと身につけておきましょう。