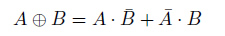前回は2変数の論理式を、カルノー図で簡略化する方法を紹介しました。今回は演習問題に取り組み、この便利な道具を自分のものにしましょう。
問題:以下に示す論理式をカルノー図を利用して式変形しましょう。
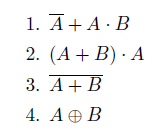
解説
1.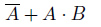
図25.1に式変形の手順を示しました。
図25.1 カルノー図で式変形1.
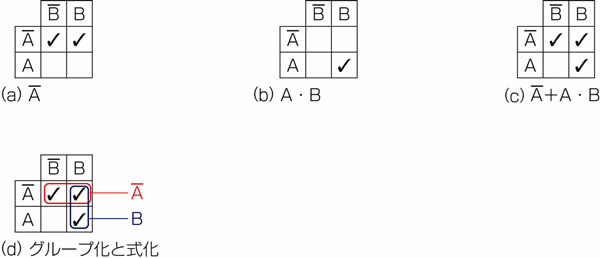
図に示す手順は、カルノー図を初めて自分で作成する、という読者を想定していますから、少々冗長で回りくどいと感じられるかもしれません。慣れたら、途中の手順を頭の中で行い、いきなり図の(c)を作成できるようになるでしょう。それでは、ステップ・バイ・ステップで解説します。
図25.1の(a)は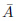 が真の場合を表す二つの枠にチェックを入れたところです。
が真の場合を表す二つの枠にチェックを入れたところです。
図25.1の(b)は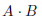 が真のところにチェックを入れたところです。一つしかありません。
が真のところにチェックを入れたところです。一つしかありません。
そして、図25.1の(c)が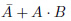 を表すカルノー図です。(a)と(b)でチェックの入ったところをあわせたものです。
を表すカルノー図です。(a)と(b)でチェックの入ったところをあわせたものです。
こうしてチェックの終わったカルノー図をぐっとにらみ、図25.1の(d)のようにグループ化します。
囲み方は長方形か正方形です。L字形はありませんから、今回はこのような赤と青、二つの囲みになります。なるべく囲みは大きく、そして囲みの数は少なくと考えれば、自然とこの形になります。
赤いグループに注目すると、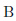 の真偽に関わらず、
の真偽に関わらず、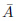 =1のときにチェックが入っています。ですから、赤いグループは
=1のときにチェックが入っています。ですから、赤いグループは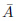 を表しています。
を表しています。
青いグループに注目すると、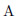 の真偽に関わらず、
の真偽に関わらず、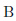 =1のときにチェックが入っています。ですから、青いグループは
=1のときにチェックが入っています。ですから、青いグループは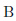 を表しています。
を表しています。
このカルノー図全体が表す論理式は、赤と青のグループの論理和です。よって、式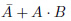 は
は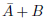 と表せることがわかりました。
と表せることがわかりました。
この結果は、連載第18回、問題の(3)で導いた結論と一致します。カルノー図が確かに有効であることがわかりますね。
2.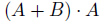
図25.2に式変形の手順を示します。
図25.2 カルノー図で式変形2.
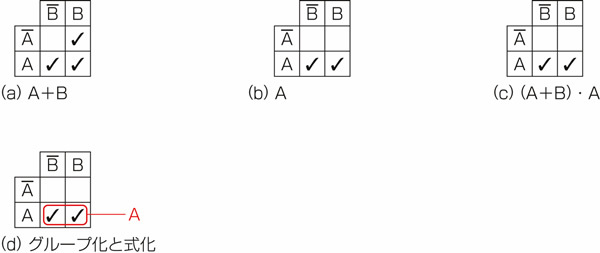
図25.2の(a)は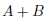 が真である枠にチェックを入れたものです。
が真である枠にチェックを入れたものです。
図25.2の(b)は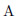 が真である枠にチェックを入れたものです。
が真である枠にチェックを入れたものです。
図25.2の(c)は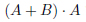 ですから、(a)と(b)で両方チェックの入っている枠を選び出したものです。
ですから、(a)と(b)で両方チェックの入っている枠を選び出したものです。
こうしてチェックの終わったカルノー図をぐっとにらみ、チェックの入った枠をできるだけ大きく、少ない数の囲みでグループ化します。すると、図25.2の(d)に示すように、赤い囲みが一つ出来上がります。この囲みは、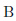 の真偽に関わらず、
の真偽に関わらず、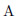 が真の時にチェックが入っています。ですから囲みが表している論理式は
が真の時にチェックが入っています。ですから囲みが表している論理式は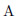 であるとわかります。従って、問題の論理式は次のように整理されます。
であるとわかります。従って、問題の論理式は次のように整理されます。
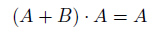
この式は連載20回『論理代数の公式[中編]』で学んだ吸収則そのものですね。
3.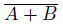
図25.3に式変形の手順を示します。式の形から、ド・モルガンの定理を取り扱おうとしていることがわかると思います。カルノー図で見事定理どおりの式が導かれるでしょうか。
図25.3 カルノー図で式変形3.

図25.3の(a)は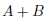 が真である枠にチェックが入っています。
が真である枠にチェックが入っています。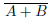 は(a)でチェックの入っていないところを表しますから、図25.3の(b)のようになります。
は(a)でチェックの入っていないところを表しますから、図25.3の(b)のようになります。
チェックの入っているところがひとつしかありませんから、図25.3の(c)のように、この枠のみが囲みの中に入ります。そしてこの囲みがあらわす論理式は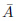 かつ
かつ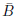 、すなわち
、すなわち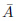 ・
・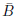 であることがわかります。
であることがわかります。
以上のことから、次のとおり、ド・モルガンの定理の式が導かれました。
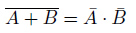
4.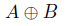
図25.4に式変形の手順を示します。排他的論理和を、カルノー図を用いて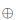 (オープラス)を用いずに表そうという試みです。
(オープラス)を用いずに表そうという試みです。
図25.4 カルノー図で式変形4.

図25.4の(a)は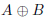 が真である枠にチェックが入っています。
が真である枠にチェックが入っています。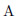 あるいは
あるいは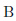 どちらかのみが真のとき、その枠が真です。
どちらかのみが真のとき、その枠が真です。
こうして出来上がったカルノー図のチェックをグループ分けしようとするのですが、それぞれチェックの入った枠の辺が接していません。図25.4の(b)のように、それぞれひとつずつの枠が個別のグループをなしています。ですから、赤い囲みと青い囲みそれぞれについて論理式を立て、それらの論理和を取ったものが全体の論理式をあらわすのです。赤の囲みは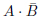 、青の囲みが
、青の囲みが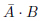 ですから、全体としては
ですから、全体としては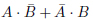 がこのカルノー図の表す論理式です。
がこのカルノー図の表す論理式です。
以上のことから、次の式が導かれます。
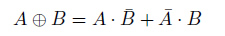
これは連載第18回『真理値表から論理式をつくる[後編]』の問題で取り組んだ、真理値表から導いた結果とも一致しています。
今回はここまで
『図による論理式の整理 その1』前編・後編では、カルノー図がいかに便利な方法か、肌で感じていただくことができたことでしょう。最もシンプルな場合として二変数のカルノー図を取り扱いましたが、実際のプログラミングでは、論理変数、すなわち命題が三つ、四つと登場します。次回はそのような論理変数が多い場合でカルノー図を利用してみます。次回紹介する内容が身につけば、多くの場合で効果を実感できるようになります。お楽しみに。
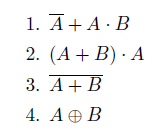
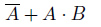

![]() が真の場合を表す二つの枠にチェックを入れたところです。
が真の場合を表す二つの枠にチェックを入れたところです。![]() が真のところにチェックを入れたところです。一つしかありません。
が真のところにチェックを入れたところです。一つしかありません。![]() を表すカルノー図です。
を表すカルノー図です。![]() の真偽に関わらず、
の真偽に関わらず、![]() =1のときにチェックが入っています。ですから、
=1のときにチェックが入っています。ですから、![]() を表しています。
を表しています。![]() の真偽に関わらず、
の真偽に関わらず、![]() =1のときにチェックが入っています。ですから、
=1のときにチェックが入っています。ですから、![]() を表しています。
を表しています。![]() は
は![]() と表せることがわかりました。
と表せることがわかりました。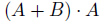

![]() が真である枠にチェックを入れたものです。
が真である枠にチェックを入れたものです。![]() が真である枠にチェックを入れたものです。
が真である枠にチェックを入れたものです。![]() ですから、
ですから、![]() の真偽に関わらず、
の真偽に関わらず、![]() が真の時にチェックが入っています。ですから囲みが表している論理式は
が真の時にチェックが入っています。ですから囲みが表している論理式は![]() であるとわかります。従って、
であるとわかります。従って、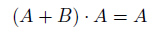
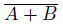

![]() が真である枠にチェックが入っています。
が真である枠にチェックが入っています。![]() は
は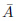 かつ
かつ![]() 、
、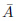 ・
・![]() であることがわかります。
であることがわかります。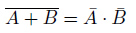
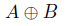
![]()

![]() が真である枠にチェックが入っています。
が真である枠にチェックが入っています。![]() あるいは
あるいは![]() どちらかのみが真のとき、
どちらかのみが真のとき、![]() 、
、![]() ですから、
ですから、![]() がこのカルノー図の表す論理式です。
がこのカルノー図の表す論理式です。