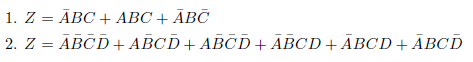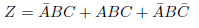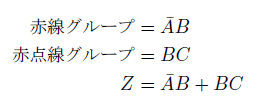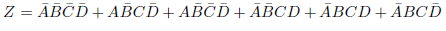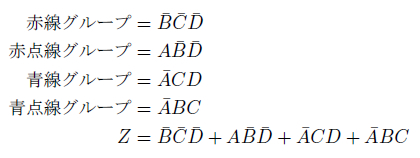今回は前回学習した3変数・4変数の場合のカルノー図を利用した演習問題をしてみましょう。カルノー図が本当に役に立つと感じられるのは，変数が3つか4つの時なのです。それより少ない場合は，論理代数で十分だと感じられますし，より多い場合はカルノー図では役不足です。今回紹介する問題で，カルノー図の真価を感じて下さい。

前回までに学んだ手順を確認しましょう。

1. カルノー図の枠を書く。
2. 与えられた論理式のそれぞれの項に対応するマスにチェックを入れる。
3. チェックをグループ化（隣り合ったチェックを四角形で囲む⁠）⁠。
4. グループ化したものを論理式にする。ひとつの囲みがひとつの項になる。
5. 全ての項の論理和をとる。以上，終わり。

ただし，以下の注意点を守ること。

1. 囲みの形はなるべく大きな長方形か正方形であること。L字形や凹凸形にならないこと。
2. 一つのグループに含まれるチェックの数は2ⁿ個であること。
3. カルノー図の左右の境界どうし，上下の境界どうしは連続しているものと考える。

それでは，どうぞ問題にチャレンジを！

問題：以下に示す論理式をカルノー図を利用して式変形しましょう。

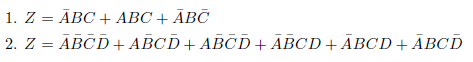
解説

1．

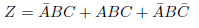
図27.1に式変形の手順を示しました。

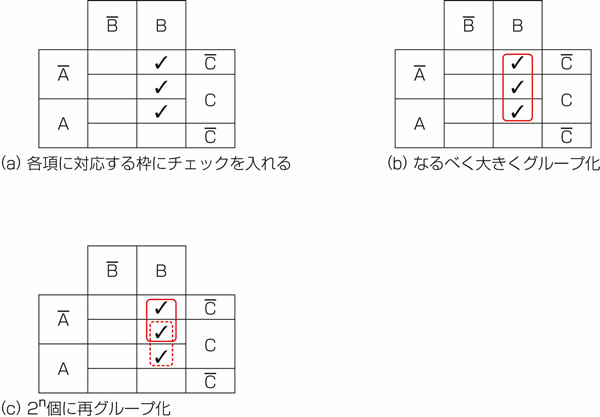
図27.1の（a）は，式の各項に対応する枠にチェックを入れたところです。この図をにらんで，できるだけ大きなグループになるように囲みます。その結果が図27.1の（b）です。囲みの中のチェックの数は3つです。これは2ⁿのルールに反しますから，切り分けを必要とします。切り分けた結果が図27.1の（c）です。さて，こうして切り分けた赤線，赤点線のグループをそれぞれ式化し，論理和をとれば求める簡略化された論理式が得られます。

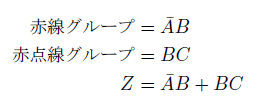
3因子3項あった論理式が，2因子2項に整理されました。

2．

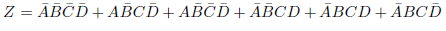
図27.2に式変形の手順を示しました。

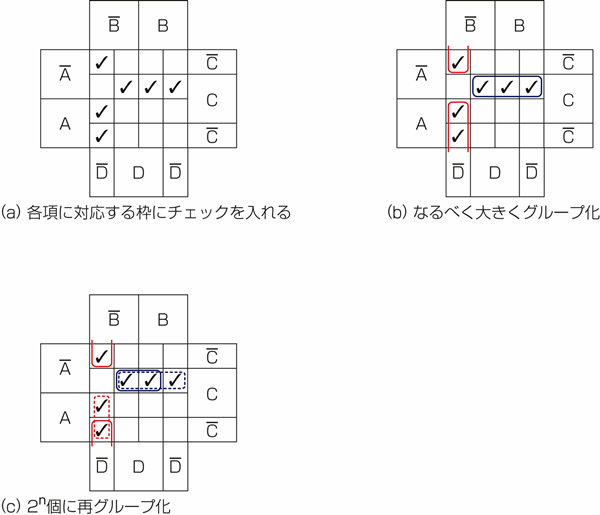
図27.2の（a）に，式の各項に対応する枠にチェックを入れたところを示しました。できるだけ大きなグループになるように囲んだ結果が図27.2の（b）です。どちらも囲みの中のチェックの数は3つです。2ⁿのルールに反しないよう切り分けた結果が図27.2の（c）です。

3変数の場合と全く手順が同じですね。

こうして切り分けたグループをそれぞれ式化し，論理和をとれば求める簡略化された論理式が得られます。

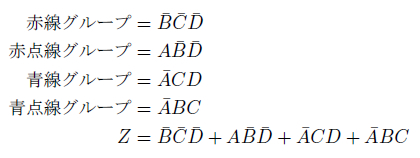
4因子6項あった論理式が3因子4項に簡略化されました。

今回はここまで

いかがでしたか？問題の論理式が，とてもシンプルな式になりましたね。論理代数の公式をひとつも使わずに！カルノー図って，本当に便利な道具です。

論理変数が4つよりも多い場合には，カルノー図はかえって不便ですので，様々な方法が開発されています（※）が，どれもちょっと簡単に，というわけにはいきません。コンピュータの数学入門者の皆さんは，先ずはここまで出来れば十分です。プログラミングの課題にカルノー図を活用してみてください。

※）

たとえば，クワイン・マクラスキー法（Quine-McCluskey algorithm）