これまで十数回にわたって論理の数学を学習しました。今回はその総まとめとして、

問題:3者の多数決をとるプログラムを作りましょう。
この課題は、
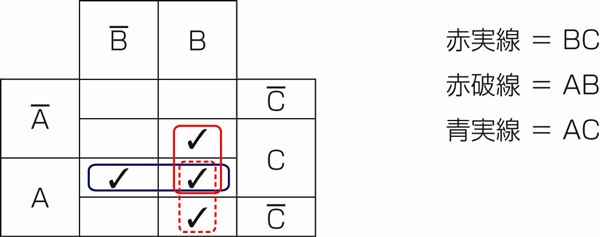
問題解決の手順を示しますのです 実行時間の計測には、 一度だけの論理式実行では大きな実行時間の差となって表れませんから、 題意の真理値表を以下に示します。Zが真をとる場合が全体の半分であることがわかります。 真理値表を元にたてた論理式を以下に示します。 取り組み カルノー図を用いて次のように簡略化てみる。 図中の各グループを論理式の各項に書き表すと次のようになります。 以上の作業により、 ついでなので、 このように、 式を整理した後の論理式は、 時間を計測するコードを加えてたものを次に示します。 お手元の環境で実行してみましょう。実行時間は使用している環境によって異なります。私の実行環境 計算処理を数万回繰り返すような場合というと、 今回取り上げた多数決の仕組みは、 論理の数学の学習は、long time = System.currentTimeMillis();解説
(1)
A B C Z F F F F F F T F F T F F F T T T T F F F T F T T T T F T T T T T (2)
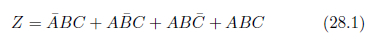
1: //filename : Tasuuketu.java
2: class Tasuuketu {
3:
4: public static void main(String[] args) {
5: boolean a,b,c,z;
6: a = true; b = false; c = false;
7: System.out.println("z("+a+","+b+","+c+") = " + z(a,b,c));
8: a = true; b = true; c = false;
9: System.out.println("z("+a+","+b+","+c+") = " + z(a,b,c));
10: }// end of main
11:
12: static boolean z(boolean a, boolean b, boolean c) {
13: return (!a&&b&&c)||(a&&!b&&c)||(a&&b&&!c)||(a&&b&&c);
14: }//end of function
15:
16: }// end of class
(4)

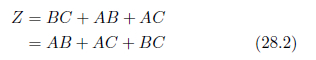
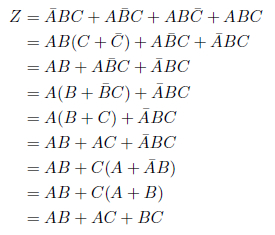
(5)
static boolean z(boolean a, boolean b, boolean c) {
return (a&&b)||(a&&c)||(b&&c);
}//end of function1: //filename : TasuuketuBench.java
2: class TasuuketuBench {
3: public static void main(String[] args) {
4: boolean a,b,c,z;
5: long time = System.currentTimeMillis();
6: System.out.println("測定開始 その1");
7: for(int i=0;i
8: a = true; b = false; c = false; z = z1(a,b,c);
9: a = true; b = true; c = false; z = z1(a,b,c);
10: }// of for i
11: time = System.currentTimeMillis() - time;
12: System.out.println("経過時刻: " + time + "[msec]");
13:
14: time = System.currentTimeMillis();
15: System.out.println("測定開始 その2");
16: for(int i=0;i
17: a = true; b = false; c = false; z = z2(a,b,c);
18: a = true; b = true; c = false; z = z2(a,b,c);
19: }// of for i
20: time = System.currentTimeMillis() - time;
21: System.out.println("経過時刻: " + time + "[msec]");
22: }// end of main
23:
24: static boolean z1(boolean a, boolean b, boolean c) {
25: return (!a&&b&&c)||(a&&!b&&c)||(a&&b&&!c)||(a&&b&&c);
26: }//end of function
27:
28: static boolean z2(boolean a, boolean b, boolean c) {
29: return (a&&b)||(a&&c)||(b&&c);
30: }//end of function
31: }// end of class
論理の数学のおわりに



