ものごとは白黒はっきりさせたいものです。なんだかぼんやりしたものを見ると、落ち着かないし、不安にさえなってしまいます。理系の人々にはそんな傾向の人が多いように感じます。逆に文系の人々は、むやみに白黒つけるのを好まないように思われます。

伝統的な講道館柔道の試合は、実は文系的です。勝敗よりも大切にするものがあるからです。もちろん、勝敗は大切なのです。しかし、最優先ではありません。一番大切なのは「良い勝負ができたか」ということです。スポーツとしての格闘技は勝つことが目的ですから、わずかでもポイントで優勢に立てば逃げることも有効な戦術です。しかし、日本柔道では尊ばれません。逃げて勝った者には、それ相応のレッテルが貼られます。このあたり、近年急速に国際化したスポーツ柔道には見られなくなってきた価値観です。日本が近代化する中で嘉納治五郎が伝えたかったのは、このことだったはずです。

数学といえば、はっきり白黒つくものの代表のように思われますが、確率の数学で取り扱うのはグレーです。結果のまだ出ていないものを予想するのが確率だからです。今回学習する確率の数学は、より現実に即した活用のための道具立てを紹介します。

確率変数

事象は式50.1で表したように、記号でまとめて表記できます。事象を記号で表したものを、確率変数[1]といいます。その事象の集合を表す場合は大文字で、個別の事象を表す場合は小文字を用います。

コインの表裏のように、裏か表かしかない場合には、確率も事象の数もはっきりします。

確率密度関数

確率変数と確率の値の関係を、次のように関数で示すことが出来ます。

各要素の現れる確率の合計は1となります。

このような関数を確率密度関数[2]といいます。

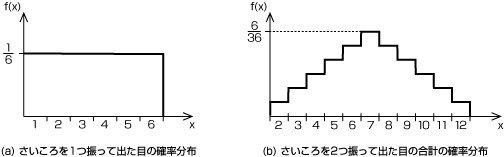
グラフの横軸に確率変数、縦軸に確率密度関数を取り、確率密度関数の曲線を描いたものを確率分布[3]といいます。さいころを１つ振って出た目の確率は均一ですから、確率分布は横一直線のグラフになります（図50.2（a）⁠）⁠。2つのさいころを振った目の合計の確率は、7になるところがピークでそれ以下、それ以上では確率が低くなることは以前に学びましたね。確率分布は山形になります（図50.2（b）⁠）⁠。

演習では、そのような確率分布を数学的に導き、またシミュレーションした結果が確かにそのようになるかどうか、つまり大数の法則に従って数学的確率と統計的確率が一致するかどうかを確認してみましょう。

問題　n個のさいころを同時に投げて、出た目の最大値をXとします。このとき、確率変数Xの確率分布を、数学的に、そして統計的に答えてください。

これは大昔にある大学の入試問題として出題されたものです。数学的確率は、紙の上で計算することで求めましょう。統計的確率は、シミュレーションするプログラムを作成して実行して求めましょう。

解説

問題：n個のさいころを同時に投げて、出た目の最大値をXとします。このとき、確率変数Xの確率分布を、数学的に、そして統計的に答えてください。

数学的に確率分布を求める

先ずは数学的に確率分布を計算してみましょう。目の最大値が1である確率とは、1の目だけが出る確率のことです。n個のさいころが全て1である確率は次の通り。

最大値が2である確率とは、n個のさいころを振って、2か1が出る確率から、1が最大値になる確率を引いたものです。すると、確率は次のように計算できます。

最大値が3である場合とは、n個のさいころを振って、3か2か1が出る場合から、2が最大値になる場合の確率を引いたものです。確率は次のように計算できます。

以下同様に考えて、全ての確率を計算することが出来ます。

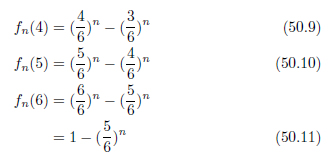
以上が正しい式ならば、全ての場合の確率を合計したものが1になるはずです。

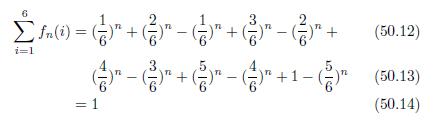
確かに1になっています。間違っていないようですね。

この確率密度関数をグラフにする、すなわち確率分布をとると、nが1のときは全て＝ですから横一直線のグラフになります。nが増加するにつれて急速に変形し、右肩上がりのシャープな分布となることが式からわかります。

統計的に確率分布を求める

実際に数学的に求めた通りになるのか、シミュレーションをして統計的に確率分布を求めてみましょう。シミュレーションに用いたコードの例を次に示します。

/*
  問題　n 個のさいころを同時に投げて、出た目の最大値をX とします。このとき、確率変数X の確率分布を、数学的に、そして統計的に答えてください。
  filename : Sample_NDiceMaxVal.java
 */

import java.util.Arrays;

class Sample_NDiceMaxVal {

  public static void main(String[] args) {

    int p = 6; //さいころの面数
     Dice d6 = new Dice(p);
    int n = 3; //さいころの個数
     int trial = 10; //試行回数
     int max[] = new int[p]; //最大値がn ならば、++new(n-1)
    int result[] = new int[n]; //複数のさいころの目を保持

    //---------------------------------
    System.out.println("6 面のダイスを" + trial + "回振り、"
             + "出た目の最大値ごとに出現回数を表示する。");

    for (int j=0; j<trial; ++j){
      for (int i=0; i<n; ++i){
        result[i] = d6.roll(1);
      }
      Arrays.sort(result); //昇順にソートされます
       ++max[result[result.length-1]-1]; //最大値の目の出現回数を++
    }
    double prob = 0;
    for (int i=0; i<p; ++i){
      System.out.print(i+1+"目"+max[i]+"回");
      prob = (Math.pow((i+1.0)/6,trial) - Math.pow((i+.0)/6,trial))*100;
      System.out.printf("P(%d) = %4.4f %% \n",i+1,prob);
    }

  }// end of main


}// end of class Sample_NDiceMaxVal

実行結果は次のようになりました。

C>java Sample_NDiceMaxVal
6 面のダイスを10 回振り、出た目の最大値ごとに出現回数を表示する。

1 目0 回P(1) = 0.0000 %
2 目0 回P(2) = 0.0017 %
3 目1 回P(3) = 0.0960 %
4 目0 回P(4) = 1.6365 %
5 目4 回P(5) = 14.4164 %
6 目5 回P(6) = 83.8494 %

試行回数を大きくすると、数学的確率は大きな目ほど更に大きくなり、100回を超えると6の目が最大である確率がほぼ100％となります。大きな目が最大値である確率が高い、ということは、題意からしても納得しやすいことでしょう。シミュレーションプログラム中の試行回数（trial）を10、100、1000と大きくして実行すると、6が最大である場合の数が、5が最大である場合の数の倍以上であることがわかります。なかなか面白い実験です。

確率密度関数のグラフは、試行回数1の時は横一直線ですが、試行回数が大きくなるに従い右にシャープなグラフになります。

今回はここまで

演習のプログラムは今回ノーヒントでしたが、無事作成できたでしょうか。解説のソースコードは、Diceクラスを利用したのでシンプルになりました。それにしても、数学的確率を計算した際はなんとなくわかったような気がする程度でした。それがシミュレーションすることで明白にドンと結果を得られました。シミュレーションとは説得力のあるものですね。