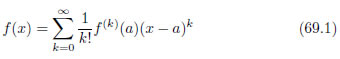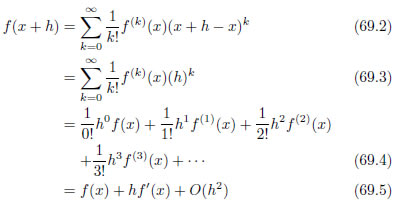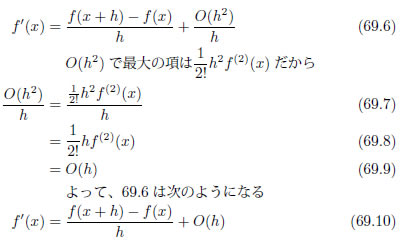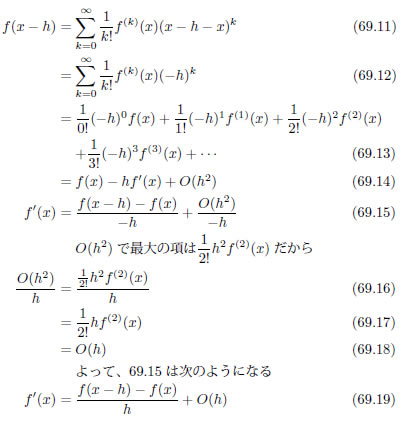料理のレシピを読んでいて困るのが「○○を少々」という表現です。量りで量れないようなわずかな分量だから「少々」と書くのです。材料が元々含む塩分や，好みによってこの「少々」が変動することはよく分かります。でも，困るのです。経験の浅い私は臆病になって「ほーんのちょっぴり」になってしまったり，加減が分からなくて「入れすぎ」になったりします。結果，妙に味のないスープになってしまったり，辛くて思わずしかめっ面したくなるような野菜炒めになってしまったり。「少々」というのは難しいものですね。「さじ加減」をしながら，だんだん上手になりたいものです。それまでは，おおよその加減で「おいしい」と思えれば，それで良しとするのが精神衛生上も良いのでしょう。

これから紹介する数値微分は，まさしくそのような手段です。「出来ないよりは，役に立つ程度に出来ればOK」そんなツールです。どうです？興味がわいたことでしょう。では，始めましょう。

数値微分とは

ニュートン・ラフソン法では関数 f（x） とその導関数 f′（x） の値を求める必要があります。関数が簡単に微分できるものならば良いのですが，複雑な関数だったり，そもそも微分が苦手な場合は，変換間違い，計算間違いをする心配があります。苦労して微分して得た導関数が間違ってたなんて，目も当てられません。

数値微分はそんな私たちの救世主です。単純な計算で微分の近似値が得られるのです。

数値微分（※1）とは，関数の描くグラフ上でとても近接した二点を結ぶ直線をとり，微分値の近似値とする方法です。

解析的に求めた微分の値と厳密には一致しませんが，目的の許容する誤差の範囲で値が得られるのならば，微分を解析的に求めることが困難な場合に助かります。数値微分の結果は，解析的に求めた微分値の検証に用いることもあります。数式の形で現象が説明出来ない場合でも，時系列で連続した測定データを得られれば，数値微分を用いて微分の近似値を得ることが出来ます。

※1）

numerical differentiation

差分近似

図69.2で紹介したのは差分近似（※2）という数値微分の方法です。なるほど，hの値が十分小さければ，おおよそ正しい微分値を得られそうです。せっかくですから，漠然とではなく，どの程度近い値が得られるものなのかを確かめます。

いま，関数 f（x） の点 x における1階微分 f′（x） の値を求めるのだとします。 h は微少な量を表すものとし， f（x+h） を点 x の周りでテイラー展開します。

テイラー展開（※3）とは，関数を多項式の形に展開する方法です。

f（x） を x = a のまわりでテイラー展開する式は次のように定義されています。

「 f（x+h） を x のまわりでテイラー展開する」ために，式69.1で， x ⇒ x+h ， a ⇒ x と読みかえます。

式69.5の O（h²） は，3項目以降の多項式の値の大きさをおおよそ示したものです。

O() （※4）は，ある式の表す数値の大きさをオーダー（桁数）で表したものです。オーダーで表示することで，基準となる数に対して，式の値がどのくらい大きいかを大雑把に示す事が出来ます。今回は基準となる数を微少な量hとし，その2乗程度の大きさがあることを表しています。

式69.5を f′（x） =の形に変形します。

こうして， f′（x） を近似する式が出来ました。式69.10を前進差分（※5）の式といいます。lim h → 0 のとき，右辺は微分の定義そのものです。数値微分では， h を適切な小さな値にして，関数の描く曲線の接線の傾きの近似値を求めるのです。 O（h） は近似によって生じた誤差で打ち切り誤差（※6）といい，今回は「たかだか h 程度」の誤差があることを表しています。

ところで， f（x+h） ではなく， f（x－h） として近似したものを後退差分（※7）といいます。これまでの解説をもとに，後退差分による f′（x） の式を導いてみてください。これを問題としましょう。

※2）

difference approximation

※3）

Taylor expansion

※4）

O表記法。Big-Oh-Notation

※5）

または前進差分商（forward difference quotient）といいます。

※6）

truncation error

※7）

backward difference

問題　後退差分による導関数の近似式を導きましょう。

前進差分による導関数の近似式導出過程を参考にして，後退差分による導関数の近似式を導出しましょう。式69.1で， x ⇒ x－h ， a ⇒ x と読みかえる他は，全く同様の操作です。

解説

問題　後退差分による導関数の近似式を導きましょう。

以下に導出の過程を示します。式の意味を確認しながら紙の上に書いていくと，すっきり納得出来るはずです。

今回はここまで

数値微分は今回解説したような式を使って計算します。しかし，前進差分，後退差分よりももう少し誤差を小さくできる「中心差分」という方法があります。また，解説の中で登場した「微少な量」は，具体的にはどのぐらい小さな量なのでしょう？ Java言語ならば，Doubleを使うでしょうから，Doubleの最小値を使えば良いのでしょうか？いえいえ，実はそんなに話は簡単ではないのです。

次回は「中心差分」と「微少な量」の決定方法について解説します。