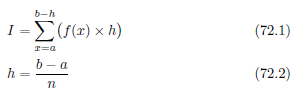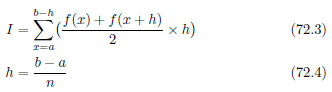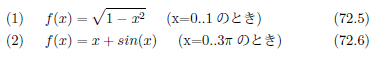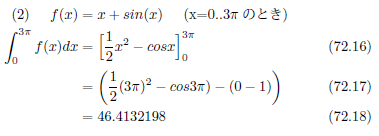火の通りにくい野菜は、二つ、三つに切ってから鍋に入れます。ゴボウなど、硬いものは細くささがけにします。キャベツも生でサラダにするときには、消化の良いように千切りに。大きいままでは食べにくい食材も、細かく切ればおいしく食べられます。
今回から学習する数値積分は、まさにそんな手段です。かなり強引な例えでしょうか?いえいえ、数々の公式やテクニックを駆使しないと積分できない関数に対面したり、大量の連続データを目の前に呆然と立ちつくしているならば、コンピュータのパワーでまさに「みじん切り」にして、お望みの結果を手に入れることが出来るのです。おいしい数値積分を、さあ、召し上がれ。
図72.1 硬い野菜は小さく切って煮込む数値積分とは
数値積分 [1] とは、積分公式を用いず、与えられた関数そのままで、関数の描く曲線で囲まれた面積の近似値を求める方法です。面積を求める、という部分に注目して、数値的求積法と呼ぶこともあります。
高校で学習する程度の微分・積分公式や計算テクニックで手計算が出来る関数であっても、積分したい範囲を様々に変更したり、関数内の定数をちょっとずつ変えて積分結果の変化を知りたい場合には、コンピュータの力を借りて数値積分するのが便利です。
数値積分は次のような状況をイメージするとわかりやすくなります。計器から時々刻々と読み取った連続データ、例えば使用電力量の総量を知りたい場合、手で計算するのは現実的ではありません。そこで、測定した値は次の測定時まで一定であると仮定しておいて、次のような計算ができます。
このような計算は、コンピュータの得意とするところです。そして、これこそ数値積分です。
今回紹介する数値積分は、冒頭の小話で書いたとおり、シンプルな方法でありながら、そこそこの精度の解が得られるうえ、人にとって苦役な計算をコンピュータにさせてしまう魅力的な方法なのです。
区分求積法
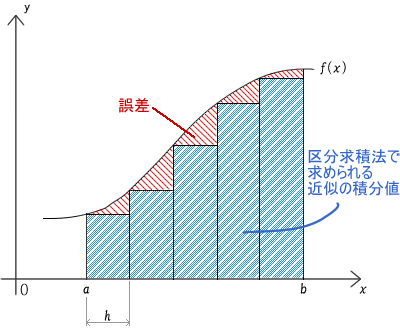
区分求積法 [2] は、最もシンプルな数値積分の方法です。図72.2 に示すように、関数 y=f(x) において、ある x のときの関数値 f(x) は、次の x+h までは一定であると仮定して、関数のグラフと x 軸に囲まれた部分の面積を求めます。シンプルだから精度が悪い、と思わないでください。場合によってはこの区分求積法が他の方法よりも精度良く計算できることがあるからです。
図72.2 区分求積法とは具体的には次のように計算します。区分点間の距離は区間 [a,b] を n 等分したものとします。
区分求積法の誤差は、面積を細切れにする幅 h を小さくすればするほど減少します。面積を細切れにするそれぞれの位置を区分点[3] といいますので、今後は h を「区分点間の距離」と呼びましょう。
では、どんどんhを小さくすれば良いかというと、弊害があります。 h を小さくすると言うことは、総和を取る回数が増え、計算時間が長くなるのです。実用的な計算時間内で結果が得られるように h を選ぶ必要があります。計算時間を短くするため、なるべく大きな h で誤差を少なくするよう工夫されたのが、次に紹介する台形公式です。
台形公式
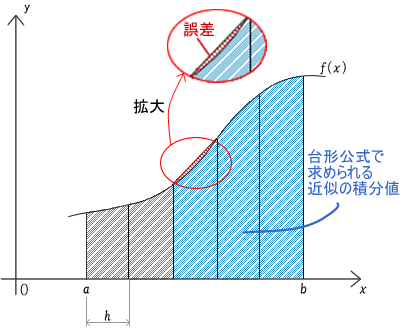
台形公式[4] は、区分求積法で発生する誤差をより小さくするために工夫された数値積分の方法です。区分点間 [a,a+h] の両端の関数値間を直線でつなげて出来た台形の面積を求めます。
図72.3 台形公式とは具体的には次のように計算します。区分点間の距離は区間 [a,b] を n 等分したものとします。
図72.3 に見られるように、区分求積法と比較して台形公式は大幅に誤差が少なくなっています。
誤差を更に少なくするために工夫されたのが、シンプソンの公式 [5] です。シンプソンの公式については、内容が少々複雑になりますので、この連載では取り上げません。しかし、計算方法そのものは大変シンプルでJava言語のプログラムにすることは難しくありません。台形公式よりも精度を2桁程度あげたい場合には採用を検討すると良いでしょう。
様々な数値積分法が考案されていますが、積分対象の関数や積分範囲によって、最も精度良い方法は違い、常に最適な方法はありません。先ずは今回学習した2つの方法をしっかり理解しておくのが良いでしょう。
問題 関数を数値積分するプログラムを作りましょう。
以下の2つの関数を、指定した範囲で数値積分しましょう。区分求積法と台形公式それぞれの場合で求めましょう。なお、数値計算をする前に、手計算で定積分し、あらかじめ結果を得ておきましょう。
プログラムでは、数値積分して得た結果と、定積分で導いた計算式をプログラムに記述して得た結果との差を表示しましょう。区分点間の距離 h は、20 から2-19 まで20通りで計算させてください。精度がどのように良くなるかが分かります。
解説
問題 関数を数値積分するプログラムを作りましょう。
手計算で積分値を求める様子を示します。
半径1の円の面積の四分の一を求める式ですね。式72.14 が得られたらほっとします。
正比例の直線にサインカーブを重ねたグラフです。このぐらいシンプルな式なら手計算で十分ですね。
長くなりましたので、区分求積法と台形公式による数値積分のソースコード紹介は次回にいたします。その際、式72.14と72.17 の式をコードに記述し、数値計算の結果と減算をした差を表示させましょう。
今回はここまで
数値積分の方法を2つ紹介しました。問題では微分や積分の公式を思い出さなければならないので、苦手な方もおられることでしょう。今回紹介した数値積分のアルゴリズムは、式72.1や72.3でご覧になったとおり大変シンプルです。それでいて、ちゃんと使える値を得ることが出来ます。こんな方法もあるのだ、と頭の隅に記憶しておけば、きっと将来役に立つことがあるでしょう。では、次回までじっくりコーディングに取り組んでおいてください。
今回のまとめ
数値積分の方法として、区分求積法、台形公式の2つを紹介しました。

![]()