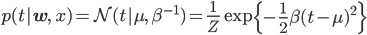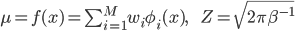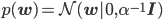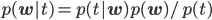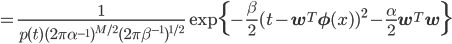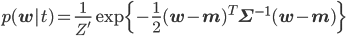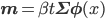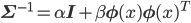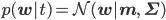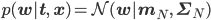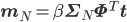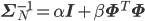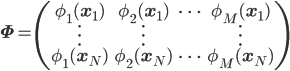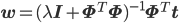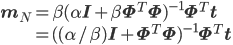さて今回は、いよいよ確率版の線形回帰をベイズ化します。
まずはベイジアンとはどういう考え方だったのか、ベイズ化するとなにが嬉しいのか、そのあたりを簡単に復習するところからはじめましょう。
ベイジアンふたたび
例えば、「コインを3回振ったら2回表が出た。だからこのコインの表の出る確率は2/3だ」と聞くとどのように感じますか?
「いや、それはたまたまでしょう」「いくらなんでも結論が早すぎる」とかいった印象を受けるのではないでしょうか。その印象の正体は、試行回数が少なすぎてコインの確率はおおむね1/2だろうという事前知識(先入観)に反する結果を信用できない、というあたりでしょう。
これがもし「コインを300回振ったら200回表が出た。だからこのコインの表の出る確率は2/3だ」だったらどうでしょう。
こちらなら「ああ、それならそうかもしれない。変なコイン……」と思えるのではないでしょうか。試行回数が増えて、事前知識に反する結果でも受け入れられるくらい信頼度が上がったわけです。
でもちょっと待ってください。この短い例題の中に、困ったことが2つもあります。
まず、その2種類の印象の違いを答えだけから知りようがありません。答えはどちらも同じ「2/3」ですからね。
そして、試行回数が3回では足りなくて、300回あれば十分、というのは主観的すぎるのではないでしょうか。答えを信用するには何回試行すればいいか、その基準があいまいです。
このような問題を解決する1つの方法が、第10回で紹介したベイジアンの考え方でした。答えを1つの値として求めるのではなく、値それぞれに対する「自信」を確率分布として求めるものでしたね。
事前分布などのこまかな話はおいておき、上の問題を試しにベイジアンのもとで解くと、「コインを3回振ったら2回表が出たとき」と「300回振ったら200回表が出たとき」の、「コインの表の出る確率」の自信(分布)はそれぞれ図の赤線と青線のようになります。
図1 赤線は左の軸に、青線は右の軸にしたがう。スケールが違うが、今は分布の形だけに注目している
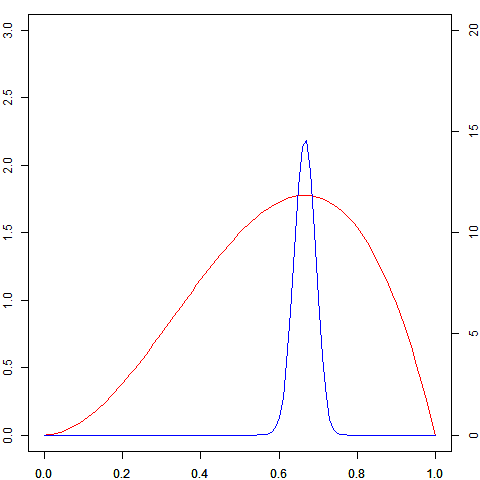
赤線の分布なら「一応2/3が一番可能性高いけど、まだまだ全然違う値である可能性も捨てきれない」ことがわかりますし、青線の分布なら「少しくらいぶれるかもしれないけど、ほぼ2/3!」ということが言えます。
答えを確率分布として得ることで、その高さや分布の広がり方(分散)からいろいろな情報を読みとることができるのがベイジアンのメリットです。
ベイジアン+線形回帰
さてベイジアンの良さはわかりましたが、それをわざわざ線形回帰に当てはめる必要があるのでしょうか。よくよく考えてみると、線形回帰にも先ほどと同じ問題点が、もっと切実な形で存在することがわかります。
線形回帰の答えは「係数wのある値」として得られます。その値だけを見ていても、どれくらい信頼できる数字なのかは同様にわかりません。しかも、「データがいくつあれば十分信頼できるか」という判断はコインの場合よりさらに難しくなります。
図2 この「答え」は信頼できるか?
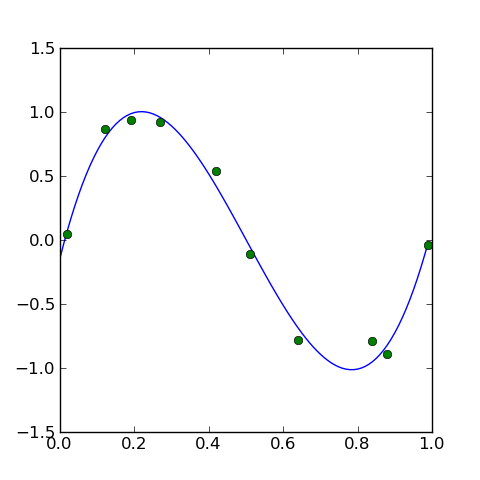
こういったグラフを描くことができれば、「だいたいOK」「いまいち」のような判断をすることもできるかもしれません。しかしやはり主観的なレベルになってしまいますし、高次元になるとそれすらかないません。
そう、だからこそ、ベイジアンの出番です。
ここまでの線形回帰では「答え」を係数wの値として求めていました。そのwを直接求めるのではなく、それぞれの値の「自信」を確率分布として求めるのがベイジアンの考え方になります。
準備として、前回までの記号を簡単にまとめます。
- (x,t):観測された値(確率変数)。入力xに対して出力tを返す関数を求める
- φi(x):基底関数(i=1,...,M)
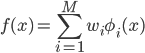 :基底関数の線形和(求める関数の候補)
:基底関数の線形和(求める関数の候補)
そして前回導入したtの条件付き分布p(t|w,x)です。線形回帰を確率化するのに必要だったこの分布が今回も活躍します。
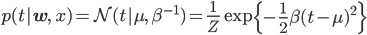 ただし
ただし 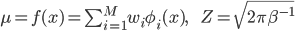
実際には複数のデータ点を扱うので、(x1,t1),...,(xN,tN)のように確率変数の列を考えるのですが、複数個の場合は後回しにして、まずはxやtは1個だけで話を進めます。特にxは入力値なので定数扱いして、p(t|w,x)もp(t|w)と記します。
さて、ベイジアンで問題を解く手順をすべて説明し直しているとさすがに話が長くなりすぎるため、要点だけなぞっていきましょう。復習したい場合は、事前分布・事後分布などについては第10回を、ベイズ公式や乗法・加法定理については第2回を参照してください。
まずは事前分布、つまりベースになるwの分布p(w)を仮定します。これについてはすぐ後で説明します。
続いて、そのp(w)とデータ点(x,t)を使って、wの分布を事後分布p(w|t)に更新します。この事後分布が求める「答えの自信」です。
事後分布への更新式はベイズ公式と乗法・加法定理から得られます。
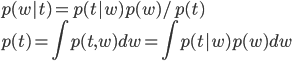
分母のp(t)は分子を積分したものになっている点にも注意してください。積分したもので割るということは、積分して1になるように調整するということですから、実はp(t)は正規化定数の役割を果たします。p(t)という書き方なのに「定数」と呼ぶのは抵抗あるかもしれませんが、wが入っていない、つまりwから見て「定数」ということですね。
このあたりはベイジアンならいつも必ず通るワンパターンな流れなので、何度か繰り返しているうちに慣れてくるかと思います。
事前分布の選び方
こうしてp(w)からp(w|t)を求められることがわかりました。そして残っているのは、肝心の事前分布p(w)をどうするかという点です。
事前分布の選び方はベイジアンにおいて非常に大きな問題の一つです。こちらもポイントだけ抜き出すと、次の2点にまとめられます。
- データ点が多ければ、事前分布に何を選んでも同じ事後分布に近づいていく
- 共役事前分布ならば計算に都合がいい
事前分布p(w)がp(t|w)と共役であれば、先の更新式に当てはめたときにp(w)とp(w|t)が同じ形の分布になります。
今回の場合の共役事前分布は正規分布になります。このことは、尤度関数p(t|w)の形から示すことができるのですが、この連載の範囲ではないため、省略しますね。
特に一番最初の事前分布として、平均が0、共分散行列が単位行列の定数倍というとても扱いやすい正規分布を選ぶことにしましょう。
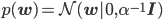
このp(w)を先ほどの更新式に代入して計算すると、以下のようになります。ただしexpの外側とp(t)は1/Z'という形にまとめてしまっています。
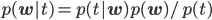
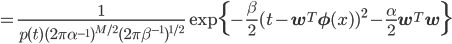
少々複雑な式が出てきてしまいました。expの中身については二次形式と呼ばれる形に頑張ってまとめて、expの前はとりあえず1/Z'と書くことにすると、以下の式に変形できることがわかっています。
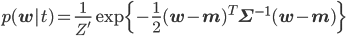 ただし
ただし
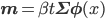
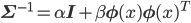
あとはZ'を求めればいい? いえいえ、実はZ'は計算する必要がないんです。
Z'にwが入っていない、つまりwから見て定数であるところがポイントです。p(w|t)はwで積分したら1になりますから、Z'はexpの部分の正規化定数に他なりません。
そのことを踏まえてexpの部分をよく見れば、それは正規分布N(w|μ,Σ)=1/Zexp(-(w-μ)TΣ-1(w-μ))のexpの部分に一致しています。つまり、p(w|t)の正体は当然そのN(w|μ,Σ)だ!、ということがZ'を求めずともわかってしまうのです。
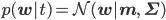
しかも、得られた事後分布も正規分布であることから、それを次のデータ点に対する「共役な」事前分布として使えます。いいことずくめ。
さて、ここまでxを固定して、つまりデータ点が1個の場合に限って話してきましたが、N個のデータ点x=(x1,……,xN)T,t=(t1,……,tN)Tに対しても、その事後分布p(w|t,x)を同じように求めることができます。詳しい計算は省略しますが、その分布もやはり以下のような正規分布となります。
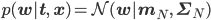 ただし
ただし
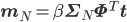
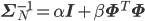
Φは第11回に登場した、次のように定義される行列です。
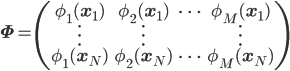
この結果は、まずデータ点(x1,t1)に対してその事後分布p(w|t1,x1)を求め、それをまた事前分布とみなし、別のデータ点(x2,t2)を使って次の事後分布p(w|t1,t2,x1,x2)を求めて……という操作を繰り返して得られるp(w|t1,……,tN,x1,……,xN)と同じ分布になります。
一見、当たり前のことを言っているだけに聞こえるかもしれませんが、結果がデータの順序によって違ってしまっては困ったことになりますので、こうした確認はとても重要です。
ベイズ線形回帰を解く
「ベイズ線形回帰を解く」と見出しを付けましたが、事後分布を求めたことで、すでにもう解けています。
wの事後分布p(w|t)=N(w|μN,ΣN)は正規分布ですから、平均のμNを頂点とするいわゆる釣り鐘型の分布になります。したがって一番「自信」のある、つまり一番確率の高い答えはw=μNです。
このように事後分布の最大点をwの推定値とみなす手法には、事後分布最大化(Maximum a Posterior、MAP)推定という名前が付いています。
「自信」の度合いは裾の広がり具合から知ることができます。それは共分散ΣNを見ればわかるのですが、読み解くのに少しコツがいります。
これは具体例で説明する方がわかりやすいので、次回の実践編の中で紹介することにしましょう。
正則化ふたたび
なんか毎回似たような小難しい式がいっぱい出てくるから、どれがどれだか……などと感じられているかもしれませんね。
例えば、第9回や第11回に出てきた正則化付きの線形回帰の結果などはかなりよく似た式のように見えます。ここでλは正則化係数という、正則化の係具合を調整するパラメータでしたね。
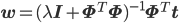
あれ? よくよく見ると、単に似ているというレベルではなさそうです。先ほどのmNの式にΣNを代入してみましょう。
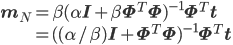
なんと、λがα/βに置き替わっているだけで、全く同じ式になっています!
ベイズ線形回帰では、p(w)は「事前分布の仮定」、p(t|w)は「モデルの仮定」からそれぞれ適切に決めました。
一方の正則化付きの線形回帰では、二乗誤差が「モデルの仮定」であり、さらに二乗の正則化項をペナルティとして加えることで過学習的振る舞いを抑えるという仮定を追加していました。
こうして言葉にすると全く異なるように思える仮定から、同じ結果が得られていたわけです。
前回のまとめでも、機械学習は「仮定」の積み重ねであることを確認し、「全く異なる仮定を入れたのに同じ結果が導かれた」ことには、それらの仮定の選び方にある種の妥当性を与えてくれるのだ、という話をしていましたね。
線形回帰のベイズ化と正則化が同じ最適解を導くことも、やはりとても意味のあることなのです。
まとめ
今回、ベイジアンのもとで線形回帰を解いてみましたが、肝心の共分散をきちんと見ていないため、まだ分布で解を求めたという実感がないかもしれません。
次回はベイズ線形回帰のコードを書いて、具体的なデータで解いてみることで、そのあたりを少しでも実感してもらおうと思います。お楽しみに。


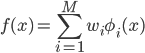 :基底関数の線形和
:基底関数の線形和