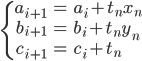前回まで扱っていた回帰問題は、データ点にマッチした関数を見つけるものでしたが、機械学習には他にも様々な問題を解くための手法があります。
今回からはその中の一つ、「分類問題」に入っていきましょう。
分類問題
「分類問題」とは、データをそれぞれカテゴリに分類するもので、機械学習の代表的な使い道の一つです。
例えばメールをスパムと非スパムに分類したり、文中の単語に名詞や動詞などの品詞ラベルを割り振ったり、Webページの内容に応じて「スポーツ」や「政治」などのジャンルに分類したりするのもすべて分類問題と見なすことで、機械学習を使って解くことができるようになります。
「分類」に雰囲気のよく似た言葉として「クラスタリング」というものもありますが、機械学習の分野ではその2つは明確に区別しています。
「分類問題」では、データをどのようなカテゴリーに分けるかは問題を解きたい人が指定します。したがって学習用のデータには正解カテゴリーがラベルとして割り振られており、それを使って「このカテゴリに属するデータはどのようなものか」を学習します。
一方の「クラスタリング」では、一般に問題を解きたい人がカテゴリを明示的に与えることはできません。できることは「2つのデータがこういう関係を満たしていれば似ているとする」といった条件と、データ全体をいくつのかたまり(クラスタ)に分割するのかを決めることだけです[1]。
本連載では「クラスタリング」は扱いませんが、こちらも機械学習の代表的な問題の一つです。k-meansやトピックモデルなど多くの手法や考え方があります。
また、分類問題はデータを2種類に分類する二値分類と、3種類以上に分類する多値分類に大きく分けられます。
多値分類は特有の難しい問題がいくつかあるため、本連載では二値分類のみを扱うことにします。
分類関数による定式化
それでは、分類問題をコンピュータが扱える形に定式化しましょう。
「データを分類する」と一言でいうと簡単そうに聞こえますが、具体的にはどうすればよいのでしょうか。
回帰問題ではデータから関数を作りましたから、未知のデータに対してもその関数値を予測することができました。同じように考えれば、データを入力したらそのカテゴリーが出力されるような関数を作ることができればよさそうです。そのような関数は「分類関数」という単純な名前が付いています。
二値分類において、例えばメールのスパム分類の場合の「スパム」と「非スパム」のように、分類関数は2種類の「値」をとりえますが、関数という以上はそれは数値である必要があります。そこで「スパム」に+1を、「非スパム」に-1を、というように適当な数値にそれぞれ割り当てます。
当然、「なんかスパムが正の値で、非スパムが負の値ってやだなあ。逆じゃあダメなの?」とか「±1じゃあなくて0と1のほうがよくない?」といった疑問がわくことでしょう。
どのクラスをどの数値に割り当てるかは便宜的なもので、必然性はありませんから、割り当てを入れ替えても全くかまいません。そうしたところで符号が反転した分類関数が求まるだけですしね。
一方、割り当てる数値は問題の解き方やモデルにあわせて都合がよいものを使います。ここではこの後紹介するモデルにとって±1が都合がよいのでそれを選んでいますが、モデルによっては1と0などを割り当てることもあります。
さて、こうしてそれぞれのデータに対して±1の値をとる関数を作ればいいというところまできました。
関数を作るということなら、これを回帰問題として解くこともできそうな気がしますが、残念ながらそう単純にはいきません。というのも、回帰によって得られる関数は当然ながら±1以外の値も取り得るからです。
それだけのことなら「近い方の値に寄せる」というシンプルな解決方法はあります。しかし、正解ラベルが+1のデータ点では関数が値-0.5をとるより値+10をとる方が分類関数としては望ましいわけですが、回帰の二乗誤差では-0.5の方が誤差が少ないということになってしまいます。これではモデルが期待通りに学習されるとは到底思えません。
つまり、分類問題のためのモデルがやはり別に必要ということがわかります。
パーセプトロン
分類問題のモデルはとてもたくさんありますが、とても簡単な手法の一つである「パーセプトロン」を手始めに紹介しましょう。
話を簡単にするため、データ点 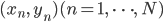 は2次元平面上にあるとします。
は2次元平面上にあるとします。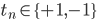 を(xn,yn)の正解ラベルとします。
を(xn,yn)の正解ラベルとします。
このとき、作りたい分類関数fは、xy平面上の点を入れると+1または-1が返ってくる関数になります。
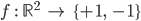
さて、前回まで紹介してきた線形回帰では、求めたい関数を基底関数の線形和の形に仮定し、そのパラメータを決定することで解くことができました。
パーセプトロンでも同じように、パラメータa、b、cを導入して、分類関数の形を次のように仮定してしまいます。
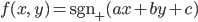
sgnは符号関数で、引数が正なら+1を、負なら-1を返します。ただしふつうの符号関数だと0に対して0が返ってきてしまって分類関数的に困るので、ここでは0のときは+1を返す変形符号関数sgn+を使うことにしましょう。
データからパラメータa、b、cを「適切に」決めることができれば、欲しい分類関数が得られます。しかし何をもって「適切」というかが次の問題になります。
線形回帰の場合は、二乗誤差が小さいことが「適切」の基準でした。したがって、二乗誤差関数が最小となるパラメータを行列の計算で求めるのでしたね。
パーセプトロンでもやはり「適切」の基準となる関数を用意します。そのためにまずあるデータ点での「誤差」を考えましょう。
単純に考えると、正解tと予測値f(x,y)の差を考えればいいような気がします。両方とも±1のどちらかしか取りませんから、差は0(正解)または2(不正解)になります。
これも立派な誤差の決め方の一つですが、パーセプトロンでは不正解のときの誤差が一律では少し困る事情があります。
詳しくはこの次項で説明しますが、ここで定義する誤差関数ができるだけ小さくなるようなパラメータは、線形回帰でやったように行列計算一発で簡単に求めることはできません。
そこで、まずはパラメータを適当に仮決めして、誤差関数がだんだん小さくなるようにパラメータを動かしていくことで、よりよい値を求めるというアプローチを取ることになります。
そのとき、正解ラベルが+1でsgn+の中身が-0.001とかの場合はパラメータを少し動かせばすぐに正の値に変わって正解になってくれそうです。一方でもし-1000とかの場合は、これを正解に持って行くにはパラメータをかなり大きく動かさなければならないでしょう。しかしどちらも誤差が同じ値であれば、パラメータをどれくらい動かせばいいのか、誤差からは推測しにくいものとなります。
そこで、正解になるまでどれくらいsgn+の中身を動かさなければならないかをパーセプトロンにおける誤差と定義します。
つまり、パラメータa、b、cの元で不正解になるデータ(xn,yn,tn)を与えるnたちをMとおくと、誤差関数は次のように表せます。
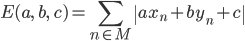 …(1)
…(1)
不正解であるということはf(xn,yn)とtnの符号が異なるということを使って、誤差関数は次のようにも表せます。ただしh(z)はz≧0のときzを、z<0のとき0をとる関数とします。
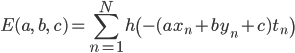 …(2)
…(2)
パーセプトロンの解き方
誤差関数が決まりましたので、あとはこれが最も小さくなるパラメータa、b、cを選べばよいだけです。どうすればできるでしょう。
線形回帰の誤差関数は、二次関数の多次元版(二次形式)という非常に扱いやすい形をしており、そのおかげで連立一次方程式を解くだけで最小点を容易に求めることができました。
一方、パーセプトロンの誤差関数はそれほど単純ではありません。
形を想像するのには(2)式の方が都合がいいのでこちらをじっとよく見ると、要はh(z)をずらしたり、のばしたり、反転したものを足しあげた形をしていることがわかります。
h(z)のグラフ
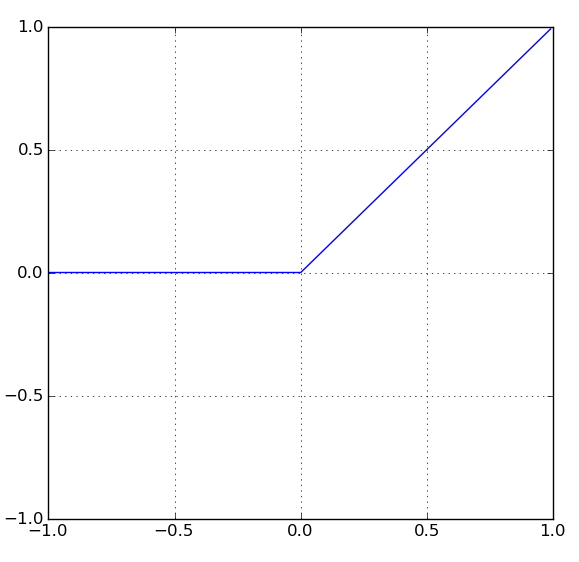
つまりパーセプトロンの誤差関数はあちらこちらでカクカクした形をしているわけです。これでは線形回帰のように簡単に最小点を求められそうにありません。
ここで、パーセプトロンの解くための実際の手順をまず見ておきましょう。このようにすれば解ける理由は次回説明します。
まず最初にパラメータa、b、cは適当に決めておきます。乱数を入れてもいいですし、(0,0,0)でもかまいません。最初に決めたパラメータをa0、b0、c0としましょう。
次に、パラメータa=ai、b=bi、c=ciを次の手順で更新していきます。
データの中からランダムに1点(xn,yn)を取り出し、f(x,y)に代入すると、現在のパラメータを用いた予測値として+1または-1が得られます。それが正解tnと一致すればOK、また別のデータを取り直します。
予測が正解と一致しなかった場合、次のようにパラメータを更新します。
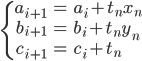
そして新たなパラメータai+1、bi+1、ci+1を使って、また別のデータ点で同じ評価を行います。これをすべてのデータ点全体についてぐるっと一周行い、もう評価していない点がなくなってしまったら、またデータ全体に対して一点ずつ同じことを繰り返します。
この操作を十分多い回数繰り返せば、f(x,y)=sgn+(ax+by+c)が分類関数として働くようなa、b、cが得られるという寸法です。
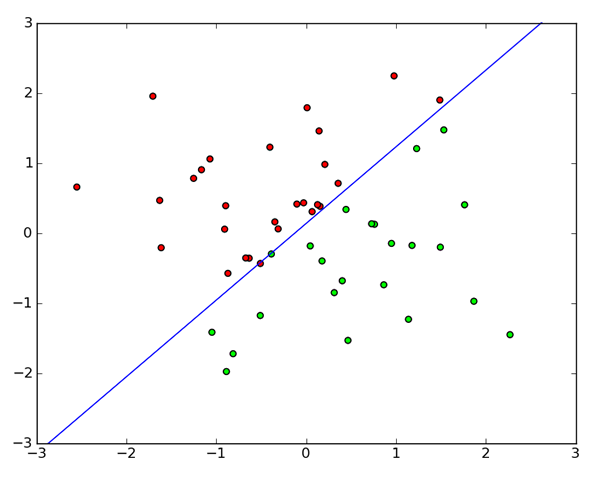
この分離関数f(x,y)が+1と-1になる領域をそれぞれ塗り分けてみると、直線ax+by+c=0によって分けられることがわかります。
実際の学習結果例は次のようになります。
赤が+1、緑が-1のデータ
このように驚くほど簡単な手順で解けてしまうパーセプトロンですが、大きな弱点があります。
パーセプトロンがきれいに解けるのは、+1のラベルを持つデータ点と-1のラベルを持つデータ点に一本の直線で(2次元の場合。n次元の場合は(n-1)次元平面で)きれいに分離できる場合にほぼ限られるのです。この条件を「線形分離可能」と呼びます。
特に線形分離可能である場合は、実は先ほどの解法手順を繰り返すことでいつか必ずすべてのデータ点での予測値が正解と一致することも示されています(パーセプトロンの収束定理)。
しかし線形分離可能ではないデータでは、どのようにパラメータを選んでもすべての予測が正解になることはありません。その場合でも「このへんだとだいたいいい感じ」という具合に切り分けてくれれば良さそうな気もしますが、評価するデータ点の順番によって全くバラバラの結果が得られてしまうのです。
試しにy=x2より上の点は+1,下の点は-1のラベルを持つデータに対して、パーセプトロンで学習した20通りの分類関数の分離面(ax+by+c=0)を描いてみたのが次の図です。このデータにパーセプトロンというのはかなり無理筋な組み合わせだとはいえ、ここまでバラバラな結果が出てきてしまうのはさすがに困ってしまいますよね。
バラバラな結果のグラフ
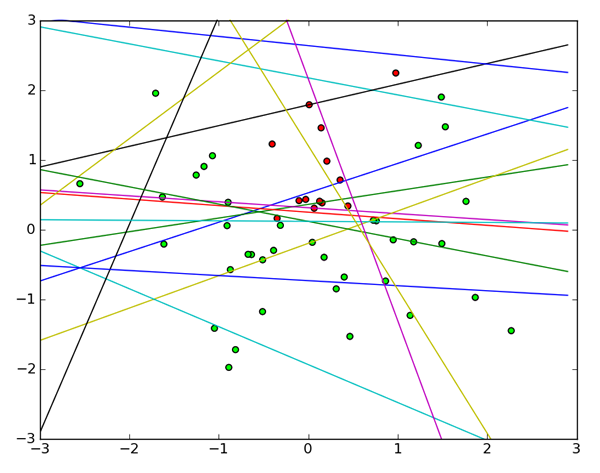
一般の問題ではデータが線形分離可能であることはまずありませんので、パーセプトロンは残念ながら実用には向いていません。
しかしながら、パーセプトロンの解法手順は、他のモデルやアルゴリズムでも使われる有用なものなのです。次回はその解説を行います。
なお本連載では取り上げませんが、パーセプトロンのこういった弱点を克服した改良型パーセプトロンもいくつかありますので、興味のある方は"Passive Aggressive"などの手法を調べてみるとよいかもしれません。
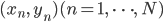 は2次元平面上にあるとします。
は2次元平面上にあるとします。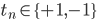 を(xn,yn)の正解ラベルとします。
を(xn,yn)の正解ラベルとします。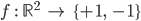
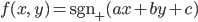
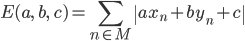 …
…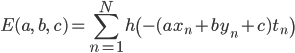 …
…