導入
コードを書いていると、
今回と次回は 構造化プログラミングで学習し身につけておきたい大事な要素、 共通点をまとめることを学習します。今回は数式の共通点をまとめることを取り扱います。
展開
数式の共通部分をまとめよう
プログラムの小さな部分といえば数式です。計算するコードを書く際は、
次の式のように共通する項が多い式は整理する価値があります。コードの見通しが良くなりますし、
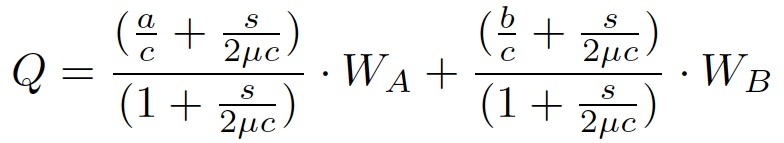
次の例ABoltPullingForceEquation.)
ABoltPullingForceEquation.pde double Q = 0;
double a = 10;
double b = 20;
double c = 30;
double s = 40;
double myu = 50;
double Wa = 60;
double Wb = 70;
// 整理しない場合
long timePassed = 0;
long timeStart = millis();
for ( long i = 0; i < 10000000; ++i ){
Q = ( a / c + s / (2 * myu * c) ) / ( 1 + s / (2 * myu * c) ) * Wa
+ ( b / c + s / (2 * myu * c) ) / ( 1 + s / (2 * myu * c) ) * Wb;
Wa += i;
Wb += i;
}
timePassed = millis() - timeStart;
println("1: Q = " + Q + ", " + timePassed + " milli sec passed.");
// 整理した場合
double term01 = 2 * myu * c;
double term02 = ( a / c + s / term01 );
double term03 = ( 1 + s / term01 );
double term04 = ( b / c + s / term01 );
Wa = 60;
Wb = 70;
timePassed = 0;
timeStart = millis();
for ( long i = 0; i < 10000000; ++i ){
Q = term02 / term03 * Wa
+ term04 / term03 * Wb;
Wa += i;
Wb += i;
}
timePassed = millis() - timeStart;
println("2: Q = " + Q + ", " + timePassed + " milli sec passed.");分解整理した後の式はコンパクトで読みやすいと感じるでしょう。計算効率も大切ですが、
[作業] sketch ABoltPullingForceEquation.中の計算式を、
公式は積極的に活用しよう
世の中には退屈な計算をだらだらと繰り返す必要のある状況があるものです。級数の公式はその代表的な例です。定義に従い、
例えば次の級数の公式を見てください。
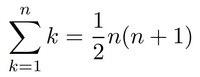
実際にこの級数を計算をするsketchを書いてみるとよくわかりますSum1ToN.)。nの値が大きくなるほど公式を使わない計算は時間がかかります。一方公式を使うとnの値がどんなに大きくても計算時間は一定かつ一瞬です。
Sum1ToN.pde //Sum1ToN.pde
double sum = 0;
double n = 100;
//定義通り計算
// sum = 1 + 2 + 3 + ... + n
//これは長いし無駄。便利なfor文を使ってみよう。
for ( int k = 1; k<=n; k++ ){
sum += k;
}
println("1: sum = " + sum);
//公式を使って計算
sum = 1. / 2 * n * ( n + 1 );
println("2: sum = " + sum);コンピュータは一定のルールに従って次々と仕事を行うことが得意ですが、
[作業] Sum1ToN.の計算をそれぞれ100万回繰り返してかかる時間を計測してみましょう。
演習
演習1(難易度:middle)
Wの値を1から100まで1ずつ変化させ、P1、P2、P3の値を求める計算を100万回繰り返しましょう。式を整理する前と後で、L=1000, l1=10, l2=20, l3=30とします。ファイル名はExercise6_としましょう。
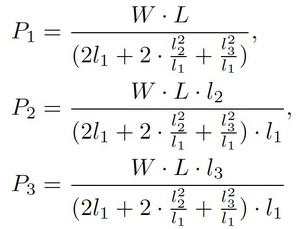
演習2(難易度:easy)
次の級数の値を求めるsketchを作成してください。a=2, r=0., n=1000として、Exercise6_としましょう。
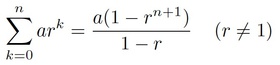
まとめ
- プログラムの最も小さな単位となる数式をまとめることを学習しました。
学習の確認
それぞれの項目で、
- 式を整理することの大切さが理解できましたか?
- 理解できた。自分のコードに活かす決心をした。
- 理解できた。しかし、
自分のコードに活かす必要を感じない。 - 理解できない。
- 公式を利用する意味を理解できましたか?
- 理解できた。
- 理解はできるが必要を感じない。
- 理解できない。
参考文献
- 『いかにして問題をとくか』
(G・ ポリア 著、 丸善株式会社) 数学的に問題を解く考え方を丁寧に解説した書籍。プログラミングは数学パズルです。是非ご一読を。
- 『ハッカーのたのしみ 本物のプログラマはいかにして問題を解くか』
(ヘンリー・ S・ ウォーレン、 ジュニア 著、 株式会社エスアイビー・ アクセス) 計算効率と速度を究極まで求めると、
こうなる。お仕事でこれを活用するのはオススメできませんが。
演習解答
- sketch
Exercise6_1. pde - 筆者の環境では式を整理した場合の方が時間がかかっていました。不思議ですが、
そういうこともあるのですね。ただし、 式の読みやすさは整理した後の方が優れています。
- 筆者の環境では式を整理した場合の方が時間がかかっていました。不思議ですが、
- sketch
Exercise6_2. pde - 圧倒的じゃないか。



