メジアンを求める　～世界の中心を目指せ～

テーブルの行に連番を振れるようになれば、SQLで自然数の特性を利用したさまざまなテクニックが使えるようになります。まずは「自然数の連続性と一意性」という特性を利用してみましょう。連続性とは「5の次が9」のような飛び石にならないということであり、一意性とは「一つの数字は一度しか現れない」ということです。

例題として、統計指標の一つであるメジアン（中央値）を求めてみましょう。メジアンとは、数値をソートして両端から数えた場合にちょうど真ん中に来る値です。単純平均と違って外れ値に影響を受けにくいという利点があります。

生徒の体重を表すテーブルがあるとします。メジアンの計算はデータ数が奇数と偶数の場合で分かれるので、サンプルテーブルも2つ用意します（表5、6⁠）⁠。奇数の場合は素直に中央の値を使えばよいのですが、偶数の場合は中央の2数の平均をとります。奇数の場合は「B343、60」の60kg、偶数の場合は「B343、60」と「B346、72」の中間の66kgが求める答えです。

集合指向的な解法

昔から知られている集合指向的な解法では、テーブルを上位集合と下位集合に分割してその共通部を取ります（リスト9⁠）⁠。この解法のポイントは、HAVING句にあります。CASE式で表現された2つの特性関数によって、母集合Weightsを上位集合と下位集合に分割しているのです（図4⁠）⁠。これはこれで「SQLらしい」解答ではあります。

SELECT AVG(weight)
  FROM (SELECT W1.weight
          FROM Weights W1, Weights W2
         GROUP BY W1.weight
               --S1（下位集合）の条件
        HAVING SUM(CASE WHEN W2.weight >= W1.weight THEN 1 ELSE 0 END)
                     >= COUNT(*) / 2
               --S2（上位集合）の条件
           AND SUM(CASE WHEN W2.weight <= W1.weight THEN 1 ELSE 0 END)
                     >= COUNT(*) / 2 ) TMP;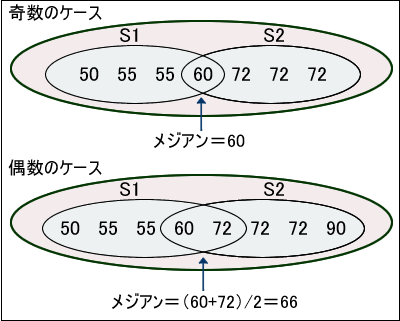

手続き型の解法

一方、自然数の特性をSQLで利用すると、まさに「端から数える」という行為をSQL上で行えるようになります。SQLに手続き型の考えを持ち込むと、リスト10のようになります。これはたとえば、世界の両端に立つ2人の旅人を想像してください。この2人が向かい合って同じ速さ（時速1レコードとしましょう）で歩いたときに、ちょうどぶつかった地点が「世界の中心」というわけです（図5⁠）⁠。

SELECT AVG(weight) AS median
  FROM (SELECT weight,
               ROW_NUMBER() OVER (ORDER BY weight ASC, student_id ASC) AS hi,
               ROW_NUMBER() OVER (ORDER BY weight DESC, student_id DESC) AS lo
         FROM Weights) TMP
  WHERE hi IN (lo, lo +1 , lo -1);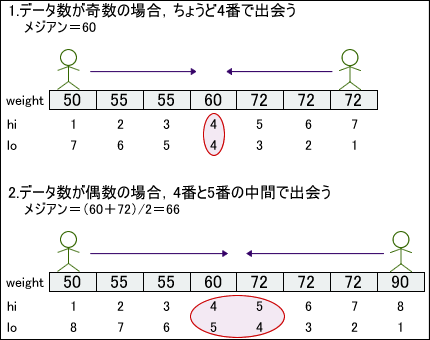

奇数の場合は、hi＝loとなる中心行が必ず1行だけ存在します。一方、偶数の場合は、hi＝lo＋1とhi＝lo－1となる2行が存在します。奇数と偶数の場合の条件分岐をIN述語でまとめてしまえる点がエレガントです。

この解法において、連番付与は必ずROW_NUMBER関数で行わなければなりません。同じOLAP関数であっても、RANKやDENSE_RANKだと「7の次が9に飛ぶ」とか「11が2つ現れる」という事態が生じてしまい、旅人の歩く速度が一定しません。行集合に自然数の集合を割りあてることで、連続性と一意性が保証されます[3]⁠。

演習問題

集合指向と手続き型、2つの異なる原理に基づくコードを比較してみると、結構おもしろいでしょう？ それでは、この問題に関して、みなさんに3つ演習問題を出しておきましょう。演習の答えはサンプルコードと一緒にダウンロードしてご覧いただけます。

問題1

リスト10の手続き的なクエリを、実装非依存で動くようROW_NUMBERを使わずに書き換えてください。

問題2

リスト10の手続き的なクエリでは、ソートキーに体重(weight) 列のほかに主キーの学生ID(student_id)を含んでいます。このキーを除外すると、このクエリは正しく動作しません。一体なぜでしょう？

問題3

問題1で使った、クラスごとに分割されたテーブル（Weights2）から、クラス単位にメジアンを求めるコードを考えます。クラス1は55kg、クラス2は72.5kg。これらを一度に求められるよう、リスト9と10の集合指向のクエリと手続き型のクエリをともに拡張してください。