入れ子集合モデルにおける更新

次に，木構造の更新を行う例として基本的な，ノードの挿入と削除を取り上げます。本当はもっと多くの処理を行う方法がありますが，紙幅の都合上，代表的なものだけを取り上げます。興味を持った方は，参考資料に挙げたテキストをご覧ください。

リーフを追加する

木にノードを追加するときは，リーフとして追加するのか，それとも親として追加するのかを決める必要があります。今回は，処理として簡単なリーフとして追加することを考えましょう。たとえば，部下を持たない猪狩氏（2,3）の配下に新たな部下，国見氏を追加することを考えます。

今，猪狩氏の直径は1しかないので，そのままだと部下を持てません。そこで，まずは猪狩氏の円を「広げる」ことを考えます。国見氏を追加するためには，猪狩氏の右端座標より右の円の座標を一律2だけ大きくすればよいことがわかります。これは，リスト6のUPDATE文で可能です。

--第一段階：追加するノードの席を空ける
UPDATE OrgChart
   SET lft = CASE WHEN lft > :parent_rgt
                  THEN lft + 2
                  ELSE lft END,
       rgt = CASE WHEN rgt >= :parent_rgt
                  THEN rgt + 2
                  ELSE rgt END
 WHERE rgt >= :parent_rgt;

--第二段階：ノードを追加する
INSERT INTO OrgChart VALUES (:child_name, :parent_rgt, (:parent_rgt + 1));

そうして猪狩氏の円の幅を広げたら，国見氏をINSERTするわけです。一般に，追加したいリーフの名前をパラメータ:child_name，親の右端座標を:parent_rgtで表せば，リーフの追加プロセスはリスト6のような二段階を踏みます。

これを今回のサンプルを使って表現すると，リスト7，図10のように具体化されます。親ノード（猪狩氏）の右端座標は3なので，:parent_rgt=3を代入します。

--第一段階：追加するノードの席を空ける
UPDATE OrgChart
   SET lft = CASE WHEN lft > 3
                  THEN lft + 2
                  ELSE lft END,
       rgt = CASE WHEN rgt >= 3
                  THEN rgt + 2
                  ELSE rgt END
 WHERE rgt >= 3;

--第二段階：国見氏を追加する
INSERT INTO OrgChart VALUES ('国見', 3, (3 + 1));

追加後の入れ子集合を図示すると，図11のようになります。猪狩氏の円が膨らんで，それに伴い，上田氏以降の円の位置が右へ2つだけずれている様子が確認できます。

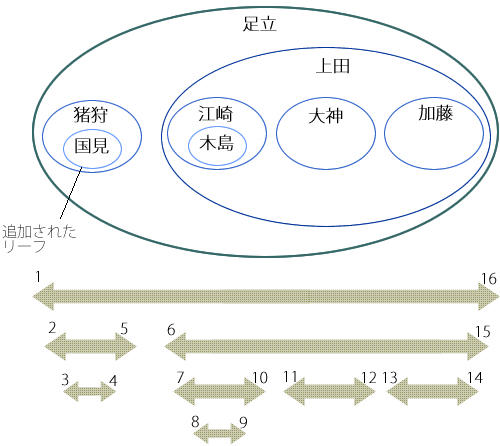
部分木の削除

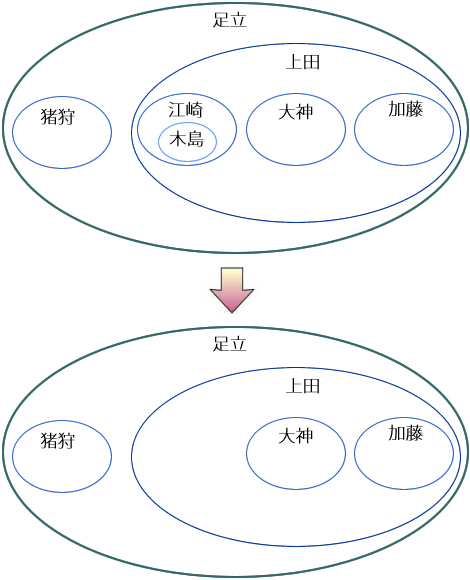
今度は逆に，木からノードを削除することを考えましょう。といっても，リーフを削除することは簡単なので，部分木の削除を例にとります。つまり，部下を持つ上司を，部下ごとクビにするのです。これは，リスト8のように解雇対象の社員の左端と右端の範囲内に含まれるノードをごっそり削除することで実現できます。:fired_empは，解雇したい社員の名前です。たとえば，江崎氏を解雇すると，連座して部下の木島氏も解雇されます（リスト9，図12・13）。

DELETE FROM OrgChart
 WHERE lft BETWEEN (SELECT lft FROM OrgChart WHERE emp = :fired_emp)
               AND (SELECT rgt FROM OrgChart WHERE emp = :fired_emp);

DELETE FROM OrgChart
 WHERE lft BETWEEN (SELECT lft FROM OrgChart WHERE emp = '江崎')
               AND (SELECT rgt FROM OrgChart WHERE emp = '江崎');

手続き型言語ならば再帰的な処理を使わねばならない木の操作も，非常に直観的に理解しやすいSQLで実現できるのが，入れ子集合モデルの大きな利点です。

おわりに

本稿で見たように，入れ子集合モデルは，RDBとSQLとのたいへん親和性の高いエレガントな方法なのですが，残念ながら欠点もあります。最大の欠点は，先にも見たように，更新時のパフォーマンスの問題です。たとえば，新しいノードを追加する場合，無関係なノードまで座標位置をずらす必要があります。木が完全な2分木で挿入位置がランダムだと仮定すると，平均で半分のノードが影響を受けます（これは順序付けられた配列に新しい要素を挿入する場合と同じです）。そのため，ノードを何百万と持つような巨大な木では，たった一つノードを追加するために，多くのノードが影響を受けることになります。もちろん，更新の間はロックもかかるため，無関係なノードへの操作も制限されてしまいます。

これを防ぐため，たとえば最初に10の倍数の座標だけを使用してあらかじめ座標の間をあけて，ノード間に「隙間」を作っておく，という逃げ手もありますが，根本的な解決策ではありません。

そこで次回では，この入れ子集合モデルの欠点を克服するための，もう一つのモデルを紹介しましょう。もう一つの，と言っても，全然無関係なものではなく，むしろ入れ子集合モデルの進化版です。実は，入れ子集合モデルはプロトタイプであり，まだ続きがあるのです。

本連載のテーマは，SQLの持つ集合論的な性格を明らかにすることでしたが，次回では，SQLが集合論と深く結びついていることを，意外な観点から確認することになるでしょう。どうぞ，お楽しみに。

参考資料

Joe Celko著『Joe Celko's Trees and Hierarchies in SQL for Smarties』

（Morgan Kaufmann Pub, 2004）

モデルの考案者自らが懇切丁寧に解説を行うのだから，入れ子集合モデルについて知りたいならば，本書1冊を読むだけで十分です。役に立つ技術書は世に多くあれど，感動する技術書はそう多くありません。しかし，残念ながら邦訳はありません。

Stephane Faroult, Peter Robson著『アート・オブ・SQL』

（オライリー・ジャパン,2007）

第7章で，階層データを扱う方法を主にパフォーマンスの観点から比較検討しています。入れ子集合モデルについては「巧妙な手法」としつつも，パフォーマンスについての欠点を指摘しています。しかし，本書はもっと本質的なことも言っていて，それは入れ子集合モデルが座標でデータを管理する以上，結局「ポインタベースの解決策」であり，RDBとSQLの理念に沿うというのは誤解だ，という批判です。これは，セルコにとってかなり痛いところを突いています。

ミック著『SQLで木と階層構造のデータを扱う（1）―入れ子集合モデル』

私が前掲の『Trees and Hierarchies』をもとに解説を行ったサイトです。検索，更新からほかの構造（隣接リストモデルやXML）から入れ子集合テーブルへの変換方法など，かなり網羅的に解説したつもりです。本稿を読んで興味を持った方は，ご覧いただければ幸いです。