はじめに
前回では、入れ子集合モデルという、リレーショナルデータベースで木構造を扱うための新しい方法論を紹介しました。このモデルは、RDB、SQLと親和性の高い優れたものではあるのですが、挿入など更新時に、無関係のノードまで変更対象としなければならないのが大きな難点でした。
そこで今回は、上記の欠点を解消する進化版のモデルを紹介します。この方法を理解していく過程で、私たちはRDBと集合論の結び付きの深さを再確認することになります。
ふだんこの連載は、1回完結の読み切り形式なのですが、今回に限り、前号の内容を前提としています。未読の方は、前号を先に読むと理解が増すでしょう。
- 稼働環境
もしも無限の資源があったなら
座標に整数のみを使う場合の限界
入れ子集合モデルの大きな欠点は、ノードを挿入(追加)するときに、自分より「右側」にある無関係なノードをもっと右へずらさなければならないことでした。前もってノード間に隙間を作って初期データを格納するという次善策もありますが、しょせんは一時しのぎです。このリソース枯渇の問題は、座標に整数を使う以上、原理的に不可避なものだからです。
そう、整数ならば、確かに、座標2と3の間にノードを追加しようと思ったとき、もう使える数はありません。手詰まりです。
有理数、実数にまで広げると
でも、もしこの小さな区間の間にも、利用できる点があったとしたらどうでしょう? たとえば、左端と右端の座標が2.3と2.7という小さな円ならば、まだ隙間に入れる余地があります(図1)。
図1 小数値の座標をとる円の挿入
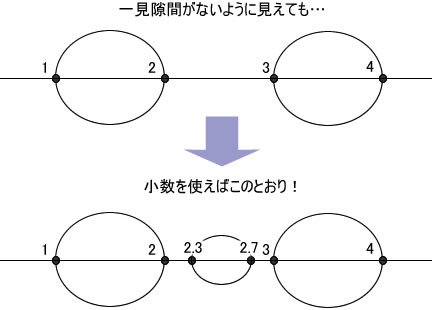
実はノードの座標が整数でなければならない理由は別にないのです。今まで整数を使っていたのは、ただ11.298とか3.777とか半端な小数よりは見た目がすっきりしていて、モデルの骨子を説明するのに便利だから、という理由に過ぎません。むしろ、有理数や実数(有理数+無理数)にまで範囲を広げたほうが、使える資源がドーンと増えて便利です。
テーブルの再作成
そうと決まれば、まずはテーブルを作り直しましょう(リスト1)。左端と右端のデータ型の定義を、次のように実数型(REAL)にします[1]。
リスト1 入れ子区間モデルによる木構造の表現
CREATE TABLE OrgChart
(emp VARCHAR(32) PRIMARY KEY,
lft REAL NOT NULL,
rgt REAL NOT NULL,
CHECK (lft < rgt));
初期データは、前回と同じく図2、3のような状態であるとします。
図2 初期データの状態
| emp(社員名) | lft(左端座標) | rgt(右端座標) |
|---|
| 足立 | 1 | 14 |
| 猪狩 | 2 | 3 |
| 上田 | 4 | 13 |
| 江崎 | 5 | 8 |
| 木島 | 6 | 7 |
| 大神 | 9 | 10 |
| 加藤 | 11 | 12 |
図3 初期データの入れ子集合による表現
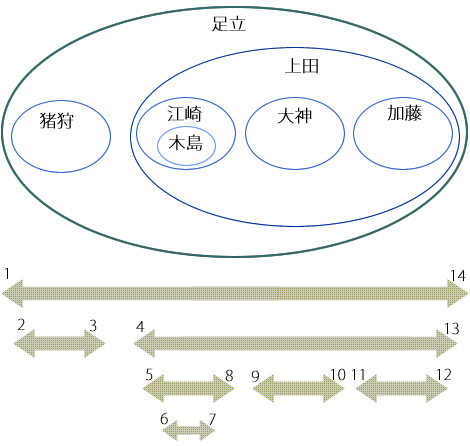
追加するノードの座標を決めるアルゴリズム
さて、次に考える必要があるのは、追加するノードの座標を決めるアルゴリズムですが、これもとくに難しくはありません。挿入対象としたい区間の左端座標をplft、右端座標をprgtとすると、次の数式によって自動的に追加ノードの座標を計算できます。
追加ノードの左端座標=(plft*2+prgt)/3 ― ⓐ追加ノードの右端座標=(plft+prgt*2)/3 ― ⓑ
なぜこれでうまくいくかというと、上記4つの座標について、必ず次の関係が成立するからです(図4)。
plft<(plft*2+prgt)/3<(plft+prgt*2)/3<prgt
図4 4点の大小関係はつねに成立する
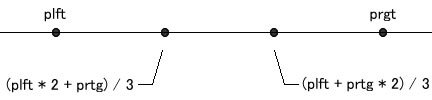
理由は、すべての辺を3倍して比較してみればわかります。
3plft<(plft*2+prgt)<(plft+prgt*2)<3prgt
今、定義によりplft<prgtです。従って、3plft<(plft*2+prgt)が成立します。あとの2辺の大小関係も同様に成立するので、区間にきちんと収まるように新しいノードを追加できることが保証されます。
データを追加してみる
座標に整数のみを利用する場合(前回の方法)
これを、前回と同じ例で考えてみましょう。前回、猪狩氏(2, 3)の下に新たに部下の国見氏を追加したとき、猪狩氏の円を広げるために、無関係な方々の円を右へずらす必要がありました(図5)。
図5 整数だと、ノード追加のために無関係のノード位置をずらさなければならない
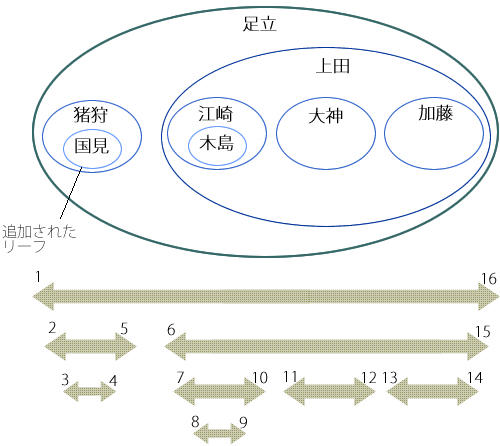
座標に有理数を利用する場合
しかし、座標に有理数を利用すれば、もうこんな大移動はする必要がありません。(2,3)の区間の中に国見氏の円を収められます(図6)。
国見氏の座標は、公式ⓐ、ⓑに従って次のように計算されます。
左端座標=(2*2+3)=2.333…右端座標=(2+3*2)=2.666…
図6 有理数なら、既存ノードへの変更なし!
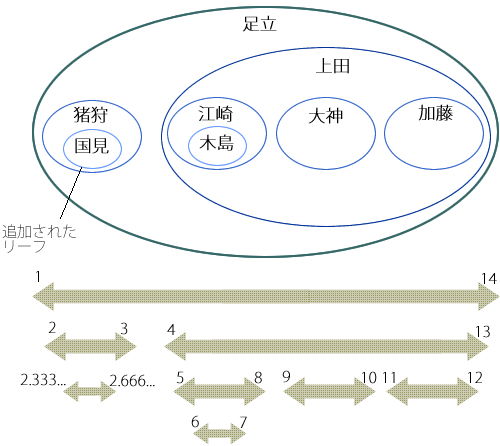
このように、座標の範囲を有理数へ広げることで、入れ子集合モデルの弱点であったノード追加時の更新処理を大きく軽減することが可能になるのです。挿入の対象とする区間は、この例のように円の「内部」でもかまいませんし、円と円の「隙間」でもかまいません。「ここに追加したい」と思う区間の左端と右端の座標を入力すれば、追加ノードの左端と右端の座標が自動的に計算されるのですから便利なものです[2]。








