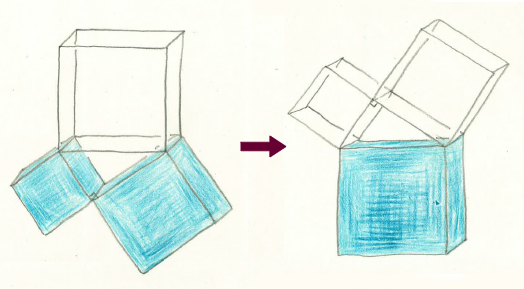
数学は抽象的な学問である。多くの定理の面白さは記号の中に凝縮されて入っていて，それを楽しみ理解するためには，一定程度の想像力を必要とする。いや，もしかしたら最大限の想像力を必要とする。しかし，いくつかの有名な定理の中には，記号ではなく具体物でその成立を実感できるものがある。それらは現実に，初等数学教育の中で教具という形で実現されているものも多い。たとえば，ピタゴラス水槽という仕掛けがある。ピタゴラスの定理（三平方の定理）の各辺上の正方形が，水槽になっていて，下側にある直角を挟む2辺上の2つの正方形の中に着色された水が入っている。それを上下入れ替えると，その水は隙間を流れて，斜辺上の大きな正方形の中にきれいに納まる。もちろん，これは証明ではない。しかしピタゴラスの定理が成り立つことが見事に実感できる。

解析学の「ホットケーキ定理」は，2次元平面上の2つの有界領域の面積を同時に2等分する一直線が存在するという定理で，中間値の定理の応用として有名である。この定理はn次元に一般化でき，証明には現代幾何学であるトポロジーが活躍するが，2次元の場合はもっと初等的な証明がある。この定理をある講座で紹介したとき，実際に目で見てこの直線の存在を確かめられる教具を作った。もちろん手作りでたいしたものではなかったが，その後，同じアイデアの教具をプロの教具作りの達人に注文した。ほどなくして，立派な教具が届いた。実際に目で見て，2つの有界領域（2つのホットケーキ）を同時に2等分する一直線（同時に2等分する切り分け方）の存在を確かめることができる。この教具を使って，ある高校で「ホットケーキ定理」の講義をしたことがある。高校生たちは見事にこの定理の核心部分を理解してくれたのだ。実感は素晴らしい。