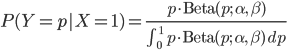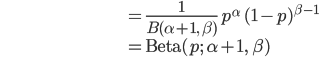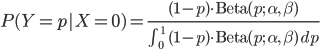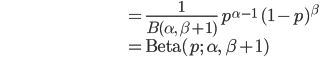これから前回の「線形回帰」を確率化した「ベイズ線形回帰」に進んでいく予定ですが、今回はその中で大活躍する「ベイズ確率」です(編注)。「ベイズ確率」は本連載の第2回で一度登場していますが、そのときは名前の紹介だけでした。
まずは「ベイズ確率」とは何で、なぜそれを使うのか、というところから見ていきましょう。
「確率」を求める
高校で確率の授業を受けたことがある人であれば、一度くらいは次のようなことを思ったことはありませんか?
「コインを投げたら表が出る確率は1/2とか、サイコロを振ったらそれぞれの目が出る確率が1/6とかよく言うけど、どうやってそれを確かめるの?」
「確率1/6といっても、6回振って各目が1回ずつ出たりしないし、仮に出たからといって、それはたまたまそうなっただけかもしれないしなあ」
具体的に、次のようなケースを考えてみましょう。
今ここに、どう見ても表が出る確率がぴったり1/2になるとは思えないほど歪んだコインがあったとします。試しにこのコインを5回投げてみたら、そのうち2回表が出ました。このときこのコインの表が出る確率は2/5と言ってもいいでしょうか。
いや、5回ではさすがに少なすぎるので、さらに20回投げたら7回表が出ました。このとき「コインの表が出る確率は (2+7) / (5+20) = 9/25 に変わった」と言えるでしょうか。コインは変わってないのに、表が出る確率が変わってもいいのでしょうか。
それとも、最初の2/5は間違いで、9/25の方が正解でしょうか。では、もう100回投げたら? 何回投げたら正解になるのでしょうか。
コインを無限回投げることができたら、正解を求めることもできるでしょう。しかし、そのようなことはできるわけありませんから、「正しい確率」を調べるのはムリ、とあきらめるしかないのでしょうか。
合格する「確率」
話は変わりますが、学生のときに試験を受けた後、友達にどれくらい自信あるかを聞かれて、「うーん、7割くらいの確率で受かってるかなあ」ということを言ったり、言われたりしたことはありませんでしたか?
そして、クラスで一番賢いヤツに聞いてみたら同じ答えだったりして、「やった! 合格率8割に上がった!! これで勝つる!!!!」とか叫んでしまったりしませんでしたか? え?下がったことならいっぱいある?
ここで言及している「確率」は、「コインの表が出る確率は1/2」=「コインを投げたら2回に1回の割合で表が出る」という「高校数学の確率」とは明らかに異なっています。
「合格率7割」とは、「試験を10回受けたら7回合格する」わけではありません。「今回の試験の結果について、7割くらいの確実さで合格が期待できると思っている」という自信のほどを表しているわけです。その時の「7割」や「8割」という数字は、経験などから導いた主観的な予測であり、数字に厳密な根拠はありません。
「確率」という言葉をそんないい加減に使っちゃあダメだ!! ……と言う人も中にはいます。第一、合否なんて試験が終了した時点ですでに決まっていて、単にまだ採点と発表を待っているだけなのだから、その結果に確率があるなんておかしいだろう、ましてや「できるヤツと答えが一緒だった(違ってた)」という理由で確率が変わるなんてありえない、とか言われたらちょっと納得しそうになります。
でもそういう細かいところは目をつむって、さきほどの「歪んだコインの確率」に今の話をあてはめてみると、おもしろい展開が待っています。
「歪んだコインの確率」は決まっているけれど、まだ知らない(合否の結果と同じく)。5回投げてみたら2回表が出た。「確率2/5」のようだ。7割くらいの自信。追加で20回投げたら7回表が出た。「確率2/5」の自信は4割くらいに下がって、「確率9/25」の自信が5割くらいに上がるかな(できるヤツの答えを聞いた時と同じく)。(注1)
この考え方なら、「コインの確率が変わるのは変」「何回投げればいいのか」という先ほどの問題が解決できます。変わるのはコインの確率ではなく「確率は2/5だろうという自信」の方であり、また新しい情報を得ることによってそれが変わるのはとても自然なことのように思えます。
しかしさすがに今のままでは、数字に根拠が無さ過ぎます。どうすれば「自信の確率」をきちんと計算することができるでしょうか。
ベイズ確率、ふたたび
実はこの「自信の確率」は、連載の第2回で「信念の度合い」と呼んでいた「ベイズ確率」と同じものなのです。
「確率のルール」を使って「自信(信念)」を形式的に計算してみたら、なかなかうまくいくことをベイズさんが発見しました。とはいえ、いわゆる「高校の確率」とはやはり明らかに異なりますから、それを「ベイズ確率」と呼ぶことにしたわけです。
確率のルールを忘れている人のために、確率のルールを再掲しておきます。見ても思い出せなかったり、事後分布ってなに?という人は、本連載の第2回や第4回で復習してくださいね。
- 離散確率:
- 確率の値は0以上1以下
- すべての取り得る値の確率の合計は1
- 連続確率:
- 確率密度関数 f(x) の値は常に0以上
- 「取り得る値の全範囲」にわたって、関数 f(x) を積分すると1になる。つまり p(全範囲)=1 となる
- 確率の加法定理
2個の確率変数 X, Y について、その同時確率 p(X,Y) と周辺確率 p(X) の間に次の等式が成り立つ。
p(Y) が離散確率の場合:
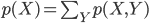
p(Y) が連続確率の場合:
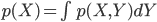
- 確率の乗法定理
2個の確率変数 X, Y について、その同時確率 p(X,Y)、条件付き確率 p(Y|X)、周辺確率 p(X) の間に次の等式が成り立つ。
p(X, Y) = p(Y|X) p(X)
確率のルールはたったこれだけ。改めて見直してみても、とても少ないですね。
事後分布 ― 結果を使って「自信」を更新
それではこの確率のルールを守って、「コインの確率の自信」を計算するとどうなるのか、実際に確かめてみましょう。
と言っても意外と簡単。X を「コインを投げたら表(X=1)が出るか裏(X=0)が出るかを表す確率変数」、Y を「コインの表が出る確率が Y(0≦Y≦1) である確率変数」と宣言して、上の確率のルールを順に当てはめて行くと、「新しい情報で『自信』がどう変わるか」の式が出てくるのです。
なお、この Y が「ベイズ確率」なのですが、「確率の確率(変数)」というややこしいものなので、混乱してしまう人もいるでしょう。
そこで、今回は特別に P(Y) を「コインの表が出る確率が Y である『自信』」と呼ぶことにしましょう。以降、「自信」と記述しているところは、本当は「(ベイズ)確率」であると考えてください。
それでは実際に計算してみましょう。まずは条件付き分布 P(X|Y) を求めます。P(X=1|Y=p) は「表が出る確率が Y=p であるコインを投げたときの、表(X=1)が出る確率」だから p です。単純ですね。
このとき、裏(X=0)の確率は 1-p ですから、次のようになります。
P(X=1|Y=p) = p
P(X=0|Y=p) = 1-p
乗法定理を使うと同時分布 P(X,Y) に直せます。P(Y) はまだわからないので、そのまま残しておきます。
P(X=1, Y=p) = P(X=1|Y=p)P(Y=p) = p P(Y=p)
P(X=0, Y=p) = P(X=0|Y=p)P(Y=p) = (1-p) P(Y=p)
一方、乗法定理を X について使うと、同時分布 P(X,Y) の別の分解が得られます。
P(X=1, Y=p) = P(Y=p|X=1)P(X=1)
P(X=0, Y=p) = P(Y=p|X=0)P(X=0)
上の2組の式を比べると、事後分布 P(Y|X) を表す次の式が得られます。これをベイズの公式というのでしたね。
P(Y=p|X=1) = p P(Y=p)/P(X=1)
P(Y=p|X=0) = (1-p)P(Y=p)/P(X=0)
分母の P(X) は加法定理を使って同時分布 P(X,Y) から Y を消すことで得られます。こちらは周辺分布というのでした。
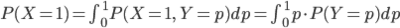
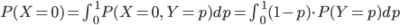
これらをあわせて、事後分布は次のようになります。
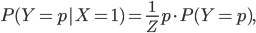 ただし
ただし 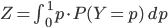
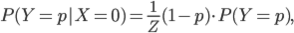 ただし
ただし 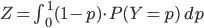
この式は、事後分布 P(Y|X) を分布 P(Y) から求められることを表しています。つまり、コインを投げて表が出た(X=1)ときの事後分布 P(Y|X=1) が、新しい「コインの表が出る確率が Y である『自信』」として採用されます。裏が出た(X=0)ときは P(Y|X=0) が選ばれます。
これが確率のルールを使った「自信」の更新です。主観や経験による漠然とした更新との最大の違いは、「誰がやっても同じ結果になる」点です。
得られた事後分布を「現在の新しい自信」とすれば、次にコインを投げた結果についても同じ操作を繰り返すことでどんどん更新された「自信」が得られます。つまり、一番最初の P(Y) さえあれば、後は何回投げても芋づる式にすべて決まります。
では、その「一番最初の自信」 P(Y) はどのように求めましょう。同じように確率のルールを使えばうまくいくのでしょうか。
事前分布 ― 最初の「自信」
実は、確率のルールをどうひねっても P(Y) を決めることはできません。つまり、一番最初の P(Y) だけは別途用意してあげる必要があります。この P(Y) を「事前分布」と呼びます。
繰り返しになりますが、確率のルールからは P(Y) には何の制約もありません。要するに、確率分布でさえあれば「なんでもいい」ということです。しかし、「なんでもいい」と言われると逆に困ってしまいますよね。「こういう事前分布がいいよ」と言ってくれる方が嬉しいものです。
そこで、「どんな事前分布だとダメなのか」を考えてみることにしましょう。試しに P(Y) を図1-aのような「ぐにゃぐにゃな分布」にしてみます。「なんでもいい」ならこんなデタラメな分布でもいいはずですが、さすがに困ったことになるのではないでしょうか。
図1
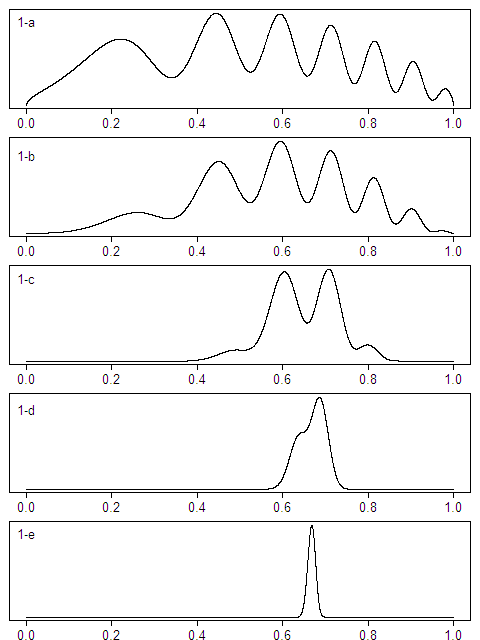
設定としては、「表が出る確率が2/3のコイン」を使います。ただし、その真の確率は知らないふりをします。そして、そのコインを投げた結果をもとに事後分布を計算すると、どういうことが起こるのかを観察するわけです。
まず「3回投げたら2回表」が出た場合の事後分布をグラフにしたのが図1-bです。ちなみに、3回投げて2回表が出るときの順番は「表表裏」「表裏表」「裏表表」の3通りありますが、順番によらず同じ事後分布になります。
グラフのぐにゃぐにゃ度は少し減っています。特に両端はほぼつぶれてます。3回投げて2回表&1回裏が出たことで、確率 0.0 や 1.0 に近いところはまずないな、という自信が出てきたという感じが出ていますね。
さらに同様に、「30回投げたら20回表」「300回投げたら200回表」「3000回投げたら2000回表」が出た場合の事後分布のグラフが図1-c, d, eです。
回数が増えるにつれて、ぐにゃぐにゃ度がどんどん下がっていき、3000回ではとうとう2/3のところに鋭い山が一つあるだけの分布になりました。そう言えば、これがコインの真の確率でしたね。
実は、最初にどのような事前分布を持ってきても、試行の回数が十分多ければ、ベイズ事後確率の一番高い値は単純な「表の回数/投げた回数」に近づくことがわかっています。つまり、どんなにデタラメに事前分布を選んでも、回数さえ多ければ結果への影響はとても小さいということです[2]。
共役事前分布 ― 都合のいい事前分布
でたらめな事前分布でも、試行の回数さえ多ければあまり困らないことは見て取れましたが、一方で回数が少なければ事前分布の影響が強く出てしまうことは図1-bや図1-cを見ればわかります。
しかし相変わらず事前分布をどうすればいいかわかりません……いや、この状況を良い方向で考えてみましょう。「計算に都合のいい、クセの少ない分布」なら事前分布に向いている、と考えるのです。
そこで、もう一度事後分布の式を眺めてみましょう。
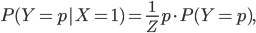 ただし
ただし 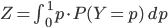
この式の中に積分が出てきていることに注目してください。一般に積分の計算はとても難しいです。「機械学習は積分との戦い」と言い切ってもいいくらい、積分をうまく計算する(あるいはうまく避ける)ことがポイントになります。
つまり、「積分をわざわざ計算しなくていい、クセの強くない分布」が「理想的な事前分布」なのですが、そんな都合のいい分布があるでしょうか。
コイン投げの場合は、「ベータ分布」という事前分布にピッタリの便利な分布があります。
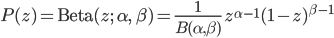 ただし
ただし 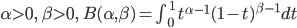
B(α,β) は「ベータ関数」と言います。
では実際に 事前分布にベータ分布 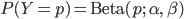 を採用して、コインの表(X=1)が出た場合の事後分布を計算してみましょう。
を採用して、コインの表(X=1)が出た場合の事後分布を計算してみましょう。
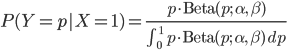
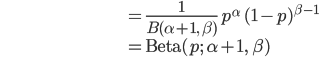
つまり、表が出た場合の事後分布は同じくベータ分布で、ただしパラメータαが1増えたものになるわけです。
裏(X=0)が出た場合の事後分布も同様に計算します。
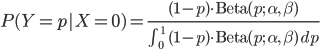
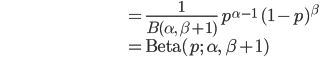
こちらもやはりベータ分布で、パラメータβが1増えたものになっていますね。
しかも事後分布が同じくベータ分布ですから、またこれを「現在の事前分布」として使うことで、次の事後分布も同様にベータ分布、その次も次も……となって、最終的に得られる事後分布は「パラメータαに表の出た回数、βに裏の出た回数を足したベータ分布」になるだろうということが少し考えてみればわかります。
つまり、コイン投げの事前分布にベータ分布を選べば、積分しなくていいどころか、計算らしい計算をしないでも事後分布がわかってしまうわけです。「機械学習って、なんかもっと難しいもんだと思ってた……」とか言ってみたくなるほど簡単で拍子抜けしてしまいそうですね。
それもこれも事後分布も同じ形になるように事前分布を選んだおかげ。特にそういう事前分布は「共役(きょうやく)な事前分布」と呼ばれ、機械学習ではとても重宝されます。
コイン投げの共役事前分布は今回紹介したベータ分布でしたが、元となる問題や分布によって共役事前分布はそれぞれ異なります(例えばサイコロの共役事前分布は「ディリクレ分布」と呼ばれる分布になります)。そういった「他の共役事前分布」はまた機会があるときに紹介します。
まとめ
今回のポイントをまとめておきましょう。
- ベイズ確率は「自信」(信念の度合い)を確率で表したもの
- 確率のルールから事後分布の更新式が得られる
- 事前分布は「なんでもいい」けれど、共役なものを選ぶと計算がとても簡単
そして、コイン投げの共役事前分布であるベータ分布を紹介しました。しかし、そのベータ分布はどんな分布なのか、また2つパラメータαとβをどのように選べばいいか、などは疑問のまま残っています。それらの疑問は、本連載の実践編の中で、実際にベータ分布をいろいろ試しながら確認していく予定です。お楽しみに。
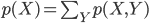
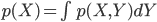
![]()
![]()
![]() ただし
ただし ![]()
![]() ただし
ただし ![]()

![]() ただし
ただし ![]()
![]() ただし
ただし ![]()
![]() を採用して、
を採用して、