お詫びと訂正(正誤表)
本書の以下の部分に誤りがありました。ここに訂正するとともに、ご迷惑をおかけしたことを深くお詫び申し上げます。
(2024年10月30日最終更新)
【第2刷 訂正情報】
P.205「②-2 先頭に挿入するとき」の《ポインタの変更後》の図
| 誤 |
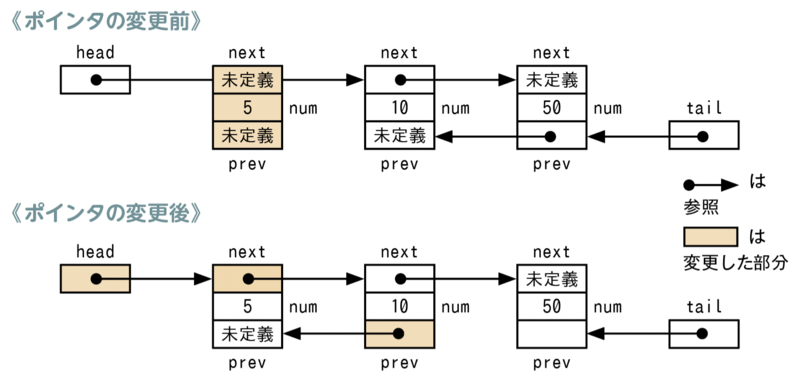 |
|---|
| 正 |
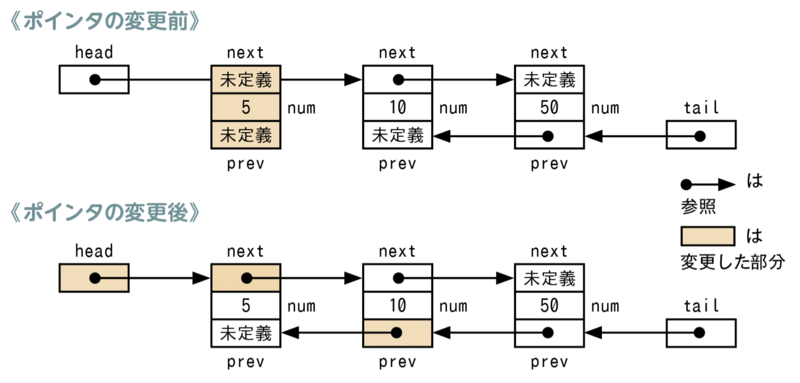 |
|---|
P.143 上図「配列:rank」の右端
【第1刷 訂正情報】(第2刷では修正済み)
P.55「代入文の記述例④」中
| 誤 |
/* 累計金額に合計金額を加算する */ |
|---|
| 正 |
/* 累計額に合計額を加算する */ |
|---|
「金」が2箇所不要です。
P.57「選択処理①の例」中(2箇所)とその1行下(1箇所)
「金」が不要です。
P.58「選択処理②の例」中(4箇所)とその1行下(1箇所)
「金」が不要です。
P.59「選択処理③の例」中(5箇所)とその1~2行下(2箇所)、図表2-3-4の左側の解説中(5箇所)
「金」が不要です。
P.88「2文字目で不一致になったとき」の図
| 誤 |
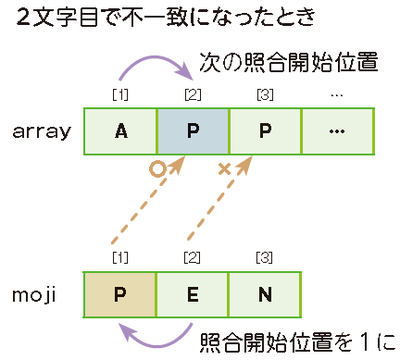 |
|---|
| 正 |
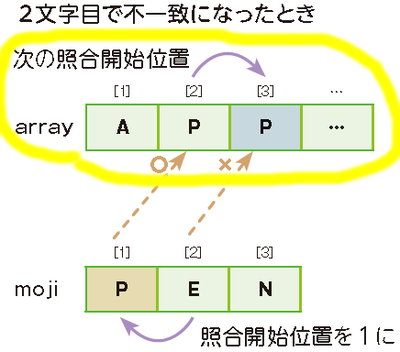 |
|---|
P.215「●二分探索のアルゴリズム」の囲みの(4)
| 誤 |
(4)上記を繰り返して要素が一つだけになったとき、「中央値=検索値」なら値が見つかったことになり、そうでなければ値が見つからなかったことになる。 |
|---|
| 正 |
(4)上記を繰り返し、「中央値=検索値」になる(検索値が見つかった)か、検索範囲の要素が一つだけになったとき(検索値が見つからなかった)に終了。 |
|---|
P.215「〔二分探索の具体例〕」の2行目
P.216 ②、④、⑥の冒頭
P.216 ⑦の説明中
| 誤 |
array[8]=Sで確定します。 |
|---|
| 正 |
array[8]=sarで確定します。 |
|---|
P.234(イ)(ウ)(エ)の図中(3箇所)
P.244 上図の下部の解説
| 誤 |
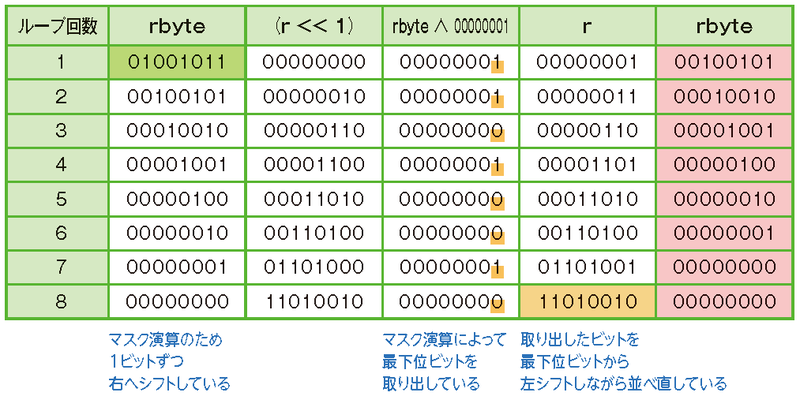 |
|---|
| 正 |
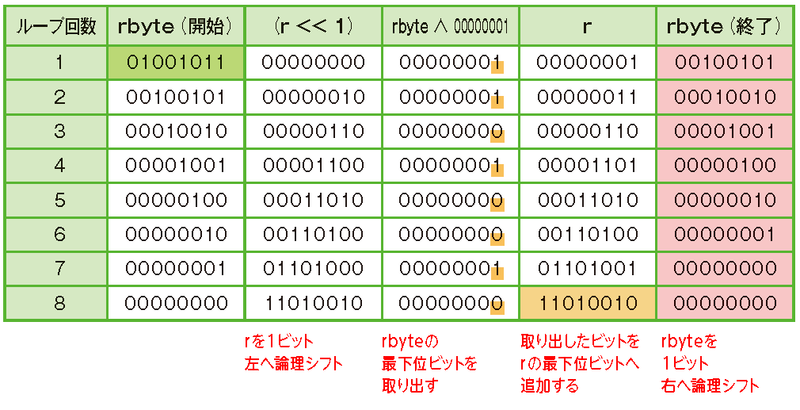 |
|---|
P.244「●求められている動作からプログラムの論理を考える」の4行目
| 誤 |
変数rに最上位ビット(左端)から格納していけば、 |
|---|
| 正 |
変数rに最下位ビット(右端)から格納していけば、 |
|---|
P.244 下図の番号
| 誤 |
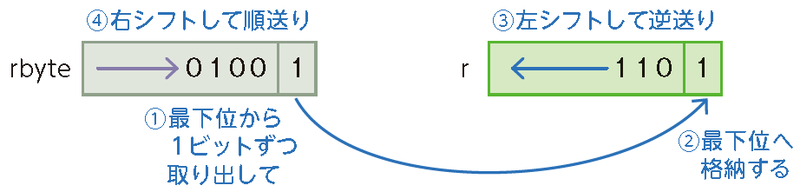 |
|---|
| 正 |
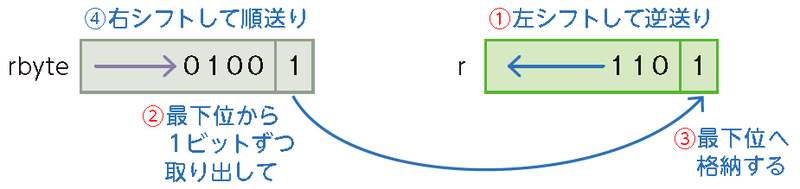 |
|---|
P.209 8~9行目
| 誤 |
(3) (1)と(2)の合計を10 で割った余りを、10 から引いた数字をチェックキャラクターとする。 |
|---|
| 正 |
(3) (1)と(2)の合計を10 で割った余りを、10 から引いた数字をチェックキャラクターとする。なお、10から引いた数字が10のときは0とする。 |
|---|
P.210 〔プログラム〕下から5~6行目
| 誤 |
number ← 10 − (sum mod 10)
ch ← numberを文字に変換
|
|---|
| 正 |
number ← 10 − (sum mod 10)
if (number = 10)
number ← 0
endif
ch ← numberを文字に変換
|
|---|
P.52 「配列要素に値を設定する」の解説7行目
「も」が不要です。
P.52 中程の図。配列seisekiの要素番号[8]の値
P.95 「●配列boxarrayの初期化(4行目)」の説明2~3行目と「●if文を使った多分岐の選択処理」の見出しのカッコ内
P.220 「①文字照合に失敗した場合の移動量の算出」の説明4行目
| 誤 |
移動量:“A”→4、“C”→4、“B”→1“、M”→2 |
|---|
| 正 |
移動量:“A”→1、“C”→2、“B”→4“、M”→4 |
|---|
P.34 3〜4行目
| 誤 |
…進む処理を示しているのでるので迷うことは… |
|---|
| 正 |
…進む処理を示しているので迷うことは… |
|---|
「るので」が不要です。
P.81 一番下の行
「r」が不要です。
P.21 上から6行目
| 誤 |
変数をyを100とし、 |
|---|
| 正 |
変数yを100とし、 |
|---|
「を」が不要です。
P.44 下から7行目
| 誤 |
上記の情報入力~結果算出までの… |
|---|
| 正 |
上記の情報入力~結果出力までの… |
|---|
P.50 「変数を宣言する」の解説4行目
| 誤 |
(前ページ《プログラム名の記述例①》) |
|---|
| 正 |
(p.48《プログラム名の記述例①》) |
|---|
P.58 「2通りの処理に分ける」の解説1行目
| 誤 |
処理を2通りに分けるバターンです。 |
|---|
| 正 |
処理を2通りに分けるパターンです。 |
|---|
P.81 「●処理のポイント」の2~3行目
| 誤 |
1行目から2列目~9列目の… |
|---|
| 正 |
1行目から1列目~9列目の… |
|---|
P.211 下側の図
上段
下段
P.226 図表8-2-6 右端のボックス[9]の下
この記述は不要なので削除
P.246 図表9-2-2 薄緑色で囲った部分
| 誤 |
F(4)=4+F(4-1) |
|---|
| 正 |
F(4)=4×F(4-1) |
|---|
| 誤 |
F(3)=3+F(3-1) |
|---|
| 正 |
F(3)=3×F(3-1) |
|---|
| 誤 |
F(2)=2+F(2-1) |
|---|
| 正 |
F(2)=2×F(2-1) |
|---|
| 誤 |
F(1)=1+F(1-1) |
|---|
| 正 |
F(1)=1×F(1-1) |
|---|







