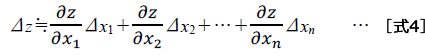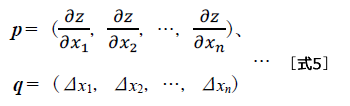機械学習とはコンピュータ自らに学習させることを言います。機械学習に必要な「ベクトル」について見てみましょう。
ベクトルの成分表示
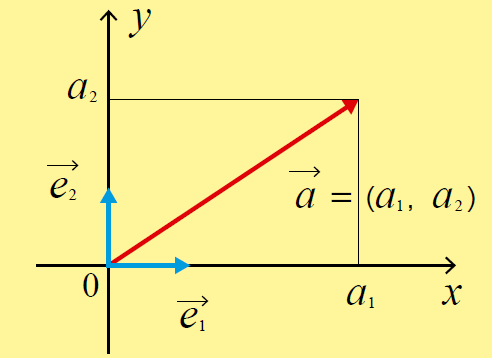
ベクトルは「大きさと方向を持つ量」として定義され、矢のイメージで表現されます。このベクトルの矢を座標平面上に置くことで、ベクトルは座標で表現できます。これをベクトルの成分表示といいます。例えば、平面の場合、ベクトル$a$は次のように表現されます。
図1 ベクトルの成分表示
 【注】「始点を原点にしたときの終点の座標が成分表示」と理解して、応用上問題は起こらない
【注】「始点を原点にしたときの終点の座標が成分表示」と理解して、応用上問題は起こらない
このようにベクトルを成分で表現すると、拡張が容易になります。抽象化して、$n$次元空間のベクトルは次のように表現できます。
$a$$=(a_{1}$、$a_{2}$、$…$、$a_{n}) ……$[式1]
ベクトルの内積
2つのベクトル$a$、$b$のベクトルの内積$a・b$は次のように定義されます。
$a・b$$=|$$a$$||$$b$$|cosθ$($θ$は$a$、$b$のなす角)…… [式2]
図2 ベクトルの内積
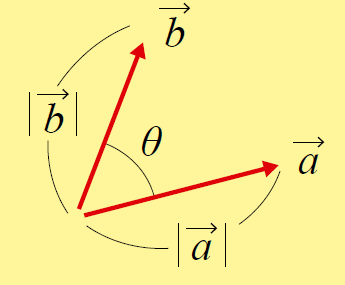 【注】ここで、$|$$a$$|$、$|$$b$$|$はベクトル$a$、$b$の大きさ、すなわち矢の長さを表す
【注】ここで、$|$$a$$|$、$|$$b$$|$はベクトル$a$、$b$の大きさ、すなわち矢の長さを表す
この内積の定義は平面や3次元空間では理解できますが、それ以上になるとイメージしにくくなります。そこで、[式1]の成分で内積[式2]を表してみましょう。
$a$$=(a_{1}$、$a_{2}$、$……$、$a_{n})$、$b$$=(b_{1}$、$b_{2}$、$……$、$b_{n})$のとき、
$a・b$$=a_{1} b_{1}+a_{2} b_{2}+……+a_{n} b_{n} ……$ [式3]
勾配降下法では、関数$z=f(x_{1}$、$x_{2}$、$…$、$x_{n})$の増分$Δz$の近似公式が次のように表されることを利用します。
[式3]と比較すると、次のベクトルの内積$p・q$であることがわかります。
この最初のベクトル$p$は「関数の勾配」と呼ばれるベクトルで、勾配降下法で活躍します。
※以上、『Excelでわかる機械学習超入門』の「巻末付録C」より一部を抜粋。