前回は特別編が加わったため、
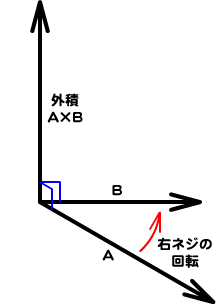
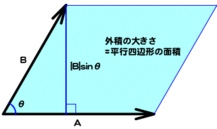
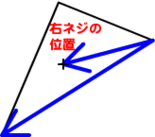
平面上のふたつのベクトルの外積から互いの位置関係がわかる
三角形はもっとも単純な多角形だ。そのため、
ベクトルの外積を使うと、
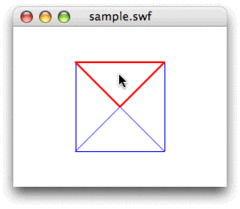
まず、
お題は、
そこで、
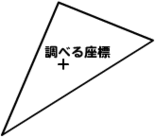
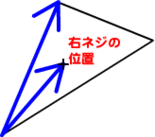
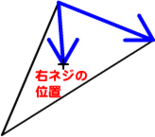
では早速、
function xIsRight(point0:Point, point1:Point):Boolean {
var vector3D_0:Vector3D = new Vector3D(point0.x, point0.y, 0);
var vector3D_1:Vector3D = new Vector3D(point1.x, point1.y, 0);
var crossProduct:Vector3D = vector3D_0.crossProduct(vector3D_1);
var bIsRight:Boolean = (crossProduct.z >= 0);
return bIsRight;
}あいにく、
前述のとおり、
var bResult:Boolean = xIsRight(new Point(0, -1), new Point(1, 0))
trace(bResult); // 出力: trueこの関数ができあがれば、
第1に、
第2は、
必要な機能を関数として定める
初めにも述べたように、
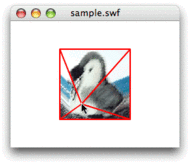
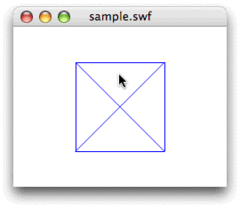
今回のお題は、
// フレームアクション
var nCenterX:Number = stage.stageWidth / 2;
var nCenterY:Number = stage.stageHeight / 2;
var mySprite:Sprite = new Sprite();
var myGraphics:Graphics = mySprite.graphics;
var myTexture:BitmapData = new Image();
var nHalfWidth:Number = myTexture.width / 2;
var nHalfHeight:Number = myTexture.height / 2;
var vertices:Vector.<Number> = new Vector.<Number>();
var indices:Vector.<int> = new Vector.<int>();
var uvData:Vector.<Number> = new Vector.<Number>();
mySprite.x = nCenterX;
mySprite.y = nCenterY;
vertices.push(0, 0);
vertices.push(-nHalfWidth, -nHalfHeight);
vertices.push(nHalfWidth, -nHalfHeight);
vertices.push(nHalfWidth, nHalfHeight);
vertices.push(-nHalfWidth, nHalfHeight);
indices.push(0, 1, 2);
indices.push(0, 2, 3);
indices.push(0, 3, 4);
indices.push(0, 4, 1);
uvData.push(0.5, 0.5);
uvData.push(0, 0);
uvData.push(1, 0);
uvData.push(1, 1);
uvData.push(0, 1);
myGraphics.beginBitmapFill(myTexture);
myGraphics.lineStyle(2, 0xFF0000); // 確認用
myGraphics.drawTriangles(vertices, indices, uvData);
myGraphics.endFill();
addChild(mySprite);
/*
mySprite.addEventListener(MouseEvent.MOUSE_DOWN, xDraw);
function xDraw(eventObject:MouseEvent):void {
vertices[0] = eventObject.localX;
vertices[1] = eventObject.localY;
myGraphics.clear();
myGraphics.beginBitmapFill(myTexture);
myGraphics.drawTriangles(vertices, indices, uvData);
myGraphics.endFill();
}
*/Graphics.
こういうときは、
そこで、
// スクリプト2のフレームアクションに追加
mySprite.addEventListener(MouseEvent.MOUSE_DOWN, xDrawTriangle);
function xDrawTriangle(eventObject:MouseEvent):void {
var nLength:uint = xGetNumTriangles();
for (var i:uint = 0; i < nLength; i++) {
var triangleIndices:Vector.<int> = xGetTriangleAt(i);
trace(triangleIndices);
}
}
function xGetNumTriangles():uint {
var numTriangles:uint = uint(indices.length / 3);
return numTriangles;
}
function xGetTriangleAt(nIndex:int):Vector.<int> {
var nIndices:int = 3;
var n:int = nIndex * nIndices;
var triangleIndices:Vector.<int> = new Vector.<int>(nIndices);
for (var i:uint = 0; i < nIndices; i++) {
triangleIndices[i] = indices[uint(n + i)];
}
return triangleIndices;
}そして、
![図3 インスタンスをクリックすると4つの三角形の3頂点番号の組が[出力]される 図3 インスタンスをクリックすると4つの三角形の3頂点番号の組が[出力]される](/assets/images/dev/serial/01/as3/0055/thumb/TH960_00301.gif)
![図3 インスタンスをクリックすると4つの三角形の3頂点番号の組が[出力]される 図3 インスタンスをクリックすると4つの三角形の3頂点番号の組が[出力]される](/assets/images/dev/serial/01/as3/0055/00302.gif)
あとは、
前掲スクリプト2に、
// フレームアクション
var nCenterX:Number = stage.stageWidth / 2;
var nCenterY:Number = stage.stageHeight / 2;
var mySprite:Sprite = new Sprite();
var myGraphics:Graphics = mySprite.graphics;
var myTexture:BitmapData = new Image();
var nHalfWidth:Number = myTexture.width / 2;
var nHalfHeight:Number = myTexture.height / 2;
var vertices:Vector.<Number> = new Vector.<Number>();
var indices:Vector.<int> = new Vector.<int>();
var uvData:Vector.<Number> = new Vector.<Number>();
mySprite.x = nCenterX;
mySprite.y = nCenterY;
vertices.push(0, 0);
vertices.push(-nHalfWidth, -nHalfHeight);
vertices.push(nHalfWidth, -nHalfHeight);
vertices.push(nHalfWidth, nHalfHeight);
vertices.push(-nHalfWidth, nHalfHeight);
indices.push(0, 1, 2);
indices.push(0, 2, 3);
indices.push(0, 3, 4);
indices.push(0, 4, 1);
uvData.push(0.5, 0.5);
uvData.push(0, 0);
uvData.push(1, 0);
uvData.push(1, 1);
uvData.push(0, 1);
myGraphics.beginBitmapFill(myTexture);
myGraphics.lineStyle(2, 0xFF0000); // 確認用
myGraphics.drawTriangles(vertices, indices, uvData);
myGraphics.endFill();
addChild(mySprite);
mySprite.addEventListener(MouseEvent.MOUSE_DOWN, xDrawTriangle);
function xDrawTriangle(eventObject:MouseEvent):void {
var nLength:uint = xGetNumTriangles();
for (var i:uint = 0; i < nLength; i++) {
var triangleIndices:Vector.<int> = xGetTriangleAt(i);
var triangleVertices:Vector.<Point> = xGetVertices(triangleIndices);
trace(triangleVertices);
}
}
function xGetNumTriangles():uint {
var numTriangles:uint = uint(indices.length / 3);
return numTriangles;
}
function xGetTriangleAt(nIndex:int):Vector.<int> {
var nIndices:int = 3;
var n:int = nIndex * nIndices;
var triangleIndices:Vector.<int> = new Vector.<int>(nIndices);
for (var i:uint = 0; i < nIndices; i++) {
triangleIndices[i] = indices[uint(n + i)];
}
return triangleIndices;
}
function xGetVertices(triangle:Vector.<int>):Vector.<Point> {
var nLength:uint = triangle.length;
var triangleVertices:Vector.<Point> = new Vector.<Point>(nLength);
for (var i:uint = 0; i < nLength; i++) {
var nIndex:int = triangle[i];
var n:int = nIndex * 2;
var myPoint:Point = new Point(vertices[n], vertices[int(n + 1)]);
triangleVertices[i] = myPoint;
}
return triangleVertices;
}![図4 インスタンスをクリックすると4つの三角形の3頂点のxy座標が[出力]される 図4 インスタンスをクリックすると4つの三角形の3頂点のxy座標が[出力]される](/assets/images/dev/serial/01/as3/0055/thumb/TH960_00401.gif)
![図4 インスタンスをクリックすると4つの三角形の3頂点のxy座標が[出力]される 図4 インスタンスをクリックすると4つの三角形の3頂点のxy座標が[出力]される](/assets/images/dev/serial/01/as3/0055/00402.gif)
クリックした三角形にアウトラインを描く
いよいよお題の本丸となる関数
function xInsideTriangle(triangle:Vector.<Point>, myPoint:Point):Boolean {
var nLength:uint = triangle.length;
var pointStart:Point = triangle[nLength - 1];
for (var i:uint = 0; i < nLength; i++) {
var pointEnd:Point = triangle[i];
var point0:Point = pointEnd.subtract(pointStart);
var point1:Point = myPoint.subtract(pointStart);
var bIsRight:Boolean = xIsRight(point0, point1);
if (!bIsRight) {
return false;
}
pointStart = pointEnd;
}
return true;
}三角形の辺のベクトルは、
- 引かれるPointオブジェクト.subtract
(引くPointオブジェクト)
forループの中で、
調べる座標が右ネジの位置になければ、
つぎは、
function xDrawTriangle(eventObject:MouseEvent):void {
var nX:Number = eventObject.localX;
var nY:Number = eventObject.localY;
var pointMouse:Point = new Point(nX, nY);
var nLength:uint = xGetNumTriangles();
for (var i:uint = 0; i < nLength; i++) {
var triangleIndices:Vector.<int> = xGetTriangleAt(i);
var triangleVertices:Vector.<Point> = xGetVertices(triangleIndices);
var bInsideTriangle:Boolean = xInsideTriangle(triangleVertices, pointMouse);
if (bInsideTriangle) {
xDrawOutline(triangleVertices); // 三角形のアウトラインを描く
return;
}
}
}各三角形は互いに重なり合うことはない前提なので、
var outlineSprite:Sprite = new Sprite();
var outlineGraphics:Graphics = outlineSprite.graphics;
mySprite.addChild(outlineSprite);
function xDrawOutline(triangleVertices:Vector.<Point>):void {
var nLength:uint = triangleVertices.length;
var pointLast:Point = triangleVertices[nLength - 1];
outlineGraphics.clear();
outlineGraphics.lineStyle(2, 0x0000FF);
outlineGraphics.moveTo(pointLast.x, pointLast.y);
for (var i:uint = 0; i < nLength; i++) {
var myPoint:Point = triangleVertices[i];
outlineGraphics.lineTo(myPoint.x, myPoint.y);
}
}アウトラインは別のSpriteインスタンス
以上のつくり込みをしたフレームアクション全体が、
// フレームアクション
var nCenterX:Number = stage.stageWidth / 2;
var nCenterY:Number = stage.stageHeight / 2;
var mySprite:Sprite = new Sprite();
var outlineSprite:Sprite = new Sprite();
var myGraphics:Graphics = mySprite.graphics;
var outlineGraphics:Graphics = outlineSprite.graphics;
var myTexture:BitmapData = new Image();
var nHalfWidth:Number = myTexture.width / 2;
var nHalfHeight:Number = myTexture.height / 2;
var vertices:Vector.<Number> = new Vector.<Number>();
var indices:Vector.<int> = new Vector.<int>();
var uvData:Vector.<Number> = new Vector.<Number>();
mySprite.x = nCenterX;
mySprite.y = nCenterY;
vertices.push(0, 0);
vertices.push(-nHalfWidth, -nHalfHeight);
vertices.push(nHalfWidth, -nHalfHeight);
vertices.push(nHalfWidth, nHalfHeight);
vertices.push(-nHalfWidth, nHalfHeight);
indices.push(0, 1, 2);
indices.push(0, 2, 3);
indices.push(0, 3, 4);
indices.push(0, 4, 1);
uvData.push(0.5, 0.5);
uvData.push(0, 0);
uvData.push(1, 0);
uvData.push(1, 1);
uvData.push(0, 1);
myGraphics.beginBitmapFill(myTexture);
myGraphics.drawTriangles(vertices, indices, uvData);
myGraphics.endFill();
addChild(mySprite);
mySprite.addChild(outlineSprite);
mySprite.addEventListener(MouseEvent.MOUSE_DOWN, xDrawTriangle);
function xDrawTriangle(eventObject:MouseEvent):void {
var nX:Number = eventObject.localX;
var nY:Number = eventObject.localY;
var pointMouse:Point = new Point(nX, nY);
var nLength:uint = xGetNumTriangles();
for (var i:uint = 0; i < nLength; i++) {
var triangleIndices:Vector.<int> = xGetTriangleAt(i);
var triangleVertices:Vector.<Point> = xGetVertices(triangleIndices);
var bInsideTriangle:Boolean = xInsideTriangle(triangleVertices, pointMouse);
if (bInsideTriangle) {
xDrawOutline(triangleVertices);
return;
}
}
}
function xDrawOutline(triangleVertices:Vector.<Point>):void {
var nLength:uint = triangleVertices.length;
var pointLast:Point = triangleVertices[nLength - 1];
outlineGraphics.clear();
outlineGraphics.lineStyle(2, 0x0000FF);
outlineGraphics.moveTo(pointLast.x, pointLast.y);
for (var i:uint = 0; i < nLength; i++) {
var myPoint:Point = triangleVertices[i];
outlineGraphics.lineTo(myPoint.x, myPoint.y);
}
}
function xGetNumTriangles():uint {
var numTriangles:uint = uint(indices.length / 3);
return numTriangles;
}
function xGetTriangleAt(nIndex:int):Vector.<int> {
var nIndices:int = 3;
var n:int = nIndex * nIndices;
var triangleIndices:Vector.<int> = new Vector.<int>(nIndices);
for (var i:uint = 0; i < nIndices; i++) {
triangleIndices[i] = indices[uint(n + i)];
}
return triangleIndices;
}
function xGetVertices(triangle:Vector.<int>):Vector.<Point> {
var nLength:uint = triangle.length;
var triangleVertices:Vector.<Point> = new Vector.<Point>(nLength);
for (var i:uint = 0; i < nLength; i++) {
var nIndex:int = triangle[i];
var n:int = nIndex * 2;
var myPoint:Point = new Point(vertices[n], vertices[int(n + 1)]);
triangleVertices[i] = myPoint;
}
return triangleVertices;
}
function xInsideTriangle(triangle:Vector.<Point>, myPoint:Point):Boolean {
var nLength:uint = triangle.length;
var pointStart:Point = triangle[nLength - 1];
for (var i:uint = 0; i < nLength; i++) {
var pointEnd:Point = triangle[i];
var point0:Point = pointEnd.subtract(pointStart);
var point1:Point = myPoint.subtract(pointStart);
var bIsRight:Boolean = xIsRight(point0, point1);
if (!bIsRight) {
return false;
}
pointStart = pointEnd;
}
return true;
}
function xIsRight(point0:Point, point1:Point):Boolean {
var vector3D_0:Vector3D = new Vector3D(point0.x, point0.y,0);
var vector3D_1:Vector3D = new Vector3D(point1.x, point1.y,0);
var crossProduct:Vector3D = vector3D_0.crossProduct(vector3D_1);
var bIsRight:Boolean = (crossProduct.z >= 0);
return bIsRight;
}[ムービープレビュー]で動きを確かめてみよう。テクスチャマッピングされたインスタンスをクリックすると、
次回は、
今回解説した次のサンプルファイルがダウンロードできます。
- スクリプト2~4のサンプルファイル
(CS5形式/約111KB)