前回は前進差分、後退差分の式の導出を行いました。これらは十分に実用的な方法なのですが、更に高い精度を求めたい場合もあるでしょう。今回は、前進差分や後退差分より誤差を小さくできる「中心差分」と、数値微分を行う場合の「微少な量」の決定の仕方を紹介します。
中心差分
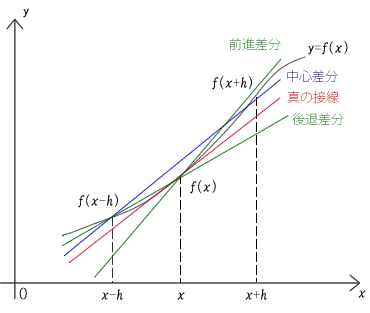
中心差分[1]は、図70.1のように、差分近似を求めたい位置 x の前後 x-h と x+h を取り、関数の描くグラフ上の2つの点をつなげた直線の傾きを、求める微分の近似値とする方法です。この直線の傾きは、前進差分や後退差分の直線と比較して、注目する位置xでの関数の接線の傾きにより近いように見えます。実際に誤差が小さいことを、式を導出することで確認できます。
図70.1 中心差分とは
中心差分の式は、前回導いた式69.5と69.14から、以下のように導きます。誤差のオーダーを再確認するために、 O(h2) はもともとの形にもどします。
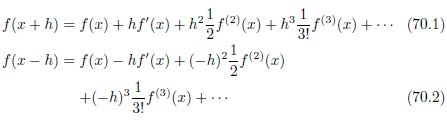
(70.1)-(70.2)
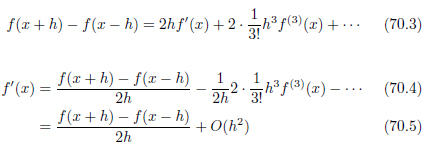
こうして中心差分による導関数の近似式が得られました。誤差の項を見ると、 O(h2) となっています。前進差分や後退差分が O(h) でしたから、より誤差のオーダーが小さいことが分かります[2]。
微少な量hの決定方法
具体的に差分の計算をコンピュータで実行するためには、微少な量hを決定しなければなりません。むやみに小さな値を用いたからといって、精度の良い計算が出来るわけではないからです。
数値微分の誤差はどのようになっているかを見てみましょう。前進差分の場合、先ず近似するために加算を打ち切った微少な項の分の誤差があります。これを打ち切り誤差[3]と言います。
前進差分の場合の打ち切り誤差は、式69.17で示した程度です。これに続くよりちいさな項は問題にしないことにします。

次に、コンピュータに特有の問題、有限長の二進数を用いて数値を表現しますから、桁数からあふれた微少な値は丸めによって切り捨て・切り上げ等の処理をされます。これを丸め誤差[4]と言います。
Java言語で用いる、IEEE754に準拠した浮動小数点数の仮数部は、倍精度で52ビットです。仮数部の最も右のビットのみが1で表せる値、2-52をεで表します[5]。
浮動小数点数で表された関数の値 f(x) には、丸めによって| f(x) | ε 程度の誤差が含まれます。誤差の大きさを知りたいので、関数の値は絶対値をとります。前進差分の式操作により、次の式のように誤差が蓄積します。
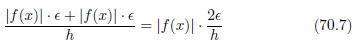
以上二つを合計したのが、前進差分で発生する誤差です。
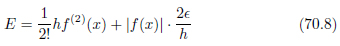
式70.8をhの関数と考えて、Eが最小になるようhを見つけるのです。
図70.2 最小の誤差の見つけ方
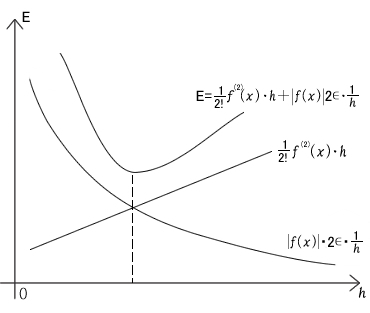
図70.2のように考えると、2つの項が描く2つのグラフの交点の位置のhを求めればよいことが分かります。
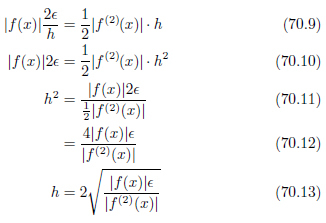
式70.13で得られるhの値の時、誤差は最小となります。
非常に大雑把な見方をし、 f(x) 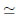 f(2) とすると、この値は次のように変形できます。「
f(2) とすると、この値は次のように変形できます。「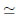 」は「ほぼ等しい」という意味です。
」は「ほぼ等しい」という意味です。

よって、hは ε の倍程度にとれば良いことになります。
誤差については本連載の第10回からを参照してください。
問題 中心差分で誤差最小となるhの値を決定する式を導きましょう。
前進差分の場合を参考に、中心差分の誤差を最小とするhの式を導きましょう。
解説
問題 中心差分で誤差最小となるhの値を決定する式を導きましょう。
中心差分の場合の打ち切り誤差の式は式70.4からわかります。丸め誤差は2hで除することだけが違いです。
打ち切り誤差は式70.4より次の式のようになります。
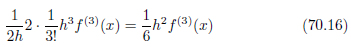
丸め誤差は次の通り。
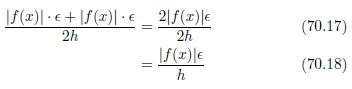
中心差分の丸め誤差の値は、前進差分の場合の半分になっています。
中心差分の誤差はこれらの和です。
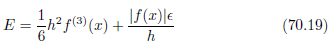
先ほど同様、誤差 Eが最小になるhを求めます。誤差が最小となるのは、| f(3) |の条件の下で、2つの誤差が等しくなるときです。
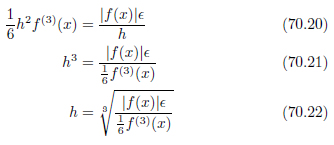
こうして得られたhの値は、大雑把に見積もって| f(x) |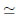 | f(3) |として
| f(3) |として

となります。浮動小数点数ではεより小さな値には意味がないので、結局

が妥当です。前進差分の場合に比較して、微少な量hは半分であることが分かりました。
今回はここまで
いかがだったでしょうか。前回から今回にかけて、差分計算の方法を紹介してきました。ここまでたどり着けば、あとはこの計算方法をプログラムに書き下していけばよいのです。次回は微分の簡単な関数を用いて、筆算した場合と数値計算した場合の比較を行いましょう。

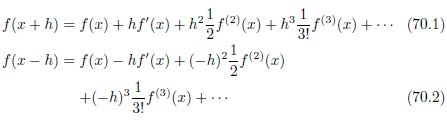
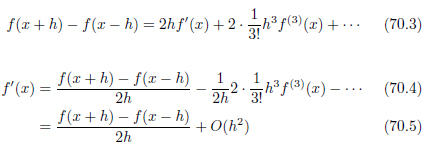
![]()
![]()
![]()

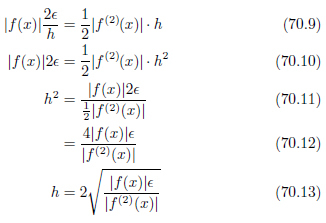
![]() f
f![]() 」
」
![]()
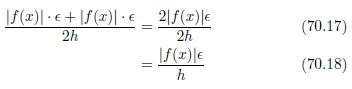
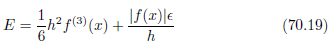
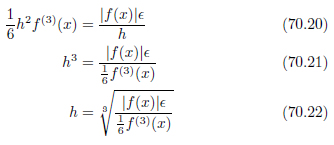
![]() | f
| f![]()
![]()



