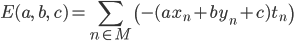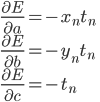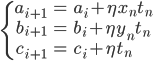前回、分類問題のもっとも簡単なモデルの1つであるパーセプトロンを紹介しました。
今回はそのパーセプトロンの解き方のヒミツを見ていくのですが、その前に機械学習の一般的なお話から入っていきます。
最適化
ここまでの連載の中で「学習」と呼んできたものの正体は、なにがしかの仮定から導き出した誤差関数を最小に、あるいは尤度関数や事後分布を最大にするパラメータを求めることでした。
最大化は、関数全体の符号を反転させれば最小化と同じことになりますから、関数を最小化する点を見つけるための一般的な方法があればとても便利そうです。その「関数の最小点を見つける」ことをこの分野では「最適化」と呼びます。また、最適化を行う対象となる関数は「目的関数」と呼びます。
プログラマが「最適化」という言葉を聞くと、プログラムの実行を高速に、あるいはサイズが最小になるようにコードを書き換える操作(あるいはコンパイラが実行バイナリに対してその操作を行うこと)を一番に思い浮かべるでしょうから、混同しないよう注意しないといけませんね。
機械学習と一口にいっても様々なアプローチがあるのですが、誤差関数/尤度関数/事後分布などの目的関数の最適化問題に落とし込むのは代表的なものの一つと言えるでしょう。
特に線形回帰の目的関数はとても扱いやすい形をしていたので、行列計算一発で最小点を求めることができました。
しかしこのように簡単に解けるのはむしろ例外。パーセプトロンの誤差関数は、前回確認したようにカクカクと折れ曲がった少し面倒な関数なので、そんなに簡単ではありません。
そういう場合にも最小点を求めるにはどうすればよいでしょう。
勾配法
わかりやすさのために、次の図のような1次元空間上の関数f(x)で考えてみましょう。
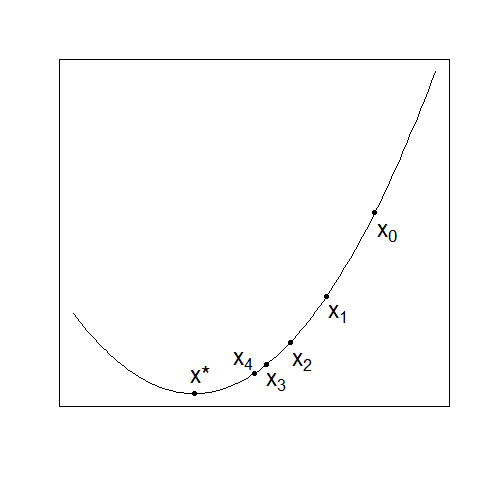
f(x)の最小点はグラフから明らかにx=x*です。つまり、グラフを描くことができれば、最小点は容易に見つけられます。
しかしグラフが描けるとは、空間上のおおむねすべての点で関数の値を評価できるということです。それは1次元や2次元のよく知っている関数であれば可能ですが、次元が上がるほど、関数が複雑になるほど難しくなります。
機械学習や自然言語処理の問題では数百次元、数万次元の空間上の関数を扱うことも珍しくなく、グラフを描くというのは事実上不可能です。
そこで、「グラフ全体を見れば明らか」は禁止した状態で、どうすればこの関数の最小点を求めることができるでしょう。
まずは、思い切って適当な1点を選んでみて、それが最小点であることを期待するという賭けでもしてみましょうか。
えいやと選んだ点はx=x0。残念! 最小点ではありませんでした……。
いやいや、ちょっと待ってください。どうやってx=x0が「最小点ではない」ことがわかったのでしょう。さきほど釘を刺したとおり、「グラフ全体を見れば明らか」は禁止です。
そこでx=x0の周りをちょっとだけ見てみます(グラフ全体は見ていないので大丈夫!)。すると、その左側はx=x0のところより下がっている、つまりより小さい値があります。よってx=x0は最小点ではないことが、グラフ全体を見なくても示せました。
さらに嬉しいことに、x=x0より少し左の点では、値はより小さくなるということもわかります。
では注目点を少し左のx=x1に移して、そこで同じように検討し、またもう少し左のx=x2に……、ということを繰り返していくと、そのうち本当の最小点x=x*にたどり着いてくれそうな気もします。
しかし、まだ詰めの甘いところが2つあります。
まず、「点の周りをちょっとだけ見る」と言いましたが、「ちょっと」というのはどれくらい見ればいいでしょう。
それから「少し左に移す」と言いましたが、その「少し」とはどれくらいなのでしょう。移動幅が小さいとゴールにたどり着くのに時間がかかりすぎ、大きいと肝心の最小点を飛び越してしまいそうです。
「ちょっとだけ周りを見たい」のは、注目している点の左が小さいのか、右が小さいのかを知りたかったわけです。それならその点での傾き、つまり微分を求めればわかりそうです。傾きが正なら左が、負なら右が小さい値、というわけです。
また、例えば上のグラフでの点x=x0と点x=x1を見比べると、どちらも傾きは正ですが、傾きが大きいほど局所解までの距離が遠い傾向があります。必ずこのようになるわけではありませんが、比較的多くの関数が満たす傾向と考えることにします。
そこで傾きに比例した距離だけ動かしてみるという手が考えられます。その比例係数をη>0と書くことにすると、次のように記述できます。
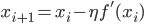
これで傾きが正なら左に、傾きが負なら右に移動した新しい点xi+1が得られるわけです。
このηは「学習率」と呼ばれるのですが、「ηっていくつ?」という話は次回の実践編に譲ります。今は0.1や0.01などの適当な小さめの値を想像しておいてください。
この方法なら、最小点に近づくほど傾きが小さくなることが期待できるので、最小点を飛び越してしまう心配も少なくてすみます。
この操作を続けていき、最終的に点があまり動かなくなったら「収束した」と言って、その点を求めた最小点とするわけです。
ここまで1次元の関数の例で説明しましたが、多次元の関数の場合は各変数による偏微分を並べた「勾配」が傾きに相当します。
例えば3次元関数f(x,y,z)の場合、その勾配は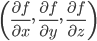 となります。
となります。
すなわち、勾配の方向への移動は次の式で与えられます。
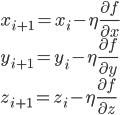
空間が多次元ですから傾きもその次元分のベクトルとなり、最小点候補の移動もベクトル(x,y,z)に対する勾配ベクトルの引き算になるわけですね。
こういったアプローチで最小点を求めようとする手法を総称して「勾配法」と呼びます。
勾配法の問題点
「むむむ、なんだかずいぶん楽観的な方法だなあ。そんなので本当にうまくいくの?」と思われるかもしれません。むしろそれが自然な反応でしょう。
実際、様々なケースで都合の悪いことがおきます。
例えば次の図の(1)のグラフで、出発点をx0の場所に取った場合はおそらくx'を解として求めてしまうでしょうが、これは最小点ではありません。こういった「そこだけみれば最小に見えるけれども、全体の中では最小ではない」点は局所解と呼ばれます。
初期値をx1の場所に取れれば正しい最小点x*にたどり着く可能性は高くなるでしょうが、そのためにはどこに最小値があるのかわかってなければならず、堂々巡りです。
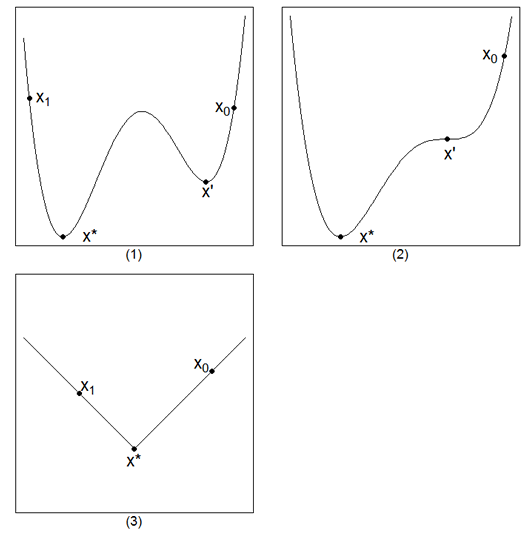
また図の(2)のようなグラフでは傾きが0になるx'の点で動かなくなってしまう可能性がありますし、図の(3)のように折れ曲がったグラフでは、いつまでたっても最小点を飛び越え続けて収束してくれないということも考えられます。
他にも、傾きの小さい状態が延々続くような関数もなかなかゴールにたどり着けないので苦手です。
(3)は要するに微分不可能な点で、最近は様々な対策ができつつあります。また(2)は比較的レアケースなので、気にしなくてもよい(ことにする)方が多いです。
しかし(1)は非常に多くのケース(凸関数と呼ばれる関数を除く)で直面する問題であり、しかも完全な対策はありません。
このようにさまざまな難点を抱えつつも、勾配法は非常によく使われます。
その背景には、解の空間があまりにも高次元すぎ、真の最小解を求めるのは大変高コストで、現実的に不可能と言っていいレベルであることが最初からわかっているという事情があります。
連載の中でも何度か述べたとおり、機械学習ではとにかく「計算できることが正義」ですので、手の届かない真の解を追い求めるよりは、局所解である可能性が高くても、割り切って使うことを良しとするのです。
もちろん、少しでも良い解を得るための努力をしていないわけではなく、勾配法の改良に限らずさまざまなアプローチがありますので、興味のある方は最適化法の教科書をご覧ください。
確率的勾配降下法
そのような勾配法ですが、機械学習の問題にいざ使おうとすると計算が結構大変なことがわかります。
というのも、機械学習の目的関数のほとんどは次のような形をしています。
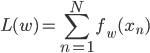
fwはモデルによって一つの点に対する誤差であったり、確率の関数(負の対数尤度)であったりしますが、「各点ごとの値をデータ点の分だけ和をとる」という大枠は共通です。
これを勾配法で解くためにwでの微分を求めても、やはり「データ点の分だけ和をとる」形になっています。
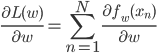
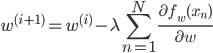
勾配法でパラメータを更新するには、この微分を毎回求めるわけですが、データ点が多いとその個数だけ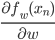 を計算しなくてはいけません。データは10個とか100個ではなく、10,000個、100万個とあったりしますから、とても大変です。
を計算しなくてはいけません。データは10個とか100個ではなく、10,000個、100万個とあったりしますから、とても大変です。
なにかいい方法はないものでしょうか。nで和をとるのが大変なのだから、上の式から単純にΣがなくなったら、次のように簡単になりそうです。
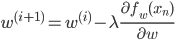
これならデータ点がいくらたくさんあっても一回の計算は超簡単でとてもハッピー……いやいやさすがに、これはまずいでしょう。本当にただΣを取っただけではないですか。残ったnもどうしろというのでしょう。まさかランダムに選ぶとか、いくらなんでもそんなひどい話はあり得ませんよね……?
ところが実はそんなひどい話がまかり通っていまして、一見うまくいくようにはとても見えないこの式が「正しい勾配法」よりもうまくいく場合も珍しくなく、もちろん計算はものすごく速い、というのですから本当に困ってしまいます。
というわけで名前も付いていて、「確率的勾配降下法」と呼びます。一方、Σが残っている「一番素直な勾配法」は「最急降下法」と呼びます。
nはやはりすべての値をぐるっと一周するのですが、順番は本当にランダムで、むしろその方がいいことが知られています。名前に「確率的」とついているのは、実行する度に結果が変わることを表しています。
ちなみに「確率的~」という名称は、いわゆる確率を組み込んだモデルを表す場合と、乱数を使っていて実行する度に結果が異なるアルゴリズムを表す場合があり、ややこしいです(名前を分けて欲しいですよね)。
話を元に戻して、nをぐるっと一周回しただけでうまく行くなんてことはさすがになく、データ全体を何周か計算させる必要はどうしてもあります。それでも最急降下法の1回分と同じ計算量でN回移動できるおかげで、非常に速く局所解の周りにたどり着くことが期待できるのです。
データ点xnごとにfw(xn)のwに関する最小点は異なりますから、確率的勾配降下法では点を動かす度に異なる目標に近づこうとするようなものです。それでも全体を平均すればだいたいうまくいくというのが確率的勾配降下法の主張です。それだけではなく、毎回目標が異なるおかげで、局所解に引っかかりやすいという勾配法最大の弱点をそこそこ回避できる(可能性がある)という特徴も備えています。
一方、毎回目標が異なるおかげで、いつまでたっても点がうろうろと動き続けて「収束」しないという振る舞いもになります。そこで一般には、データを一周回す度に学習率ηを適当に小さくしてあげるという対策が必要になります。
確率的勾配降下法の性質について、いくつかの限定的なケースについては理論的に確かめられている部分もあるのですが、ほとんどは「経験的によい性質を持つことが知られている」という範囲にとどまります。便利で強力な手法ですが、決して最適解を求めているわけではないことは念頭に置いて使うべきでしょう。
ちなみに、このようにデータ全体をまとめて使うのではなく、一件ずつ使って学習することを「オンライン学習」と呼びます。コンピュータ業界で使われる「オンライン」という言葉とは意味がかなり違うので、「最適化」に引き続き注意しなくてはいけませんね。
パーセプトロンの場合
さて、前回紹介したパーセプトロンの解き方を勾配法から見直してみましょう。
パーセプトロンでは、xnでの誤差を次のように仮定しました。
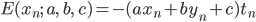 :予測が間違っているとき
:予測が間違っているとき
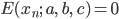 :予測が正しいとき
:予測が正しいとき
したがって誤差関数は次のようになります。
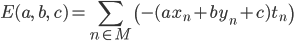 ただし Mはパラメータa,b,cの元で不正解になるデータ(xn,yn,tn)を与えるnの集合とします。
ただし Mはパラメータa,b,cの元で不正解になるデータ(xn,yn,tn)を与えるnの集合とします。
この誤差関数Eを目的関数とした最適化問題を確率的勾配降下法で解いてみましょう。
確率的勾配降下法ですから、和をとる前のE(xn;a,b,c)をa,b,cで偏微分する必要があります。
予測が正解していればE(xn;a,b,c)=0であり、その偏微分も0ですから、不正解の場合のみ考えればよいことになります。
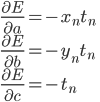
このことから、確率的勾配降下法による更新式は次のようになります。
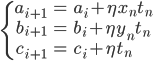
この式のηを1にすれば、前回紹介したパーセプトロンの学習式が得られます。
先ほど、確率的勾配降下法では一般的に学習率ηは小さくしていくという話をしたばかりですが、パーセプトロンの場合は特別にη=1に固定します。というのも、「データが線形分離可能ならば、η=1で固定のときにこのアルゴリズムは有限回で停止する(すべての予測が正解する)」ことが示されているからです(パーセプトロンの収束定理)。
これはパーセプトロンのこのアルゴリズムに特化したアプローチで示されているもので、一般の問題について確率的勾配降下法が収束を保証されることはまずありません。
パーセプトロンの学習アルゴリズムは、いろんな意味で確率的勾配降下法の特殊例ということなのです。
今回紹介した確率的勾配降下法は、このあとロジスティック回帰の学習にて活躍する予定ですが、その前に次回は実践編としてパーセプトロンを実装してみることにします。お楽しみに。

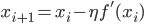
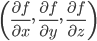 となります。
となります。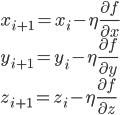

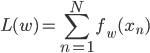
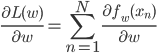
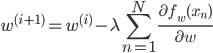
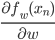 を計算しなくてはいけません。データは10個とか100個ではなく、
を計算しなくてはいけません。データは10個とか100個ではなく、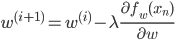
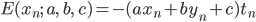 :予測が間違っているとき
:予測が間違っているとき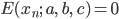 :予測が正しいとき
:予測が正しいとき