少し間が空いてしまいましたが、
環境はこれまでと同じくPython/
パーセプトロンの復習
第15回で紹介したパーセプトロンの学習アルゴリズムをもう一度簡単に振り返っておきましょう。
2次元平面上のデータ点(xn,yn)(n=1,…,N)に正解ラベルtn∈{+1,-1}が与えられているとします。パーセプトロンは、
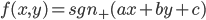
そのようなパラメータは、
データの中からランダムに1点(xn,yn)を取り出し、
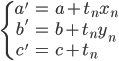
続いてまた別のデータ点をランダムに取って、
すべてのデータ点について
ここまで、
D次元空間の点xnに対して、
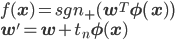
これらを使って、
パラメータベクトルwの次元は、
パーセプトロンの実装
それではパーセプトロンを実装していきますが、
一般にプログラムを書くとき、
ところがこういったアルゴリズムのとき、
しかし慣れてないとそのあたりがわかりませんから、
そこで今回はまず中核となるところを実装して、
さて、
ここでは簡単のためデータ点が2次元空間上にある場合を実装するのですが、
というわけで、
import numpy as np
# データ点を特徴ベクトルに変換
def phi(x, y):
return np.array([x, y, 1])φの引数のデータ点をベクトルで与える場合は、
# 末尾に定数項にあたる 1 を付け加えるバージョン
# (今回はこちらは使いません)
def phi(x):
return np.concatenate((x, [1]))次は予測とパラメータの更新を書きます。数式を素直に実装するとこうなります。
# 予測
predict = np.sign((w * phi(x_n, y_n)).sum())
# 予測が不正解なら、パラメータを更新する
if predict != t_n:
w += t_n * phi(x_n, y_n)こうしてみると、
その中で一番簡単なのはwですから、
w = np.zeros(3) # 3次の 0 ベクトルデータは2次元空間ですが、
次にデータ点(xn,yn)や正解tnですが、
いえ、
Pythonで0からN-1までの配列を作るにはrange関数を、
import random
w = np.zeros(3) # 3次の 0 ベクトル
list = range(N)
random.shuffle(list)
for n in list:
x_n = X[n]
y_n = Y[n]
t_n = T[n]
# 予測
predict = np.sign((w * phi(x_n, y_n)).sum())
# 予測が不正解なら、パラメータを更新する
if predict != t_n:
w += t_n * phi(x_n, y_n)さらに
while True:
list = range(N)
random.shuffle(list)
misses = 0 # 予測を外した回数
for n in list:
x_n, y_n = X[n, :]
t_n = T[n]
# 予測
predict = np.sign((w * phi(x_n, y_n)).sum())
# 予測が不正解なら、パラメータを更新する
if predict != t_n:
w += t_n * phi(x_n, y_n)
misses += 1
# 予測が外れる点が無くなったら学習終了(ループを抜ける)
if misses == 0:
break人工データの生成
これでxn, yn, tn, wは解決しましたが、
そこで何でもいいから適当なデータを取ってきて……いえいえ、
しかし、
2次元空間上の点(x,y)をランダムに100個生成し、
そういったデータ{(xn,yn)}とT={tn}を生成するためのスクリプトは次のようになります。
# データ点の個数
N = 100
# ランダムな N×2 行列を生成 = 2次元空間上のランダムな点 N 個
X = np.random.randn(N, 2)
def h(x, y):
return 5 * x + 3 * y - 1 # 適当に決めた真の分離平面 5x + 3y = 1
T = np.array([ 1 if h(x, y) > 0 else -1 for x, y in X])ランダムなデータ点の生成には、
このように乱数を使って人工データを作ることはとても一般的なのですが、
# データ点のために乱数列を固定(シードに 0 を与える場合)
np.random.seed(0)プログラムの途中でまた
シードを0にした場合のデータ点の分布は次のようになります。t=+1である点は赤、
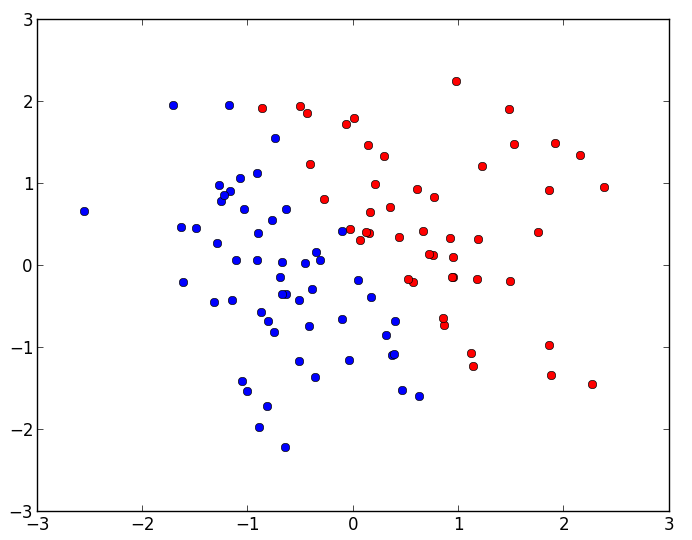
ところでここで書いた生成方法だと2次元のデータ点を一つの変数Xに入れているため、
# 修正前
x_n = X[n]
y_n = Y[n] # 修正後
x_n, y_n = X[n,:]最初からデータ構造をどのように実装するか設計しておけば、
今回の手順のように、
最後に、
# 図を描くための準備
seq = np.arange(-3, 3, 0.02)
xlist, ylist = np.meshgrid(seq, seq)
zlist = [np.sign((w * phi(x, y)).sum()) for x, y in zip(xlist, ylist)]
# 分離平面と散布図を描画
plt.pcolor(xlist, ylist, zlist, alpha=0.2, edgecolors='white')
plt.plot(X[T== 1,0], X[T== 1,1], 'o', color='red')
plt.plot(X[T==-1,0], X[T==-1,1], 'o', color='blue')
plt.show()これらのコードの部品をつなげた、
import numpy as np
import matplotlib.pyplot as plt
import random
# データ点の個数
N = 100
# データ点のために乱数列を固定
np.random.seed(0)
# ランダムな N×2 行列を生成 = 2次元空間上のランダムな点 N 個
X = np.random.randn(N, 2)
def h(x, y):
return 5 * x + 3 * y - 1 # 真の分離平面 5x + 3y = 1
T = np.array([ 1 if h(x, y) > 0 else -1 for x, y in X])
# 特徴関数
def phi(x, y):
return np.array([x, y, 1])
w = np.zeros(3) # パラメータを初期化(3次の 0 ベクトル)
np.random.seed() # 乱数を初期化
while True:
list = range(N)
random.shuffle(list)
misses = 0 # 予測を外した回数
for n in list:
x_n, y_n = X[n, :]
t_n = T[n]
# 予測
predict = np.sign((w * phi(x_n, y_n)).sum())
# 予測が不正解なら、パラメータを更新する
if predict != t_n:
w += t_n * phi(x_n, y_n)
misses += 1
# 予測が外れる点が無くなったら学習終了(ループを抜ける)
if misses == 0:
break
# 図を描くための準備
seq = np.arange(-3, 3, 0.02)
xlist, ylist = np.meshgrid(seq, seq)
zlist = [np.sign((w * phi(x, y)).sum()) for x, y in zip(xlist, ylist)]
# 分離平面と散布図を描画
plt.pcolor(xlist, ylist, zlist, alpha=0.2, edgecolors='white')
plt.plot(X[T== 1,0], X[T== 1,1], 'o', color='red')
plt.plot(X[T==-1,0], X[T==-1,1], 'o', color='blue')
plt.show()パーセプトロンの役割
このコードを実行すると、
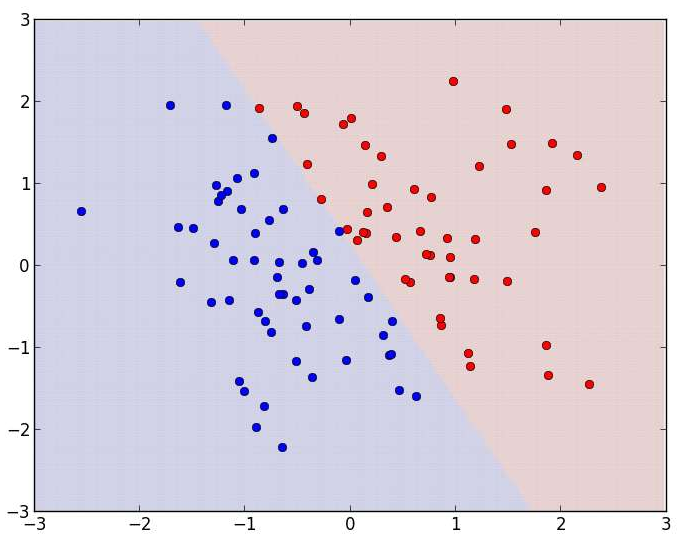
このように
そんな直線があることくらいグラフを見れば一目でわかってしまうのに、
ここでは2次元のデータを使っていますからグラフが描けますが、
パーセプトロンの感じをつかむためにも、
中でも、
ただしその場合は、
具体的には、
#while True:
for i in xrange(1000): # 1000 回までデータを回して学習次回はロジスティック回帰を紹介します。この連載で扱う最後のモデルになる予定です。お楽しみに。



