今回は実践編、
環境はこれまでと同じくPython/
パーセプトロンの実装の復習
今回のロジスティック回帰の実装は、
そこでパーセプトロンの実装を再掲しておきます。パーセプトロンそのものの復習はここではしませんので、
import numpy as np
import matplotlib.pyplot as plt
import random
# データ点の個数
N = 100
# データ点のために乱数列を固定
np.random.seed(0)
# ランダムな N×2 行列を生成 = 2次元空間上のランダムな点 N 個
X = np.random.randn(N, 2)
def h(x, y):
return 5 * x + 3 * y - 1 # 真の分離平面 5x + 3y = 1
T = np.array([ 1 if h(x, y) > 0 else -1 for x, y in X])
# 特徴関数
def phi(x, y):
return np.array([x, y, 1])
w = np.zeros(3) # パラメータを初期化(3次の 0 ベクトル)
np.random.seed() # 乱数を初期化
while True:
list = range(N)
random.shuffle(list)
misses = 0 # 予測を外した回数
for n in list:
x_n, y_n = X[n, :]
t_n = T[n]
# 予測
predict = np.sign((w * phi(x_n, y_n)).sum())
# 予測が不正解なら、パラメータを更新する
if predict != t_n:
w += t_n * phi(x_n, y_n)
misses += 1
# 予測が外れる点が無くなったら学習終了(ループを抜ける)
if misses == 0:
break
# 図を描くための準備
seq = np.arange(-3, 3, 0.02)
xlist, ylist = np.meshgrid(seq, seq)
zlist = np.sign((w * phi(xlist, ylist)).sum())
# 分離平面と散布図を描画
plt.pcolor(xlist, ylist, zlist, alpha=0.2, edgecolors='white')
plt.plot(X[T== 1,0], X[T== 1,1], 'o', color='red')
plt.plot(X[T==-1,0], X[T==-1,1], 'o', color='blue')
plt.show()ロジスティック回帰の実装
これをロジスティック回帰の実装に差し替えるにあたって、
順に見ていきましょう。
人工データの生成
パーセプトロンは線形分離可能な問題しか解けなかったので
一方、
というわけでデータ生成のコードは基本そのまま使いますが、
パーセプトロンの正解ラベルは+1と-1であるのに対し、
TT = np.array([ 1 if f(x, y) > 0 else 0 for x, y in X])これに関連して、
パーセプトロンによって得られる予測は
よって、
plt.imshow(zlist, extent=[-3,3,-3,3], origin='lower', cmap=plt.cm.PiYG_r)imshow関数は、
予測確率とパラメータの更新式
パーセプトロンにしてもロジスティック回帰にしても、
パーセプトロンのコードでは、
一方、
ロジスティック回帰の予測確率は次の式で表されるのでした。
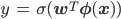
ただし 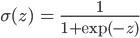
これを実装するには、
せっかくですから関数として実装しておきましょう。
# シグモイド関数
def sigmoid(z):
return 1.0 / (1.0 + np.exp(-z))上の式では予測確率にyの文字が当てられていますが、
φnもこの後またすぐ使いますから、
# 特徴量と予測確率
feature = phi(x_n, y_n)
predict = sigmoid(np.inner(w, feature))特徴関数phiは定数項にあたる1を付け加えただけの、
予測確率がわかると、
ロジスティック回帰の確率的勾配降下法では、
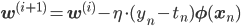
ηは
# 学習率の初期値
eta = 0.1 # イテレーションごとに学習率を小さくする
eta *= 0.9このetaを使ってパラメータを更新します。
w -= eta * (predict - t_n) * featureパラメータの初期値と学習の終了条件
後はパラメータwの初期化と学習の終了条件だけです。この2つは実は少々関連があります。
パーセプトロンの解法アルゴリズムは、
この時の学習ループの終了条件は明確で、
一方の確率的勾配降下法で求まるのは、
w = np.random.randn(3) # パラメータをランダムに初期化そうして求めた局所解は、
そこで確率的勾配降下法では尤度などの指標値があまり変化しなくなったら終了したり、
今回はシンプルに学習回数を50周と決めておきましょう。
これらをすべて反映したコードは次のようになります。
import numpy as np
import matplotlib.pyplot as plt
# データ点の個数
N = 100
# データ点のために乱数列を固定
np.random.seed(0)
# ランダムな N×2 行列を生成 = 2次元空間上のランダムな点 N 個
X = np.random.randn(N, 2)
def f(x, y):
return 5 * x + 3 * y - 1 # 真の分離平面 5x + 3y = 1
T = np.array([ 1 if f(x, y) > 0 else 0 for x, y in X])
# 特徴関数
def phi(x, y):
return np.array([x, y, 1])
# シグモイド関数
def sigmoid(z):
return 1.0 / (1 + np.exp(-z))
np.random.seed() # 乱数を初期化
w = np.random.randn(3) # パラメータをランダムに初期化
# 学習率の初期値
eta = 0.1
for i in xrange(50):
list = range(N)
np.random.shuffle(list)
for n in list:
x_n, y_n = X[n, :]
t_n = T[n]
# 予測確率
feature = phi(x_n, y_n)
predict = sigmoid(np.inner(w, feature))
w -= eta * (predict - t_n) * feature
# イテレーションごとに学習率を小さくする
eta *= 0.9
# 図を描くための準備
seq = np.arange(-3, 3, 0.01)
xlist, ylist = np.meshgrid(seq, seq)
zlist = [sigmoid(np.inner(w, phi(x, y))) for x, y in zip(xlist, ylist)]
# 散布図と予測分布を描画
plt.imshow(zlist, extent=[-3,3,-3,3], origin='lower', cmap=plt.cm.PiYG_r)
plt.plot(X[T==1,0], X[T==1,1], 'o', color='red')
plt.plot(X[T==0,0], X[T==0,1], 'o', color='blue')
plt.show()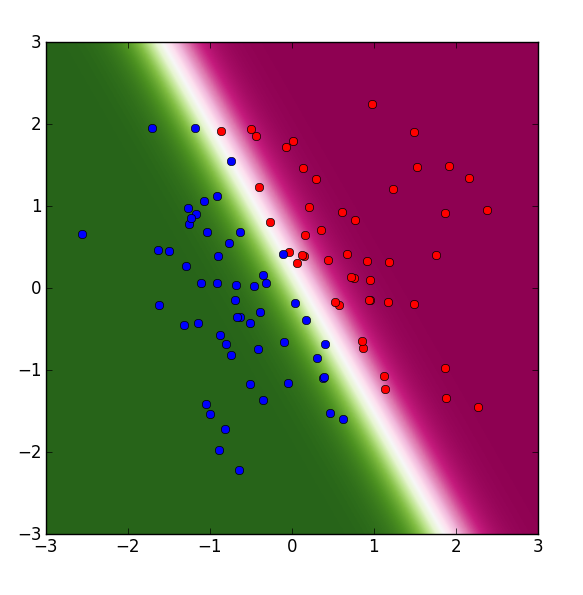
さて、
最終回は連載の流れの中では触れられなかった落ち穂拾いをしつつ、



