稠密性（ちょうみつせい）について

前回から見えるように、整数から有理数へ範囲を広げることの利点は非常に大きいのですが、その理由は、有理数が整数にはない稠密性（ちょうみつせい：density）という性質を持っていることにあります。あまり日常で使う言葉ではありませんが、直感的に言えば物がぎっしり詰まっているということです。もう少し数学的に厳密に書くと、

• x<yを満たす任意の数x、yについて、x<m<yとなる数mが存在する

となります。平たく言えば、どんな2つの数の間（区間）にも、まだまだ無限に数がある、ということです。

ここでキーとなるのは「任意の」という言葉です。特定のx, yではなく、大小関係を満たすあらゆる数のペアについて成立することがキモです。たとえば、1と2の間には、0.5という数が存在します。今度は1と0.5の間で見ても、0.25というさらに中間の数が存在します。後は同じ手順で、1と0.25の間には0.125、1と0.125の間には0.0625…と無限に続けられます（図7⁠）⁠。

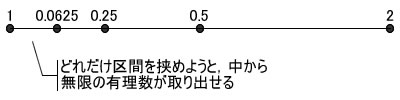
すなわち稠密性とは、夢のようなリソース無限の原則なのです。私たちは、すぐに枯渇する整数の井戸とは違う、汲めども尽きぬ魔法の泉を手に入れてしまったのです[3]⁠。

なおこれは余談ですが、上記の話からゼノンのパラドックスを想起した人もいるでしょう。「⁠アキレスは絶対に亀に追いつけない」とか「飛ぶ矢は静止している」という、あれです。あの逆説の鍵もまた、「⁠どれほど微小な区間にも無限の点が含まれている」という空間の稠密性を前提していることにありました。神速のアキレスといえども、無限の点を走破することはできない。よって、アキレスは亀に追いつけない、というわけです。

しかし、アキレスにとっては致命傷になったこの特性も、DBエンジニアにとっては天の恵みです。ありがたく利用させていただきましょう。