フラクタルとしての入れ子集合
フラクタル
入れ子区間モデルでノードを挿入するときに重要な役割を果たす公式ⓐとⓑ(第6回 SQLで木構造を扱う~入れ子区間モデル(1)参照)は、区間(線分)を3分するための2点を与えるものです。そしてこれを繰り返し適用すると、同じ構造を持つ小さな入れ子集合を次々と作ることができます。
このような自己相似的な図形をフラクタルと呼びます。フランスの数学者マンデルブロが1977年に一般化した概念で、日本でも一時期はやりました。海岸線や樹木の形など自然界にも多く存在する形状ですが、それだけでなく経済活動など人間社会にもこれに近似した現象が観察できることで知られています[4](図8)。
図8 フラクタル図形の一種:シェルピンスキーのギャスケット
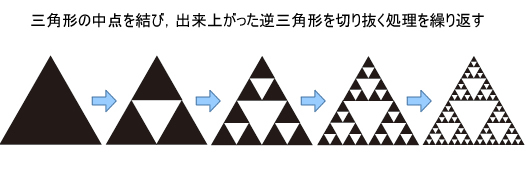 ※ この図は、Wikipedia日本語版の「シェルピンスキーのギャスケット」に掲載されている図をベースにアレンジしています。
※ この図は、Wikipedia日本語版の「シェルピンスキーのギャスケット」に掲載されている図をベースにアレンジしています。
カントール集合
実は、カントールもまた、線分を三等分して真ん中を抜くという作業を繰り返して作られるフラクタル集合を考えています(まだ「フラクタル」という概念が知られていない時代に)。一般にカントール集合と呼ばれているもので、これが入れ子区間モデルのもう一つの源泉です。
図9を見るとわかるように、カントール集合が線分の真ん中を捨てて作られる構造であるのに対し、入れ子区間モデルは反対にその不要部分を有効資源として活用しています。つまり、入れ子集合はカントール集合の裏返しで、両者は「ルビンの壷」のような地と図の関係にあります。
図9 カントール集合
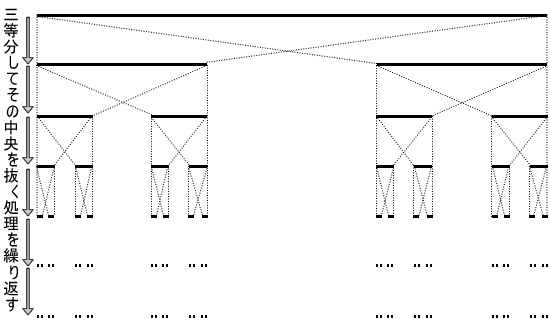 ※ この図は、Wikipedia日本語版の「カントール集合」に掲載されている図をベースにアレンジしています。
※ この図は、Wikipedia日本語版の「カントール集合」に掲載されている図をベースにアレンジしています。
終わりに
本稿では、入れ子区間モデルが入れ子集合モデルの一般化であり、ノード挿入時のパフォーマンス低下やロック競合の問題を大きく軽減するメリットを持つことを解説してきました。
本文で述べたとおり、入れ子区間モデル(入れ子集合モデル)は、カントールが100年以上前に用意していた、整数から有理数への一般化とカントール集合という2つのアイデアにその起源を求められます。彼はもちろん数学史に名を刻む大数学者ですが、私たちは今でもその影響下にいます。そしてそのアイデアが、フラクタルなどの隣接分野ともリンクして発展していく様はなかなかスリリングなものがあります。読者の皆さんに、そういう「大いなる連環」のつながりの一つを感じていただけたなら幸いです。
参考資料
- Joe Celko著『Joe Celko's Trees and Hierarchies in SQL for Smarties』
(Morgan Kaufmann Pub, 2004)
- 有理数を利用した入れ子区間モデルについては、「5.4 Rational Numbers and Nested Intervals Model」を参照。本書はもちろん全体としても名著ですが、その中でも本節は白眉(はくび)です。
- 野矢茂樹著『無限論の教室』
(講談社, 1998)
- 対角線論法のイメージについてのわかりやすい解説が得られます。対話形式で楽しく読めるので入門に良いでしょう。集合論を整数から有理数、実数へ一般化する道筋についても(数式がないためかえって少しわかりにくいが)説明があります。





