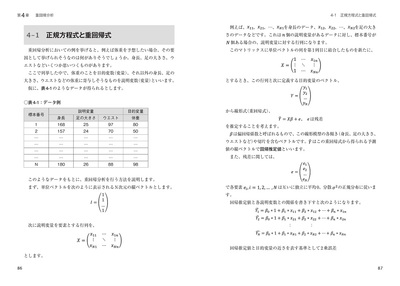
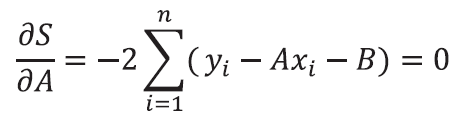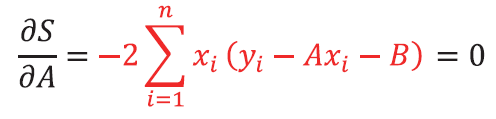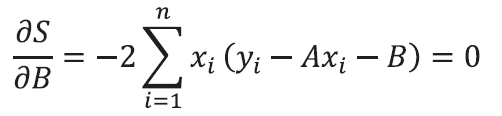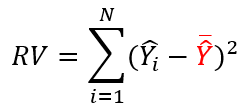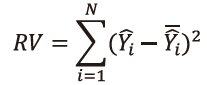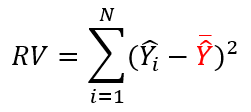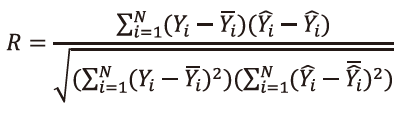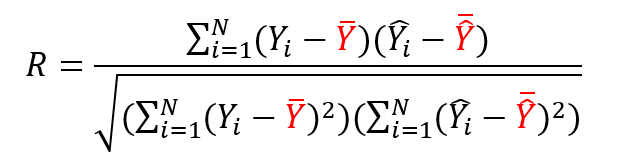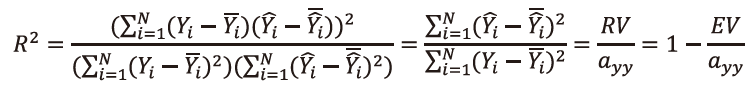書籍概要

機械学習・統計処理のための数学入門
――基本演算からRプログラミングまで

著者
発売日
更新日

概要

数学の素養があるだけではデータサイエンスのプロとは言えません。なぜなら，実際の数理モデル開発やデータ分析では，組み合わせ方やプログラミングの知識が必要になるためです。また，データ分析では，数値微分・数値積分の知識がプログラミングで計算する際には非常に役立ちます。そこで本書では，数値計算やパラメータ計算法などを説明したあとに，応用編として現場で利用されるデータ分析方法を取り上げます。具体的には「対数尤度（ゆうど）の最大化法と重回帰」「一般化線形モデル」「多クラス回帰モデル」「Bradley-Terry model」「2元表の解析モデル」「生存時間解析（ワイブル分布）」で，Rによる数値計算のプログラムも併記しています。本書を活用していただくと，例えば機械学習モデルのパラメータを導く際に必要な二階偏微分を要素とする行列（ヘッセ行列など）の計算が非常にラクになり，データサイエンスにおけるプログラミングで数値微分・数値積分や数値計算そのものの重要さを再確認できるでしょう。
なお，本書は，大学の初等数学程度の知識を前提としています。

こんな方におすすめ

  • データ分析のための数学を学び直したい方（大学の初等数学程度の知識を前提）
  • 現場で使うデータ分析手法（組み合わせ方）を学びたい方
  • データ分析の基本演算（微分積分）をRでプログラミングしたい方

サンプル

samplesamplesamplesamplesample

目次

第1章　Rプログラミング環境の準備

  • 1-1　Rのセットアップ
    • ダウンロード
    • インストール
  • 1-2　RStudioのセットアップ
    • ダウンロード
    • インストール
  • 1-3　Rの動作確認
    • まずはHello World
  • 1-4　本書で使用するパッケージの追加

第2章　数値計算

  • 2-1　差分と差分商
    • 差分商とは
    • 差分とは
  • 2-2　微分と偏微分
  • 2-3　数値積分
    • ラグランジュの内挿公式
    • ニュートン・コーツの積分公式
    • 重積分

第3章　ニュートン法・反復法

  • 3-1　ニュートン法（ニュートンラフソン法）
    • テイラー展開とニュートン法（ニュートンラフソン法）
  • 3-2　多変数ニュートン法
    • 2変数テイラー展開
  • 3-3　準ニュートン法
    • Broyden Quasi-Newton Algorithm（ヤコビアンの逆行列の近似行列Hを計算）
    • Pre-Broyden Algorithm（ヤコビアンの近似行列Bを計算）
    • fiacco, mccormick（1968），sargent（1969），murtagh（ヘッシアンの逆行列の近似行列）
    • その他の反復法

第4章　重回帰分析

  • 4-1　正規方程式と重回帰式
    • 偏差積和行列を用いる方法
  • 4-2　分散分析
  • 4-3　重相関係数
    • 出力結果
  • 4-4　偏回帰係数の検定
    • 野球のデータ
    • 交通事故死傷者数の予測データ

第5章　一般化線形モデル

  • 5-1　指数分布族
  • 5-2　連結関数（link function）
    • 例1　ポアソン回帰
    • 例2　正規回帰モデル
  • 5-3　フィッシャー・スコア法
    • 例1　対数尤度が2項分布に従う場合～ロジット変換（2項回帰モデル）
    • 例2　ポアソン回帰モデル
    • 例3　ロジスティックモデル・プロビットモデル・補対数対数モデル
    • 例4　指数回帰モデル
    • 例5　ガンマ分布回帰
    • 例6　逆ガウス分布回帰

第6章　多クラスロジスティック

  • 6-1　ベルヌーイ・ロジットモデルの多クラス拡張
  • 6-2　データ処理の例

第7章　Bradley-Terry model

  • 7-1 データの説明
  • 7-2 仮説検定
    • 出力結果
  • 7-3　各反復法
    • Broyden Quasi-Newton Algorithm
    • fiacco, mccormick（1968），murtagh, sargent（1969）
    • levenberg（1944）

第8章　主成分分析

  • 8-1　主成分導出
  • 8-2　ラグランジュ関数をもとにした考え方
  • 8-3　固有値，および固有ベクトルの計算

第9章　2元表の解析モデル

  • 9-1　主効果と交互作用を含めた回帰モデル
  • 9-2　尤度比検定
    • データの説明
    • 準ニュートン法
    • 重み付き最小二乗法

第10章　比例危険度モデル（ワイブル分布）

  • 10-1　生存時間解析によるモデル，比例危険度モデルの最尤推定
  • 10-2　データの説明

サポート

ダウンロード

サンプルコードについて

（2021年3月3日更新）

本書のサンプルソースがダウンロードできます。解凍してできたファイル名はリスト番号になっています。

ダウンロード
Rcode_20210303.zip

なお，サンプルソース（.Rファイル）の文字コードは「UTF-8」です。RStudioに読み込んだ際に文字化けする場合は，［File］→［Reopen with Encoding...］で「UTF-8」を選択してください。

正誤表

本書の以下の部分に誤りがありました。ここに訂正するとともに，ご迷惑をおかけしたことを深くお詫び申し上げます。

（2021年4月20日最終更新）

P.76　上から1番目の数式

誤

誤

正

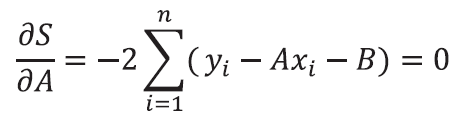
正

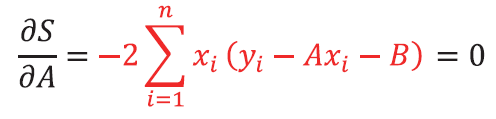
P.76　上から2番目の数式

誤

誤

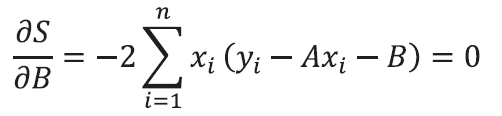
正

正

（以下2021年3月3日更新）

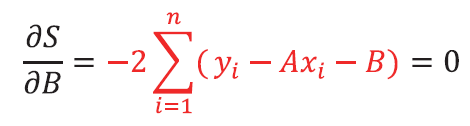
P.29　上から2番目の数式

誤

誤

正

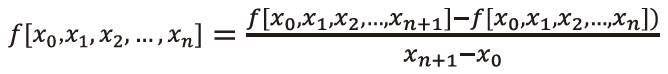
正

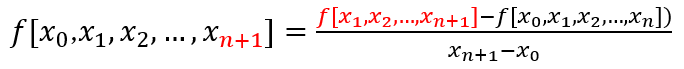
P.29　下から1番目の数式

誤

誤

正

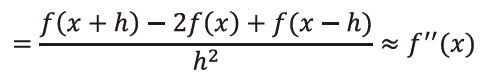
正

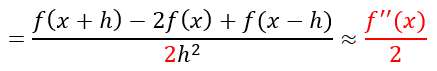
P.92　下から1番目の数式

誤

誤

正

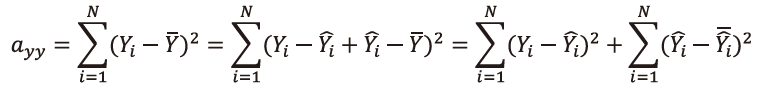
正

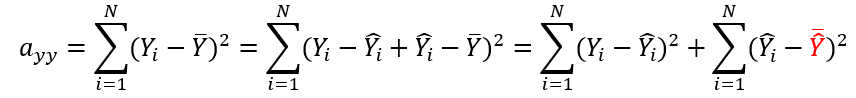
P.93　上から2番目の数式

誤

誤

正

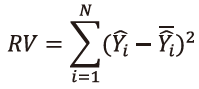
正

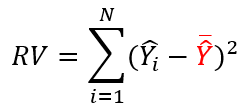
P.93　表4-2 回帰変動の平方和

誤

誤

正

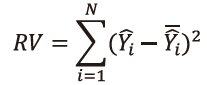
正

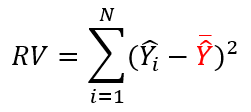
P.94　上から2番目の数式

誤

誤

正

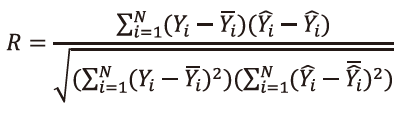
正

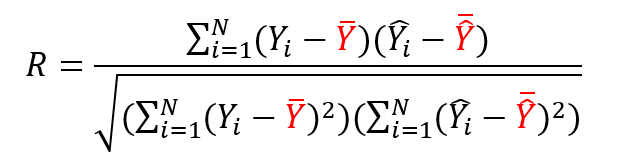
P.94　上から3番目の数式

誤

誤

正

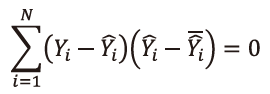
正

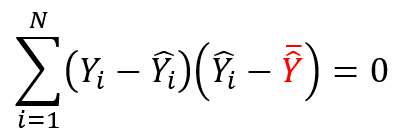
P.95　上から1番目の数式

誤

誤

正

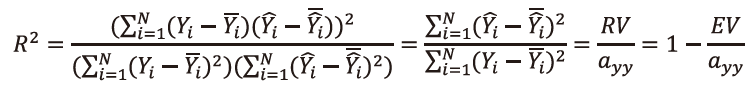
正

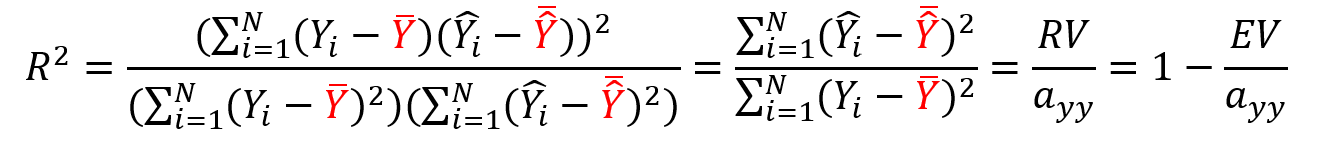
P.180　リスト7-4

誤
# 座標点更新の際に必要なベクトルを計算（逆行列に関しては特異値分解で計算）
dx=svd(A)$u%*%diag(1/svd(A)$d)%*%t(svd(A)$v)%*%(-y)
正
# 座標点更新の際に必要なベクトルを計算
dx=solve(A)%*%(-y)

商品一覧