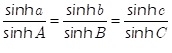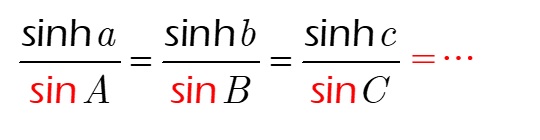概要
ユークリッド幾何学というのは,数学を学ぶときにふだん使っている平面・空間(幾何学)です。それに対して非ユークリッド幾何学があります。これまでに学んできた図形に関する事柄を曲がった世界,非ユークリッド幾何学の観点で見てみるとどうなるか,図と式でわかりやすく解説します。たとえば,高校で学ぶ正弦定理や余弦定理を非ユークリッド幾何学で考えると,驚くべきことにユークリッドで見たときと似たような式が出てくるのです。それは一体何を表しているのでしょうか。双曲幾何学,球面幾何学についても丁寧に解説します。
こんな方におすすめ
- ユークリッド幾何学,非ユークリッド幾何学,双曲幾何学,ポアンカレ予想などに興味がある人
目次
第0章 平行線の公理と幾何学
- 0.1 ユークリッド幾何学について
- 0.2 第5公準と平行線の公理
- 0.3 双曲幾何学について
- 0.4 球面幾何学について
第1章 曲がった世界と直線
- 1.1 ユークリッド幾何学
- COLUMN 直積集合(direct product)
- 1.2 球面幾何学
- 1.3 双曲幾何学
- COLUMN 双曲幾何学と虚数を半径とする円
- COLUMN ミンコフスキー内積と双曲面モデル
第2章 道のりと距離
- 2.1 道のりと距離
- 2.2 ユークリッド平面上の2点間の距離
- 2.3 球面上の2点間の距離
- 2.4 双曲面上の2点間の距離
第3章 角度と内積
- 3.1 2直線のなす角
- 3.2 極座標表示
- 3.3 2点間の距離と内積
第4章 平行移動
- 4.1 ユークリッド平面上の平行移動
- 4.2 球面上の平行移動
- 4.3 双曲面上の平行移動
第5章 正弦定理
- 5.1 ユークリッド三角形の正弦定理
- 5.2 球面三角形の正弦定理
- 5.3 双曲三角形の正弦定理
- 5.4 正弦定理の統一的な表示
第6章 余弦定理
- 6.1 第1余弦定理
- 6.2 第2余弦定理
- 6.3 三平方の定理(ピタゴラスの定理)
- 6.4 まとめ
- 付録A 三角関数とは
- 付録B 球面三角形の面積
- 付録C 正弦関数と余弦関数の一般化
- 付録D その他の定理たち
サポート
正誤表
本書の以下の部分に誤りがありました。ここに訂正するとともに,ご迷惑をおかけしたことを深くお詫び申し上げます。
P.174 下から5行目の式
| 誤 |
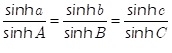
|
|---|
| 正 |
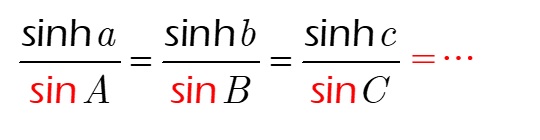
|
|---|