概要
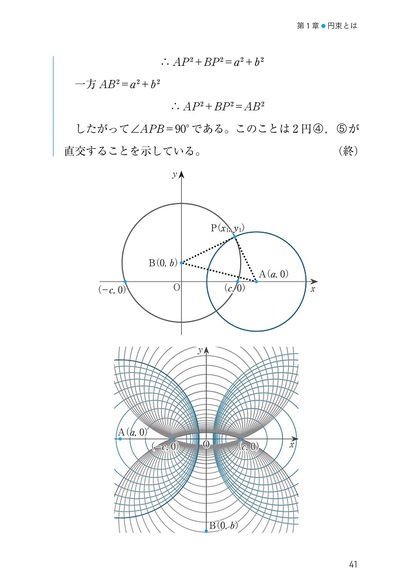
高校のときに学ぶ「図形」と「方程式」。その中で2円の交点を通る図形を求めるために,2円の方程式の差をとるという計算をした覚えはないでしょうか。2円が交わる場合は,その交点を通る直線を表していました。では2円が交わらない場合,差をとって得られる方程式はいったい何を表しているのでしょうか。実は,方程式の差をとって終わりではもったいないほどの深い話が続くのです。
本書では,教科書や参考書とは異なる手法で円を中心にした平面幾何にアプローチし,さらに虚点,虚円,虚接線にまで話を広げて,「円束」を易しく丁寧に解説します。
円と円,円と直線,直線と直線など「幾何」の部分と方程式やパラメータといった「代数」の部分のアイディアが詰まった「円束」を考えると,双方の面白さも味わってもらえるはずです。
こんな方におすすめ
- 図形と方程式,平面幾何といった,幾何に興味がある人
- 複素数の図形的な意味を知りたい人
目次
第1章 円束とは
第2章 反転・極と極線
- 1 反転
- 2 極と極線
- 3 調和点列
- 複比
- 調和点列
- パスカルの定理・ブリアンションの定理
第3章 円束の構成
- 1 基本円束からの構成
- 無限遠点・無限遠直線
- 基本円束
- 楕円的円束の構成
- 放物的円束の構成
- 双曲的円束の構成1
- 双曲的円束の構成2
- 2 1次分数変換と円束
- 1次分数変換
- 1次分数変換の不動点による円束の構成
- 双曲型
- 楕円型
- 放物型
第4章 虚点の視覚化について
- 1 根軸についての再考
- 2 極と極線についての再考
- おわりに
- 参考文献・参考URL
- 索引
- 著者プロフィール
サポート
正誤表
本書の以下の部分に誤りがありました。ここに訂正するとともに,ご迷惑をおかけしたことを深くお詫び申し上げます。
P.10 下から6行目
P.12 図の差し替え
| 誤 |
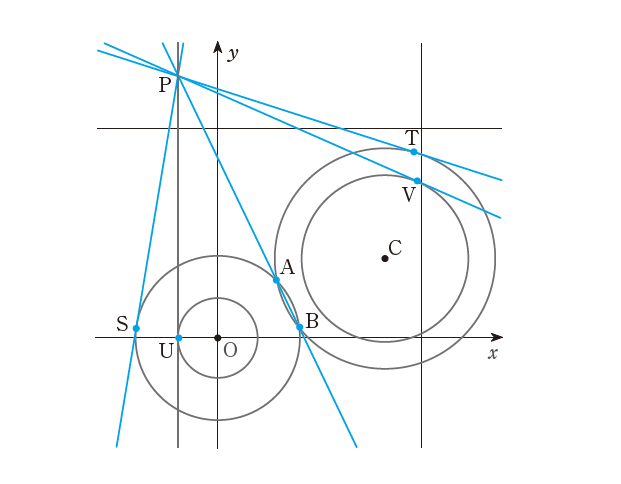
|
|---|
| 正 |
※右側の小さい円はx軸に接しています。
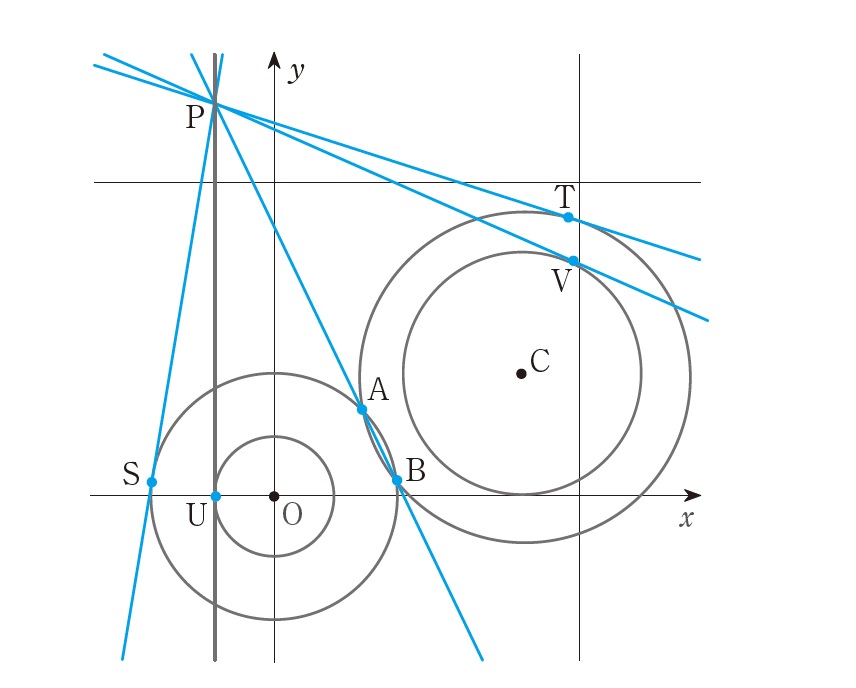
|
|---|