前回に続いて、モンティ・ホールの問題について考える。問題は次の通りだった。

3つの箱があり、1つに賞品が入っていて、残り２つは空箱である。解答者が1つの箱を選ぶと、どの箱が当たりか知っている出題者が、残った2つの箱のうち空箱を開けて見せ、箱を取り換えてもいいという。取り換えたほうがいいだろうか。

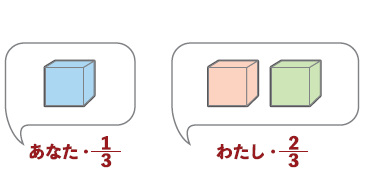
答えは「取り換えた方がいい⁠」⁠。取り換えると当たる確率は2/3に増える。多くの人が、残った箱は２つ、どちらかが当たりなのだから、当たる確率はいずれにしても1/2でうっかり出題者の口車に乗らなくても当たる確率は同じで1/2だ、と考える。しかしこれは間違い。これはこう考えると分かりやすい。解答者が1つの箱を選び、出題者は残った2つの箱を選んだと考えるのである。もちろん出題者は2つの箱を選んだのだから、当たる確率は解答者の2倍である。ただし、出題者の選んだ2つの箱のうち片方は空箱なのだが、そのことは最初から解答者にも分かっているのだから、出題者が空箱であることを知っている片方の箱を開けても開けなくても、確率に影響は与えない。したがって、解答者の当たる確率は1/3、出題者の当たる確率は2/3である。

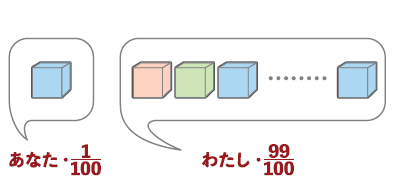
この問題はうまくできている。箱の数3が微妙に効果的なのだ。これを100個の箱にしてみるとよく分かる。解答者は1つの箱を選び、出題者は残りの99箱を選ぶ。そのうち98箱は空箱で、それは事前に解答者も知っているし、出題者はどれが空箱なのかも知っている。出題者が空箱98個を開けて見せると解答者の当たる確率は1/2に上がったか？ そんなことはない、出題者が箱を開けようが開けまいが、解答者の当たる確率は1/100のままで、残った箱に当たりがある確率は99/100である。箱の数が3個だと、それが巧みにカバーされているのである。