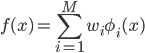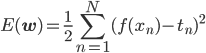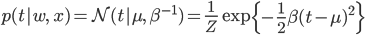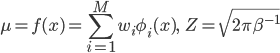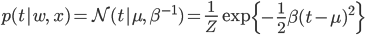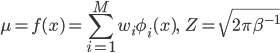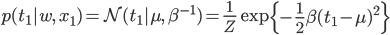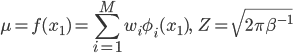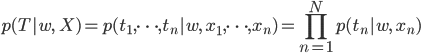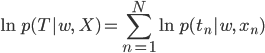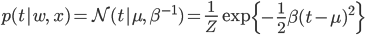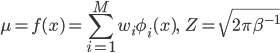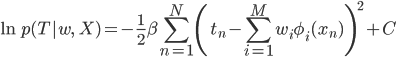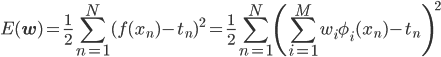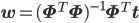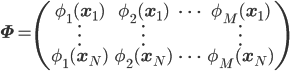今回と次回でいよいよ「ベイズ線形回帰」を紹介します。だいぶ機械学習らしくなってきます。
「ベイズ線形回帰」とは、「線形回帰」(連載第8回、9回、11回)を「ベイジアン」(第10回)の考え方のもとで解くお話です。
さて、復習を兼ねて必要な準備から入っていきましょう。
線形回帰を確率の問題に
「回帰」とは、一言で言えば「データ点から関数を求める方法」でした。
しかし、漠然と「関数を求める」と言われても何をしたらいいかわかりません。そこで「線形回帰」では、あらかじめベースとなる関数φi(x)(基底関数)を用意して、その線形和の範囲から一番適した関数を探すというアプローチをとります。
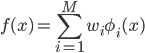
これなら係数wiを決めるだけで関数f(x)を求められますから、するべきことがわかりやすくなりました。
それでは、この係数はどのように決めたらよいでしょうか。もちろん一番いいwiになるようにしたいところですが、何をもって「一番いい」と判断するかの基準が問題です。
前回までの線形回帰では、「一番いい」=「二乗誤差(下式)を最小にするもの」という基準を使っていました。
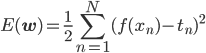
これはこれで実用的ですが、ベイジアンにするにはちょっと困ります。確率の問題になっていないからです。
そこで、線形回帰を確率の問題に読み替えることをしましょう。このとき、「一番いい」の基準が自然に「確率の一番高いヤツ」になるというメリットもあるのですが、詳しいことは後で見ていきます。
天下りになりますが、まずは次のような分布を導入してみます。
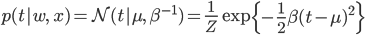 ただし
ただし 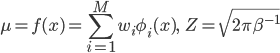
p(t|w,x)は「wとxに依存するtの分布」を表しています。
N(μ,β-1)は、平均がμ=f(x)で、分散がβ-1であるような正規分布(連載第4回、5回参照)を表す記号で、釣鐘型と呼ばれる下図のような形の分布になります。
正規分布N(0,1)のグラフ
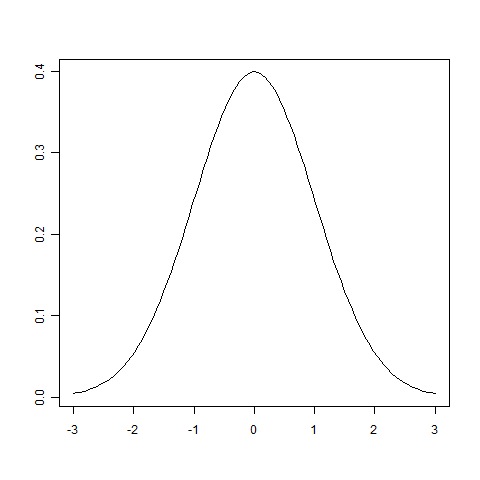
ここで初めて出てきたβは「ノイズの精度」と呼ばれる値で、得られるデータがどのくらい「真の値」からぶれていてもいいかを指定するパラメータになります。詳細は次の項で説明します。
この分布p(t|w,x)を導入さえすれば、あとは確率の道具だけを使って線形回帰が解けてしまうのですが、その前に「この降って湧いた分布p(t|w,x)って何?」というところが気になりますよね。先にその疑問をかたづけてしまいましょう。
ノイズ=確率分布
線形回帰のお話の中で、回帰によって得られる関数の値f(x)=Σwiφi(x)は、データ点を必ずしも通らないことを見てもらいました。無理にデータ点をすべてぴったり通そうとする「過学習」と呼ばれるような問題を起こすこともあるのでしたね。
これは観測されたデータ点が必ずしも「正確な値」ではないことを反映しています。
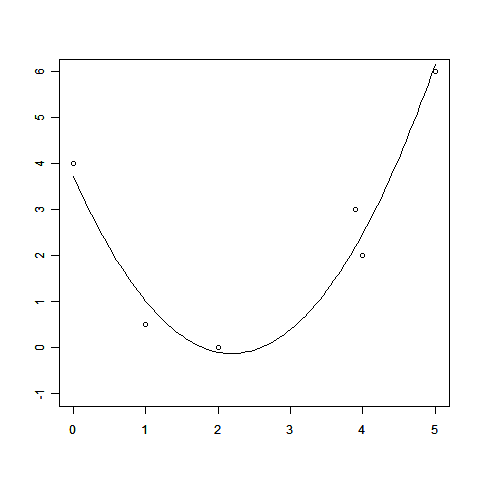
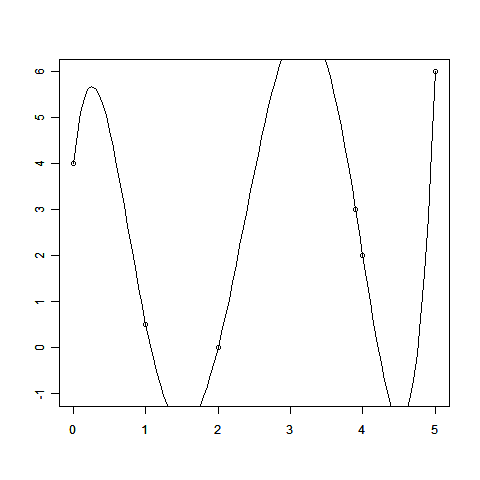
このとき、「少しずれているけど、もともとのデータのせいだから許してね」と謝るだけで話が済む場合は楽なのですが、現実の問題はそう簡単には許してくれません。
「データはもともとどれくらいずれてたの? 新しいデータがどれくらいずれるのかも見積もってね」とか、「ずれてもいいけど、全体でこれくらいに抑えて欲しい」とか、突っ込まれてしまうことになります。
このような課題に対応すべく、「ずれ具合」を定式化する必要に迫られます。色々な方法が考えられるでしょうが、「観測されたデータには、あるランダムなノイズが足されている」という考え方がとても便利でよく使われています。
ランダムと言っても、気分次第であっち行ったりこっち行ったりする「本当にデタラメ」ではさすがに手に追えません。やはり予測値に近いと確率が高くて、離れるほど確率が低くなる、そういう分布に従うくらいのことは仮定したいものです。
そんな「中心に近いほど高く、離れるほど低い分布」で何かいいものはないでしょうか。
ん? ついさっきそういう分布を見たような気がしませんか? そう、正規分布はまさにその条件にぴったり。こういった背景を念頭に置いて、先ほど導入した分布をもう一度眺めてみましょう。
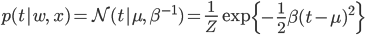 ただし
ただし 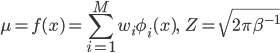
N(μ,β-1)は、予測値μ=f(x)を中心に、離れるほど確率が低くなる分布です。その低くなり具合はβによってコントロールされていて、βが大きいと中心に強く集まり、小さいとずれも幅広くなります。そのため、分散の逆数であるこのβは「精度」とも呼ばれています。
こうして、ずれ具合を正規分布を使って定式化できるようになりました。しかも、今回詳しいことは省略しますが、正規分布には計算が楽になるという嬉しい特典がこっそり付いていますので、願ったりかなったりというわけです。
ちなみに、こうした「観測値のずれ具合を正規分布に従うノイズで説明する」研究をしていたもっとも有名な人がガウスさんです。おかげで正規分布はガウス分布とも呼ばれるようになりました。
確率版の線形回帰を解く
それでは導入したp(t|w,x)を使って線形回帰が解けるかどうか見ていきましょう。
まずはデータ点が1個(x1,t1)だけの場合で考えてみます。このデータをp(t|w,x)に代入すると、「この点を取り得る確率」が求められます。
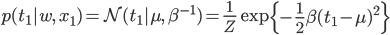 ただし
ただし 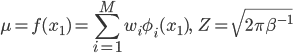
式と値があったので代入してみましたが、このp(t1|w,x1)とは一体何者でしょう?
p(t1|w,x1)という形を見ると、ついt1が動くような気がしてしまいますが、(x1,t1)は観測済みのデータ点なので、どちらも勝手に動かすわけにはいきません。
一方wは「まだわかっていない、これから最適な値を定めたいパラメータ」なので、動かしてみることができます。するとこのp(t1|w,x1)はwの関数とみなすことができます。
機械学習ではその「wの関数p(t1|w,x1)」を「尤度関数」と呼びます。
この連載に「尤度(ゆうど)」という言葉が出てくるのは初めてですね。「尤度」とは、一言で言えば「観測データがとりうる確率」です。
「それってただの『確率』だよね? なんかわざわざ変に小難しい名前だし……はっ。これは理解がおぼつかない人間を煙に巻いて、振り落とす作戦!?」とか思われるかもしれません(笑)。まあ不必要に小難しい用語であることは認めますが、決して嫌がらせのためにあるわけではなく、むしろ「尤度」というのは、確率を使って問題を解くためのとてもおもしろい考え方なのです。
もう少し具体的に説明しましょう。
「確率」というと普通は「あるサイコロをもし振ったら、1が出る確率」のように、これから起きる可能性のあること(事象)それぞれがどれくらいの割合で起きるのかを表します。
一方「尤度」というときは、「すでに観測されている、起きてしまったデータ」の確率を考えています。
つまり、候補となるサイコロがいくつかあるような状態で、「サイコロのどれかを振ったら1が出た。さて、どのサイコロを振ったのか?」という問題を、それぞれの1の出る確率を比べることで決める。それが「最尤推定」という考え方になります。
これが線形回帰だとどういうことになるのか考えてみましょう。
わかりやすくするために、今候補となるパラメータはwAとwBの2通りに限られているとします。そしてパラメータそれぞれごとに「尤度」は求められますが、それらの間にp(t1|wA,x1)>p(t1|wB,x1)という大小関係があったとしましょう。
このとき「尤度」の大きいwAの方が、今実際に起きているデータが発生しやすいわけですから、パラメータとしてより適していると見なすのです。
こうして確率版の線形回帰では、尤度関数(wの関数でしたね!)を最大にするwが最適なパラメータとして選ばれます。
p(t1|w,x1)がデータ(x1,t1)を説明する尤度関数であることには納得できましたが、しかし実際にはデータはもっとたくさんあります。N個のデータ点X=(x1,……,xN),T=(t1,……,tN)に対しても、その起きる確率を考えてみます。
実は簡単に求めることができます。各データ点についての尤度を全て掛け算すればいいのです。サイコロを続けて振ったときの出た目の確率は、それぞれの目の確率の掛け算になっていたことを思い出してもらえばわかりやすいでしょう。
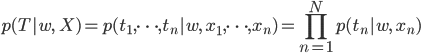
掛け算より足し算の方がやさしいので、この両辺の対数をとったものを扱うことが多いです。これを対数尤度関数と呼びます。
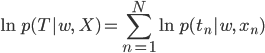
対数はlogと書く方が馴染みある人の方が多いでしょうが、ここでは機械学習の作法にならってlnと書くことにします。自然対数の底を用いる場合はlnを、2や10を底とする場合はlogを使うことが多いようです。
対数関数は単調増加(右肩上がり)なので、対数をとる前に最大となるwと、対数をとった後に最大となるwは一致します。ですから、より簡単な対数尤度関数を最大化するwを求めればよいことになります。
対数が出て来て余計難しいと思うかもしれませんが、今回は本当に簡単な式になることをこれからちゃんと確認しましょう。
それぞれのp(t|w,x)は次のような形をした正規分布でした。
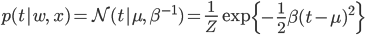 ただし
ただし 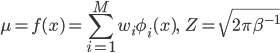
この対数をとると、expの中身はそのまま出てきて、これはwに注目するとただの二次関数です。
expの前についている1/Zにはlnが付きますが、よく見るとそもそもwが含まれていないため、対数尤度関数(wの関数!)の中ではただの定数扱いになります。
さらに目的が「関数を最大化するwを見つける」だったことを考えると、その定数項は求める必要すらないことがわかります。
そこで定数項をCという記号でまとめてしまえば、対数尤度関数は次のような形に整理できます。
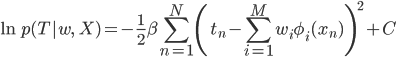
元の尤度関数が「ややこしい正規分布の式をさらに掛け算しまくったもの」だったことを考えると、ずいぶん簡単になってくれましたよね? まあこの式が簡単かどうかはおいといて(!)、どこかで見たことのあるような式だなあ、と気づけたならなかなか鋭いです。
実は第9回に出てきた、線形回帰を最小二乗法で解く場合の二乗誤差の式にそっくりなのです。二乗誤差の式を引用しますので、見比べてみましょう。
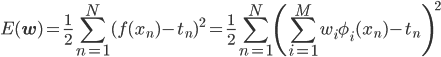
すると、二乗誤差に負符号とβと定数項Cを付ければ対数尤度関数になることがわかります。括弧の中身の引き算が逆ですが、二乗しているから同じですね。
符号が逆なのは、二乗誤差は「最小化」、対数尤度関数は「最大化」しようとしていることに対応します。そしてβ(>0)やCは最小だの最大だのを与えるwには何の影響もありません。
したがって、確率化した線形回帰では、最小二乗法による線形回帰と全く同じ答えが得られます。
そこで、最後に第11回で紹介した最適なwを求める式を引用しておきましょう。
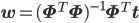 ただし
ただし 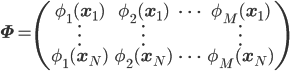
まとめ
同じ結果になるということは、なんだか複雑なことをしてわざわざ確率化しても無駄だったってこと?と感じてしまったかもしれませんね。でもご心配なく。
そもそも最小二乗法にしても、確率的な線形回帰にしても、何を最適さの基準とするかは「仮定」でしかありません(第8回でその話をうるさいくらいしましたね)。
しかし今回「全く異なる仮定を入れたのに同じ結果が導かれた」ことには、それらの仮定の選び方にある種の妥当性を与えてくれるという意味があります。また、確率化はベイズ化のためにどうしても必要なステップでもあります。
そこで次回は、この確率化した線形回帰をさらにベイズ化していきます。