お詫びと訂正（正誤表）

弊社発売の「理系のためのVisualBasic 6.0 実践入門」におきまして，現在までに，以下に示しますような誤り・訂正事項がありました。この場をお借りいたまして，本書をお買い上げいただいた読者の方々や関係者に書籍の内容に誤りのあったことを深くお詫びいたします。 （Last update:2005/07/22）

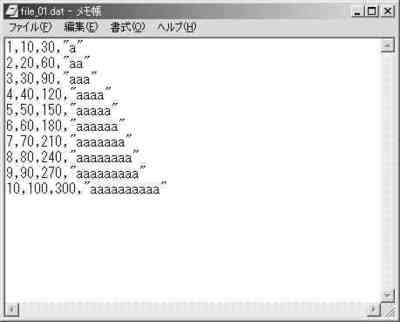
P.132　図2.8.2を変更

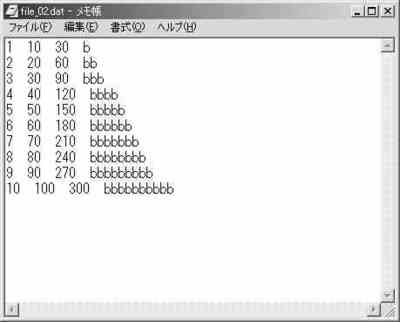
P.135　図2.8.4を変更

P.166　うるう年の定義（一番下のリストの上の段落中）

誤	うるう年の定義をそのまま，If～Then構文による条件判断で実現します．すなわち，もし4で割り切れなければうるう年でない．割り切れた場合，もし100で割れて400でも割り切れたらうるう年，さもなくば（すなわち，100で割れて400で割れなければ）うるう年でない，さもなくば（すなわち，4で割れて，400で割れたら）うるう年です．これをそのままコード化します．例を以下に示します．
正	うるう年の定義をそのまま，If～Then構文による条件判断で実現します．すなわち，もし4で割り切れなければうるう年でない（平年）．割り切れた場合，もし100で割り切れて，400で割り切れない年は平年，さもなくば（すなわち，100で割り切れて400でも割り切れれば）うるう年，さもなくば（すなわち，4で割り切れて，100で割り切れなかったら）うるう年です．これをそのままコード化します．例を以下に示します．

P.167　リストLeap1.vbp（一番最後から３行目のendifが２つ続いているところの前に追加）

P.58

誤	（1）7.333…　（2）10.6666…　（3）9.1875 （4）3.1666…
正	（1）7.333…　（2）10 （3）9.1875 （4）3.1666…

P.114　リスト下から５行目

誤	t = y.Im ^ 2 + y.Im ^ 2
正	t = y.Re ^ 2 + y.Im ^ 2

P.272　２行目　arctanの式

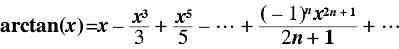
P.278　上から８行目

誤	処理なので，10のべきとしては 2^1023=308.2 までの値を表すということです．
正	処理なので，10のべきとしては 2^1024=308.2 までの値を表すということです．

P.278　中央色つき部分

誤	1023 8.98846567431158E+308
正	1023 8.98846567431158E+307

P.278　（注）の段落の最後

誤	上の値の2倍の1.79769313486232E+309が上限とされています．
正	上の値の2倍の1.79769313486232E+308が上限とされています．

P.331　リスト7.4.1 FFTによる周波数の計算　中

id= 1.0 FFTの計算

id=-1.0 逆FFTの計算

の部分が逆でした。正確には，

id=-1.0 FFTの計算

id= 1.0 逆FFTの計算>

になります。次のページの下側の注の部分も逆になります。

P.363　最初の連立方程式の一番下

誤	2ｘ1 ＋ 2ｘ2 － 5ｘ3 = 2
正	2ｘ1 － 2ｘ2 ＋ 5ｘ3 = 2

P.363　４番目の連立方程式の一番上

誤	ｘ1 － 0.2ｘ2 ＋ 0.3ｘ3 = 1.6
正	ｘ1 － 0.2ｘ2 ＋ 0.2ｘ3 = 1.6

P.418　リスト11.3.2　キャプション中

誤	（\Source\Chas11\Fermat.vbp(frmFermatTest.frm)）
正	（\Source\Chap11\Fermat.vbp(frmFermatTest.frm)）

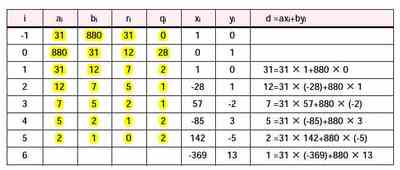
P460の表（１刷）

P.461下から5行目（1刷，2刷）

誤	秘密鍵は，ed=1 (mod m)となる(d,m)の値でした．上の式と同じ形です．よって，exi+myi=1 を満たすxiが秘密鍵のdということになります．
正	秘密鍵は，ed=1 (mod φ(m))となる(d,m)の値でした．上の式と同じ形です．よって，exi+φ(m)yi=1 を満たすxiが秘密鍵のdということになります．