微分方程式は、工業・産業、経済、生物学などあらゆる分野で、現象を表したり、変化率を考えたりするときに用いられます。それを解く方法として、変数分離形微分方程式の解法、同次形微分方程式の解法、定数係数2階同次線形微分方程式の解法などがあります。また単に解を求めるだけではなく、解が明示的なのか、特殊なのかといったことも工学で利用する上では重要なポイントです。
本書では、工業分野で利用する微分方程式に焦点を当てます。例えば、微分方程式は物体の運動を記述したり、電気回路を考えたりするときに大活躍します。本書で取り上げている例をいくつかご紹介します。
基本的な微分方程式の例
まず最初は、みなさんが必ず一度は学ぶ自由落下運動です。
図 第1章 自由落下運動
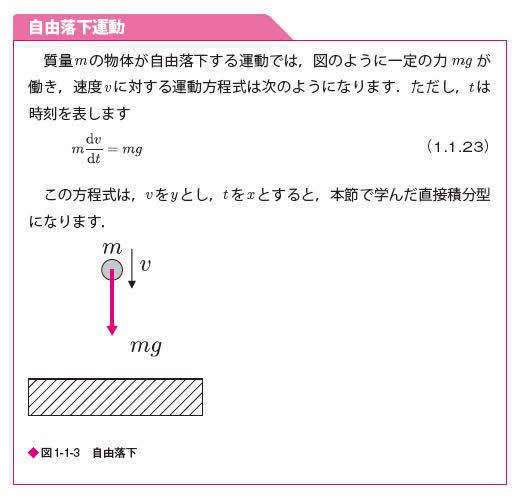
ニュートンの運動法則も2階微分方程式で表現されます。
次に挙げるコイルと抵抗の回路も微分方程式を満たします。
図 第1章 コイルと抵抗

本書ではこのような基礎からわかりやすく解説しています。
微分方程式をとくコツがわかる
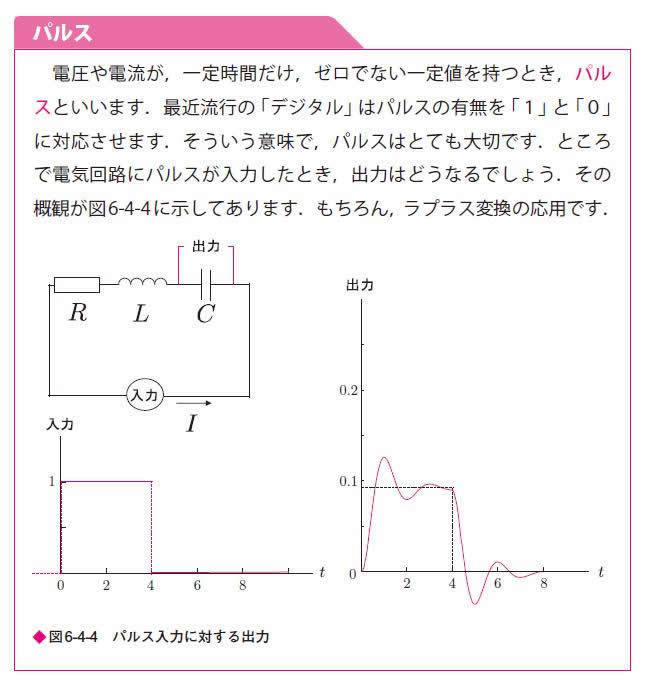
微分方程式を解く道具として、ラプラス変換もあります。ラプラス変換を用いると、微分を含まないシンプルな式になるケースがあります。そして逆ラプラス変換により、微分方程式の解を求めるのです。
図 第6章 パルス
さらに発展へ
地震や振動なども微分方程式のシミュレーションが役立っています。地震波の生成や伝播のシミュレーションもまたしかりです。微分方程式は私たちの安全な暮らしにも一役かっているのです。
微分方程式は量子力学や素粒子物理などを理解するうえでも重要で、ヤン・ミルズ方程式(ベクトル場を未知関数とする偏微分方程式)、ソリトン方程式(偏微分方程式)、パンルヴェ方程式(非線形常微分方程式)、複素領域の線形微分方程式へとつながっていきます。
図 練習問題5-14
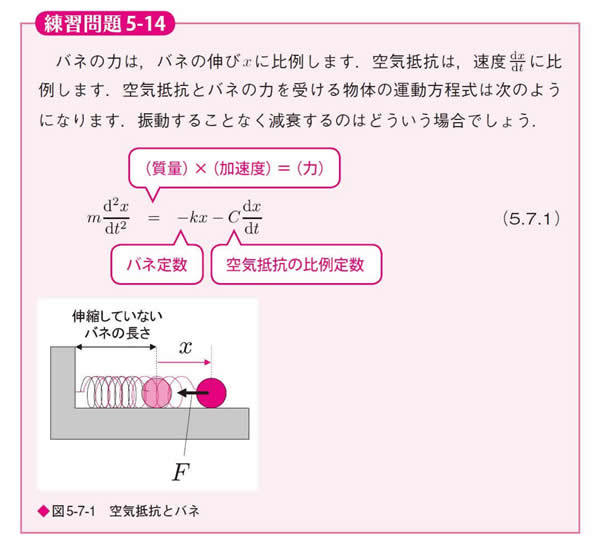 図 練習問題5-14 解答
図 練習問題5-14 解答





