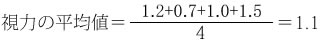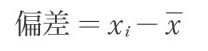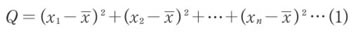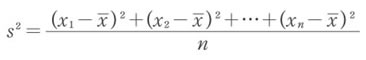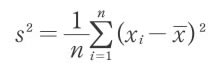統計学には、大きく分けて二つの分野があります。記述統計学と推測統計学です。記述統計学は資料を整理し系統立てる方法を研究します。推測統計学は資料を全体の一部と考え、その資料から全体についての情報を得る方法を研究します。
資料の視覚化
記述統計学の大きな目的の一つは、資料を視覚化し、資料の本質を直感的に理解できるようにすることです。この統計資料の視覚化には様々な形態があります。代表的なものとしては、円グラフや棒グラフ、折れ線グラフがあります。変わったところでは、株価変動を示すローソク足チャートも、記述統計学の対象になります。他にもユニークな統計資料の視覚化がいろいろと工夫されています。
資料の数値化
グラフ化する以外に、統計資料を理解させるもう一つの方法があります。それは、統計資料を代表的な数値に集約させる方法です。平均値、中央値(メジアン)、最頻値(モード)、分散、標準偏差などが、その代表的な数値になります。
平均値
平均値とは個々の変量の値の総和をデータ数で割ったものです。利用される分野によって、平均点、平均所得、平均時刻などと名を変えますが、親しみがあるでしょう。たとえば、次の表で、4人の視力の平均値は次のように求められます。
| 名前 | 視力(両眼) |
|---|
| 海のイルカ | 1.2 |
| 森いずみ | 0.7 |
| 原田すみれ | 1.0 |
| 山野太郎 | 1.5 |
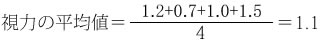
中央値(メジアン)
データを大きさの順に並べたときに、ちょうど中央に位置する値のことを中央値といいます。メジアンとも中位数ともいいます。
たとえば、次の表のように、A~Eの5人の貯蓄高が示されたとしましょう。その中央値は600です。この例の平均値は2000ですが、この資料の場合には、中央値の方が平均値よりも良い代表値になっていると思われます。
| 名前 | 貯蓄額(万円) |
|---|
| Aさん | 200 |
| Bさん | 400 |
| Cさん | 600 |
| Dさん | 800 |
| Eさん | 8000 |
最頻値(モード)
度数分布表において、最も頻度(度数)の高い値のことをいいます。
たとえば、次の表は土地の販売において、価格と区画数の度数分布表です。最頻値は3600万円です。平均値3330万円、中央値3400万円に比べて、この販売資料の最適な代表値は最頻値の3600万円と思われます。
| 価格(万円) | 区画数 |
|---|
| 2800 | 10 |
| 3000 | 15 |
| 3200 | 15 |
| 3400 | 20 |
| 3600 | 40 |
データのバラツキを表す指標
資料を代表する値、すなわち代表値として、平均値、中央値、最頻値を調べました。しかし、代表値だけで資料を語ることはできません。その資料の中のデータの散らばり具合も重要です。というのは、散らばりは標準からのズレ、すなわち各データの個性を表すからです。そこで登場するのが分散と標準偏差です。
偏差
偏差とは個体の値から平均値を引いて得られる値です。たとえば、変量xについて、i番目の個体の持つ値をxiとし、平均値をxとすると、xiの偏差は次のように表わされます。
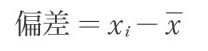
要するに、偏差とは平均値からのズレを表します。
変動
「偏差」は各個体の「個性」を表します。その個性を資料全体で加えあわせれば、その資料の持つ「個性全体」を求めることができます。すなわち、資料の持つ「情報」を表すと考えられるのです。
ところで、個性を表す偏差を単純に加えあわせると、プラスの個性とマイナスの個性が打ち消しあって、値は0になってしまいます。そこで、全体の個性を調べるときには、各々を2乗して加えます。これを変動といいます。また、偏差平方和とも呼びます。通常、Qで表されます。
一般的に次のような資料があるとしましょう。このとき、変動Qは次のように表されます。
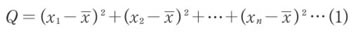
nは個体数、 xは平均値です。
分散
変動Qは資料が大きいほど、値も大きくなってしまいます。ばらつきがなく個性の少ない単調な資料でも、データが増えれば(1)の値Qは大きくなってしまうからです。そこで、個体数nで割ってみましょう。こうすれば、その欠点が避けられます。
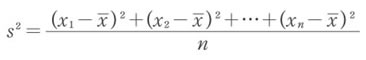
この値を変量xの分散と呼びます。通常s2と記されます。Σ記号を利用すると、次のように表現されます。
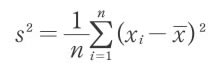
既に調べた平均値と偏差という言葉を利用するなら、分散とは「偏差の2乗平均」と表現できます。
(注)分散は英語でVarianceといいますが、その値は通常js2と表記されます。このsは標準偏差(standard deviation)の頭文字です。この標準偏差の2乗が分散になるのです。