概要

三角関数や微分積分の基本定理など，高校で学びますが，他の数学の分野とどうつながっているのでしょうか。たとえば，微分と積分を結びつけるのが微分積分の基本定理ですが，「心から理解している」人はあまりいません。三角関数，サイン，コサインの波が多項式とどうつながっていくのかを知ると，単に公式を覚えて終わりではもったいないと気が付いてもらえるかもしれません。単元自身の枠を超えた広い視野で眺めてみると本質が見えてきます。カルダノ，ニュートン，オイラー，チェビシェフといった大数学者たちが成し遂げたことは一体何だったのか。代数や解析をこれから本格的に学ぼうとする大学生にも楽しんでもらえます。

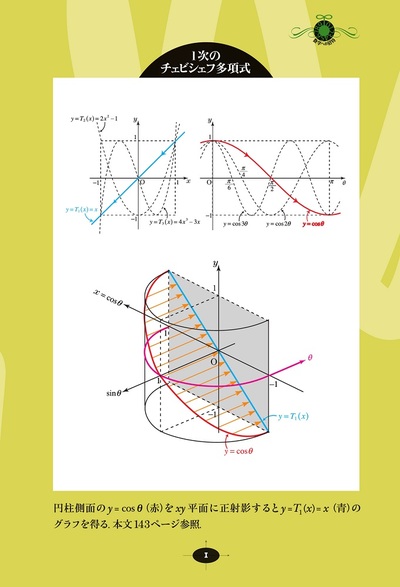
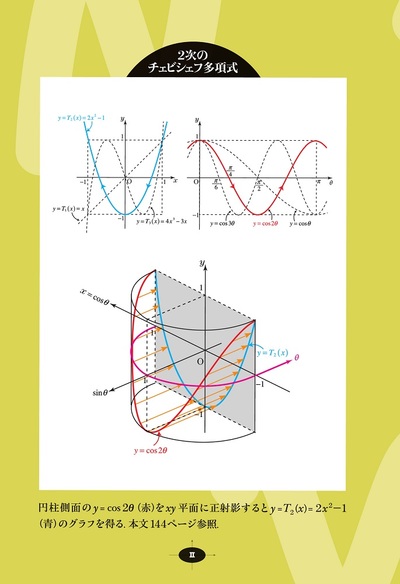
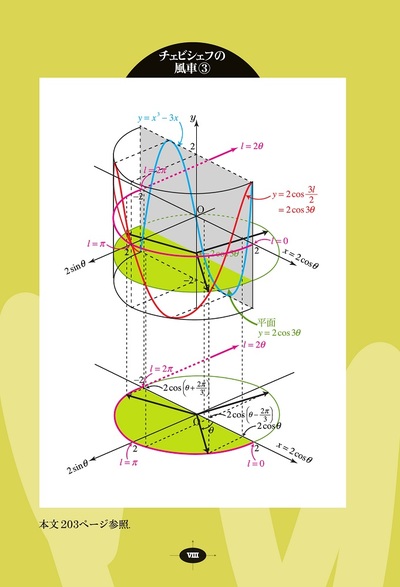
巻頭カラーを設け，グラフと図形を分かり易くご紹介します。

こんな方におすすめ

• 高校以上
• 物理，代数，解析などの繋がりを知りたい人
• 16世紀から19世紀までの数学史に関心がある人など

サンプル

目次

• はじめに
• 【雑談】遊歴算家の歴史について

第１章　3次方程式と三角関数

• 3次式について探究的な学習
• 3次関数のグラフを描いてみる
• 三角関数に置き換えて考える
• 代数的なアプローチ
• カルダノの解法
• 微分法，数列との関わり
• 立方完成という技術
• 社会的知識と数学的知識

第２章　微積分の基本定理

• 差分と微分
• 和分と積分
• 極限と離散化が接続する
• 解像度を上げる区分求積法
• f'(x)dxとは何か
• 微積分の基本定理に至る
• 定積分が面積を表す理由

第３章　バーゼル問題

• 無限小の比較
• 不等式を成長させる
• バーゼル問題
• オイラーのアイデア

第４章　チェビシェフの円柱

• 3次関数のグラフの特徴
• 三角関数の公式の連鎖
• 三角関数の多項式
• 波のグラフと多項式のグラフ
• グラフの振動を追いかける
• かまぼこに巻きつける
• 定性的に理解する
• 後日談

第５章　チェビシェフの風車

• 三角関数の加法定理
• 加法定理から連鎖する公式
• チェビシェフ多項式
• 第二種チェビシェフ多項式
• チェビシェフの円柱に至る
• 3次方程式を再考
• 3次方程式の解の巡回
• チェビシェフの風車

第６章　もう一歩前へ～演習問題

• 【問題３】（5次のチェビシェフ多項式）
• 【問題４】（有理数と無理数）
• 【問題５】（関数の合成）
• 【問題５の改題】
• 【問題６】（カルダノの公式）
• 【問題７】（双曲線関数の加法定理）
• 【問題８】（チェビシェフの円柱Ⅰ）
• 【問題９】（チェビシェフの円柱Ⅱ）
• 【問題10】（正接のn倍角公式）
• 【問題11】（正接を用いた表現）
• 【問題12】（正方形内を振動する多項式）

第７章　競技数学で闘ってみる

• 【問題13】（三角関数の等式）
• 【問題14】（無限個の点集合）

• あとがき
• 著者紹介

サポート

現在サポート情報はありません。