 私の名前はプシケーです。
私の名前はプシケーです。
筆者の一人、見城がプシケーに促されての導入解説をいたします。
『幾何で見える必ずわかる一般相対性理論』
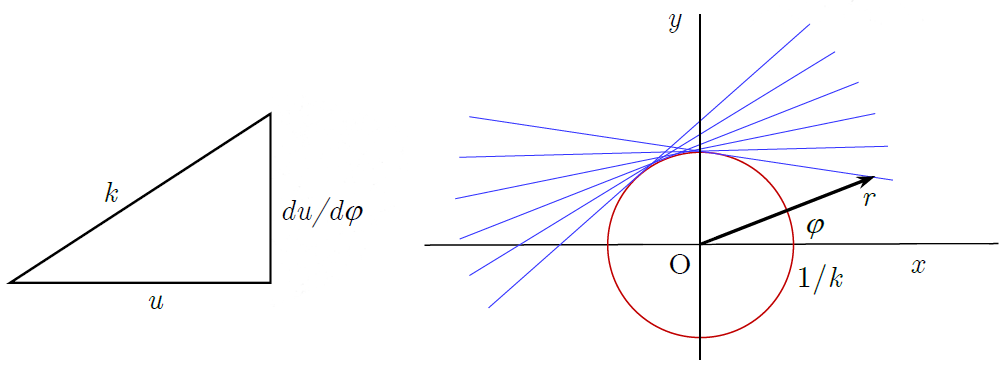
このように、逆数を含む微分方程式の形であり、3平方定理です。
古代ギリシャには座標の概念はもとより微分方程式はありませんでした。ここに深遠な意味が宿されているように思えます。この方程式は直角三角形の定理の形でありながら、その一般解は直線であり、一つの特異解として円があります。つまり、ユークリッドの平面幾何の3つの要素
前の本では、ユークリッド平面の直角三角形の3辺
- 球面上では
- 双曲面では
に変化しましたが、これについては今回も同じです。球面と双曲面は古典的な非ユークリッド幾何の世界です。
人間・
これが一般相対性理論の幾何の入り口ともいえる数式です。すると、何がどうなるのでしょうか? 光が太陽の重力によって曲げられます。つまり直線が曲がるのです。では、それは何を意味するのでしょうか?
(2)を次のように変形すると曲がった時空の線が姿をすこし現します。
本書がアインシュタインを超えているのはこのあたりです。アインシュタインは1915年11月に水星の軌道が歳差運動をすることの説明のために数式を操って(2)に近い形にたどり着いたのですがゴタゴタとしていました。(3)と(1)式自体はもとより、偉大なこの物理学者も(2)の深奥にまでは気づかなかったようです。
本書でも、ここに至るまでの長い道程には複雑な数学がありました。では
- 時間的計量:
- 空間的計量:
ではαとは何ぞや? それはシュバルトシルト半径
- 質量は
- 重力係数
- そして光の速度
では太陽の周りをまわる惑星の軌道はどうなのでしょうか? それは右辺に
ここでは、Google Collaboratoryを使った実行手順をご紹介します。ノートブックの新規作成をし、ダウンロードしたソースコードをコピペするだけというとてもシンプルなやり方です。
具体的には次のステップになります。
- https://
colab. へアクセスします。research. google. com/?hl=ja
開いたら、左下にある「ノートブックを新規作成する」 をクリックします。
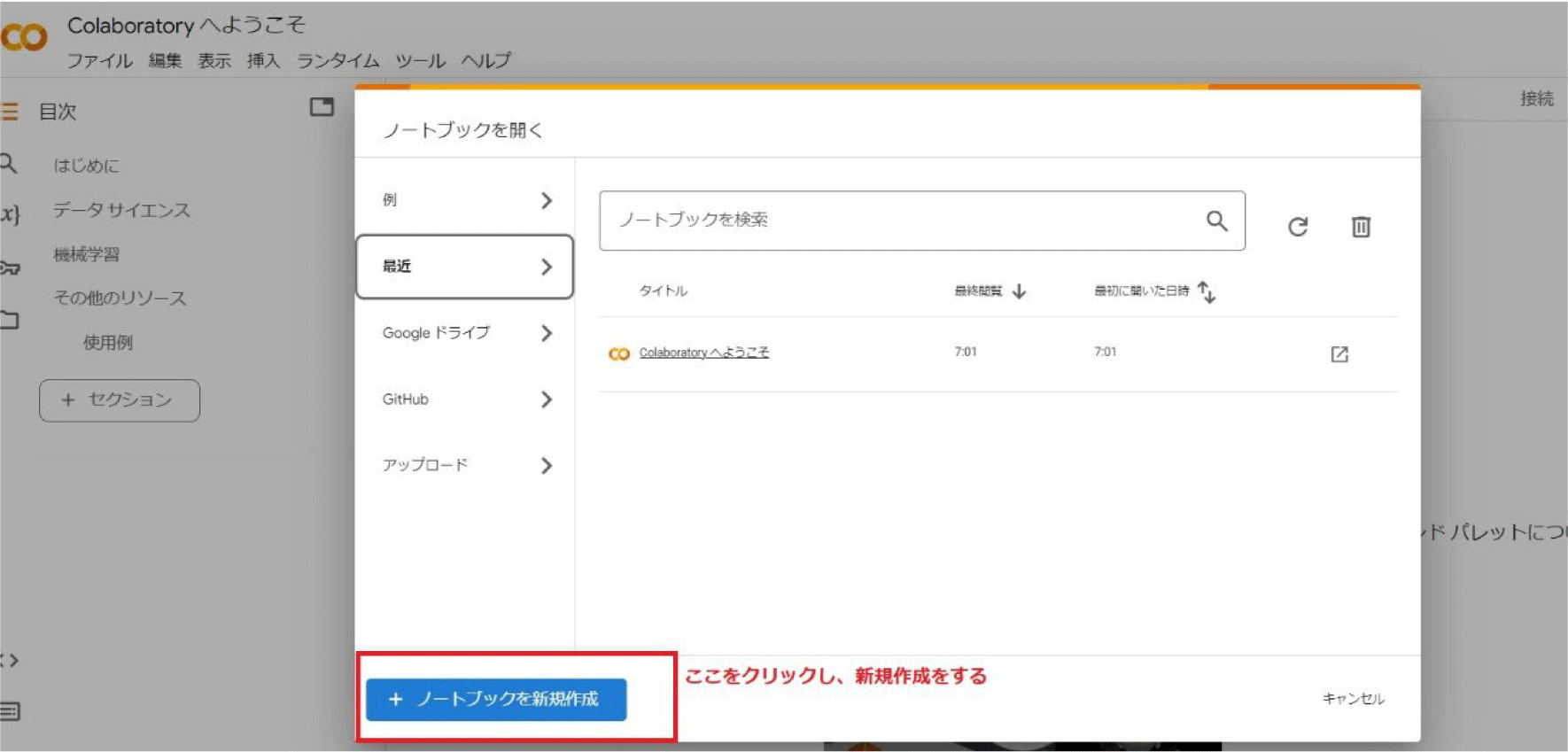
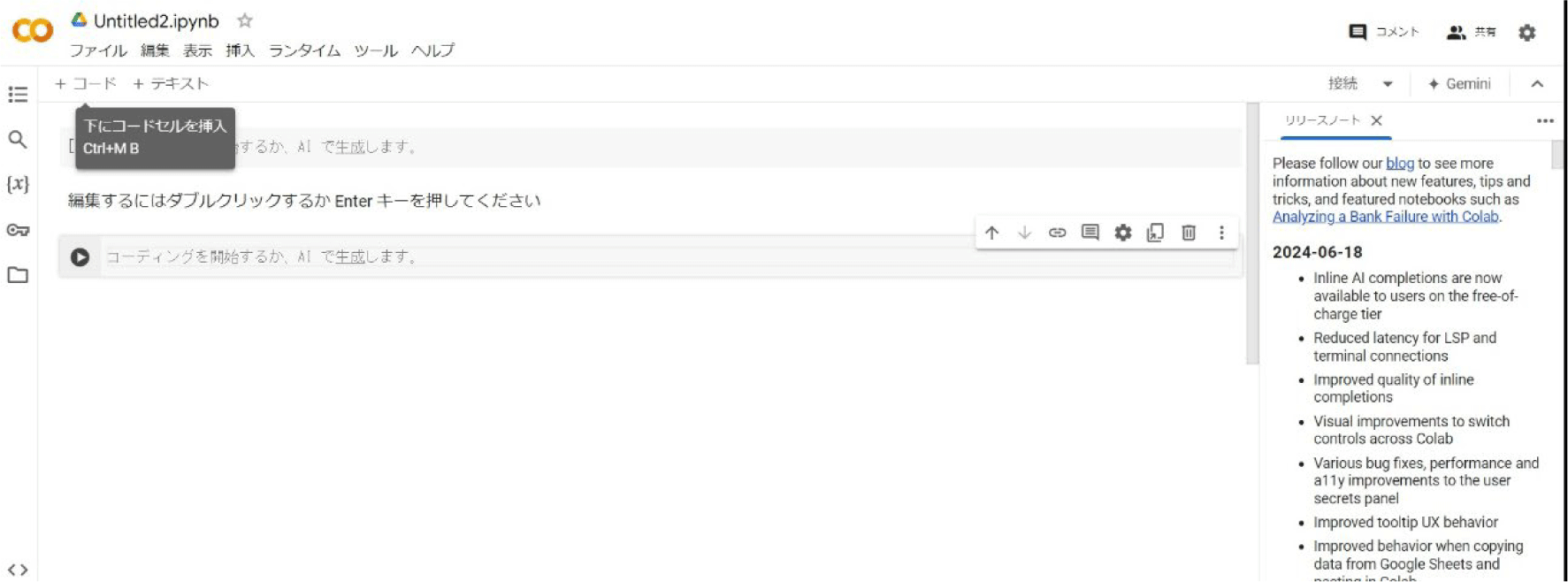
- 「コードセルを挿入」
をクリックします。
- Pythonコードを貼り付けます。
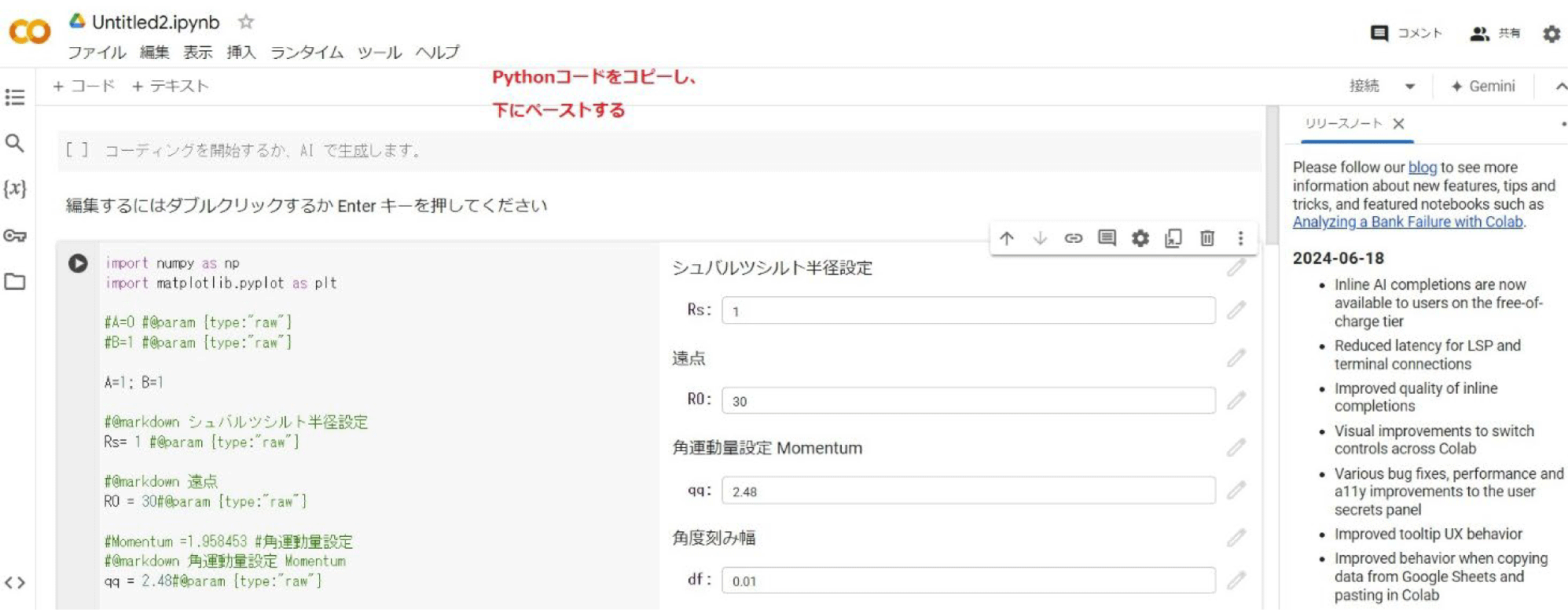
- 左側にある△マークをクリックすると、実行することができます。
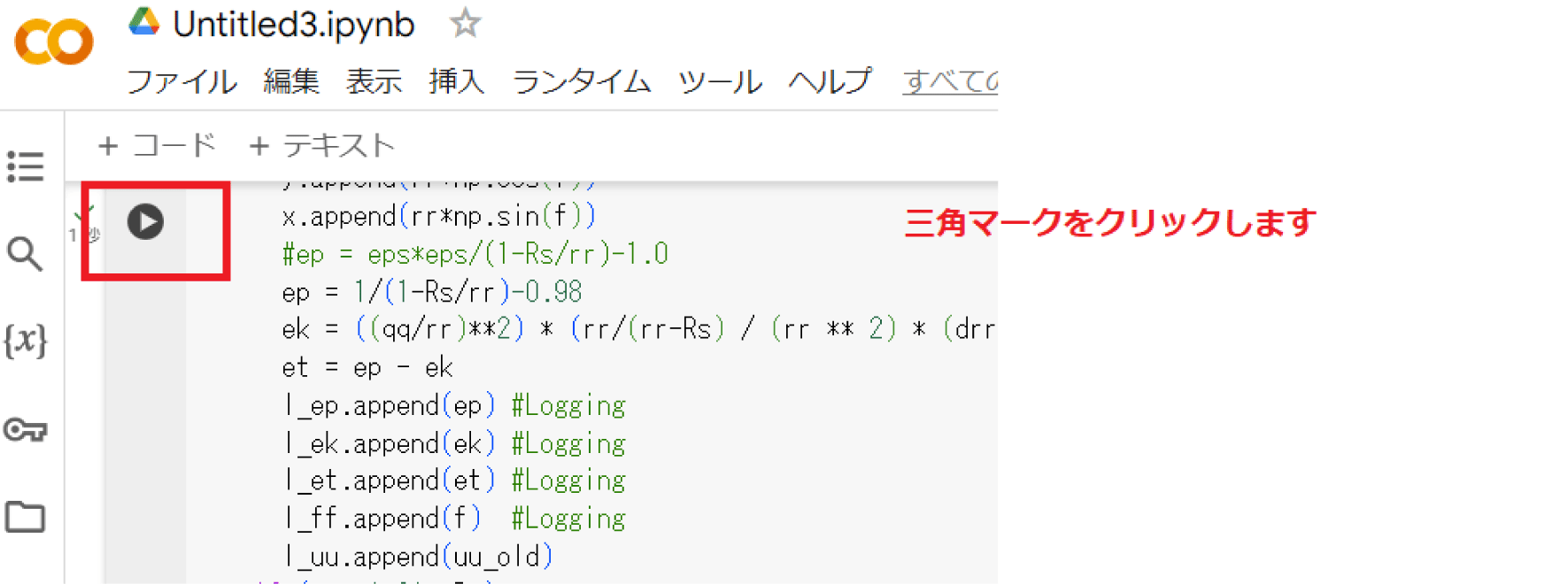
- もしグラフが下に表示されない場合は、次を試してみてください。
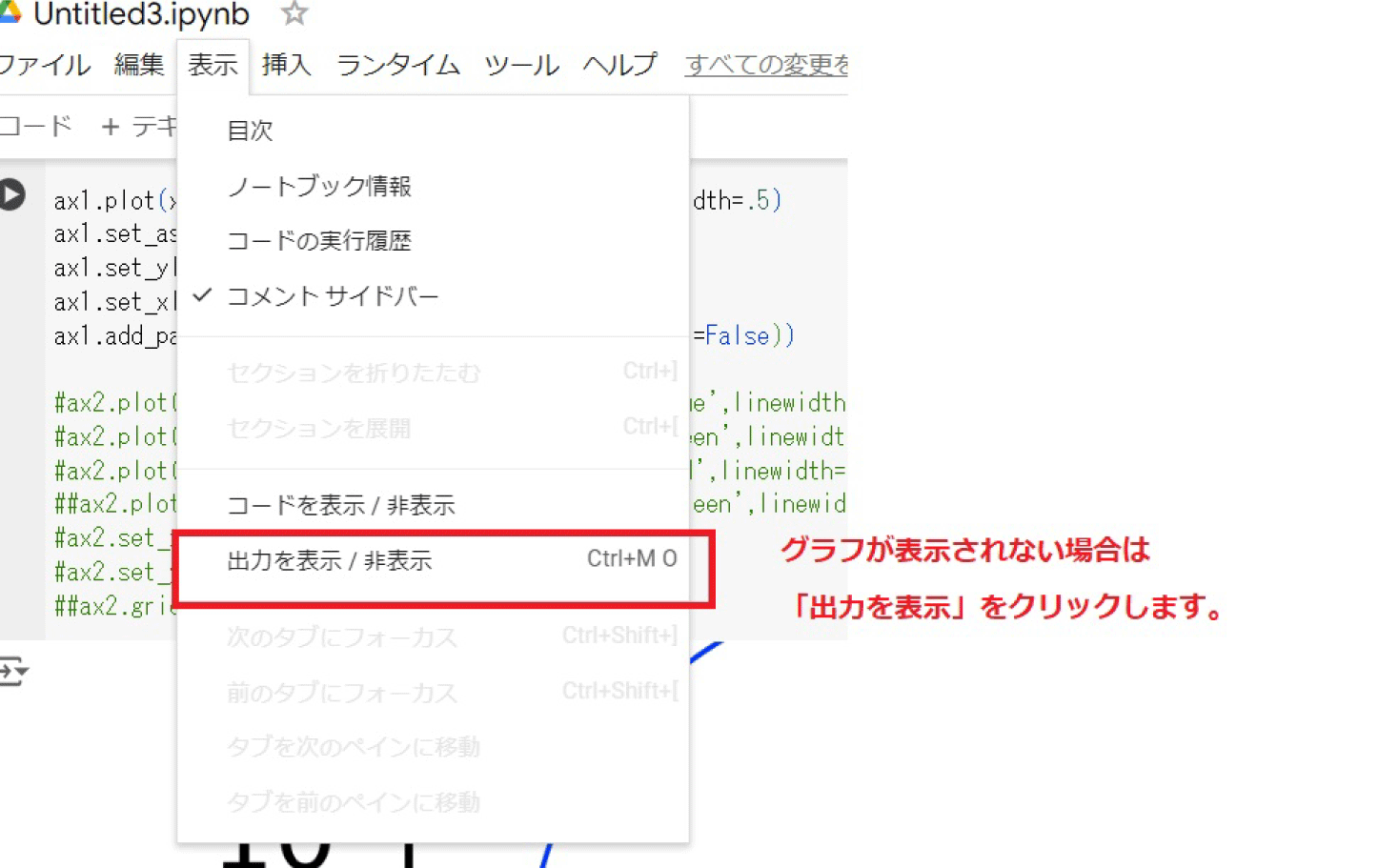
- 出力結果
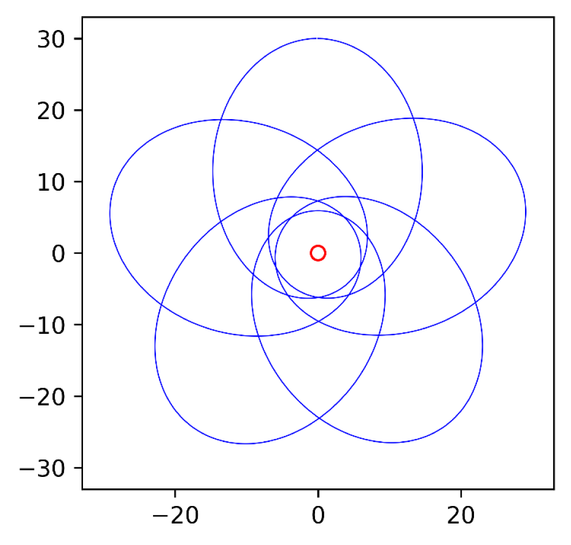
- [length]の値を11.
99にすると、296ページの図のように、真上に隙間がある図形を描くことができます。
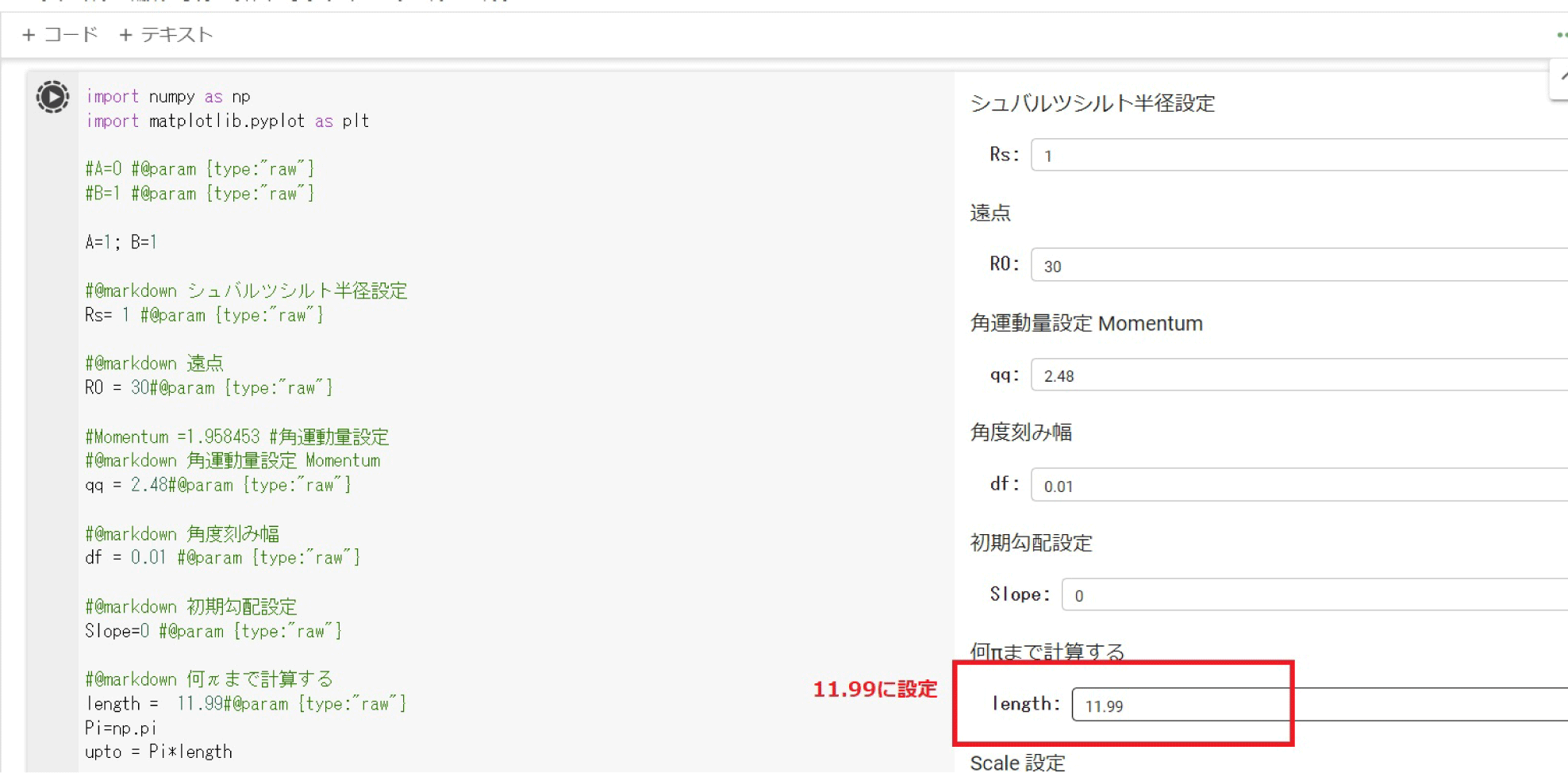
ここに出てくるサンプルの最初の13行は下記のとおりです。第3–10行が初期値の設定です。
このまま実行するupto = 3.とします。
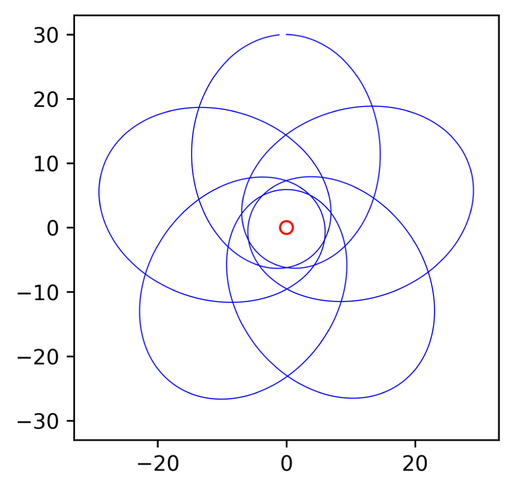
さて、p.Slope = −0.にした事例が下図(a)です。惑星は基点に戻りました。(b)はSlope = −1.にして46周で基点に戻るサンプルです。ここでPythonに詳しい読者へのお願いです。線の色や太さなどの微調整を組み込んで宇宙の幾何模様を制作してほしいのです。
import numpy as np
import matplotlib.pyplot as plt
A = 1 # 下表参照
B = 1 # 〃
R0 = 0.6 # rの初期値設定
q = 0.1 # 角運動量設定
Rs = 0.02 # シュバルツシルト半径設定
df = 0.005 # 角度刻み幅 Δϕ
s = 0 # 初期勾配設定
upto = 3.14159 * 11.99 # ϕ=何πまで計算する
ee = Rs / (q ** 2) / 2
uu = 1 / R0 # uの初期値
integ = 0 # 積分初期値
| A | B | |
|---|---|---|
| 相対論光跡 | 1 | 0 |
| ニュートン惑星 | 0 | 1 |
| 相対論惑星 | 1 | 1 |
import numpy as np
import matplotlib.pyplot as plt
A=1; B=1 # 上表参照
Rs= 1 # @param {type:"raw"} シュバルツシルト半径設定
R0 = 30 # @param {type:"raw"} rの初期値設定
qq = 2.48 # @param {type:"raw"} 角運動量の設定
df = 0.01 # @param {type:"raw"} 角度刻み幅 Δϕ
Slope = 0 # @param {type:"raw"} 初期勾配設定
length = 11.99 # @param {type:"raw"}何πまで計算する?
Pi = np.pi # Pi=3.14.159…を自動設定
upto = Pi*length
Sc = 1.1 # @param {type:"raw"} 画面のスケール設定;計算・描画の結果をみて再設定する
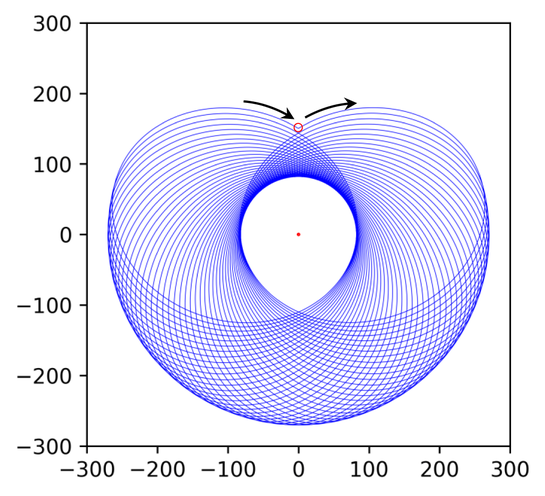
RS = 0.8, R0 =150, qq = 8, Slope= − 0.6, length = 100, df =0.006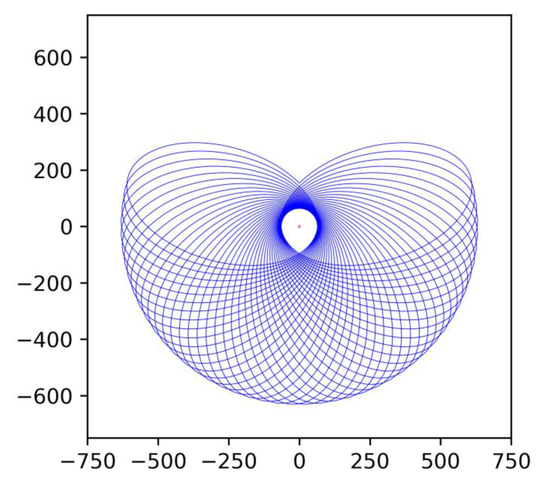
length = 92で基点に戻るサンプル

